Cet article concerne uniquement le schéma en barre multiplicatif “classique”. Depuis juillet 2024 les problèmes de multiplication s’enrichissent d’un nouveau modèle, le schéma cartésien, qui est traité dans un autre article.
Le schéma en barre multiplicatif permet de modéliser des problèmes de multiplication et de division. Sur Actilud, vous trouverez une panoplie d’exercices faisant intervenir différents types de problèmes multiplicatifs. Mais avant de démarrer la résolution de ces problèmes, une petite initiation à la « machine » multiplicative semble nécessaire.
Une démarche possible est de reprendre celle abordée dans mon article sur la schématisation des problèmes additifs. N’oublions pas que le modèle, sur le site, n’est pas une entité abstraite mais bien une « machine virtuelle » que l’on peut manipuler aisément.
L’idéal, dans un premier temps, est donc de présenter l’outil aux élèves avec des indications minimales:
C’est « une machine à résoudre les problèmes ». Trouvez comment elle marche.
Pourquoi peut-on dire que c’est une machine à résoudre les problèmes ?
Quelles sortes de problèmes peut-elle résoudre ?
A disposition des élèves, dans l’idéal : un tableau interactif type TBI, des tablettes ou ordinateurs à disposition pour leur activité de recherche sur le site.
Voyons dans les détails comment la machine fonctionne.
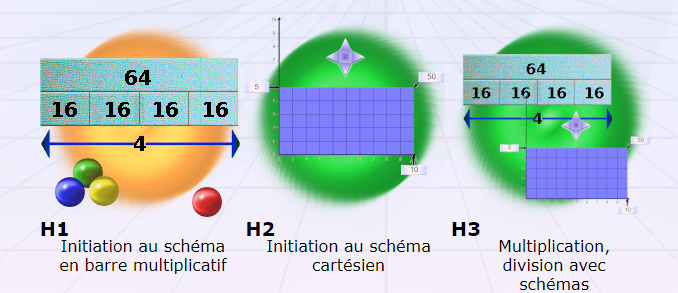
Paramétrage
Dans le menu « Jeu » il y a 3 entrées. La première, « Mode d’emploi », est une présentation animée du fonctionnement de la machine – ce que nous allons aborder ici avec quelques indications pédagogiques en plus.
La seconde entrée, « entraînement – problèmes », permet de se familiariser avec quelques problèmes simples, sachant qu’un panel bien plus complet de problèmes se trouve dans l’exercice H2 : multiplication, division avec schéma.
La troisième entrée, « utilisation libre » nous intéresse ici, car c’est elle qui permet la découverte de la machine dans un premier temps, et ensuite, qui permet le travail sur des problèmes tiers proposés par l’enseignant.
L’entrée « niveau de difficulté », dont le contenu varie selon le jeu choisi, propose deux possibilités, « produit jusqu’à 100 » et « produit jusqu’à 1000 ». Ces entrées permettent donc de jauger la difficulté des calculs et définissent les limites de la machine. A l’enseignant de déterminer le niveau de difficulté.
Première étape: découverte
Dans notre exemple nous allons utiliser la configuration 3, 2 Vous pouvez utiliser 3,1 pour limiter le produit à la première centaine.

Voilà ce qu’on obtient sur le site: la machine est dans son état initial, qui correspond à l’opération : 1×1=1 ou 1:1=1 :
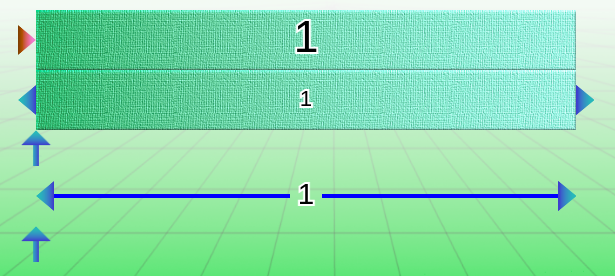
Dans le cadre d’une multiplication, la barre du haut est le produit, celle du milieu est le multiplicande et celle du bas le multiplicateur.
Pour une division, la barre du haut est le dividende, la barre du milieu est le quotient entier et celle du bas, le diviseur.
Bien sûr, ces termes techniques sont à destination de l’enseignant, pas des élèves, du moins dans un premier temps !
Il y a deux façons d’utiliser le schéma multiplicatif. C’est le rôle de la flèche rouge, nous reviendrons là-dessus plus tard. Pour modifier la valeur numérique dans une barre, il faut cliquer sur les flèches aux extrémités ou sur la flèche de déplacement, sous la barre. Voyons ce que cela pourrait donner :
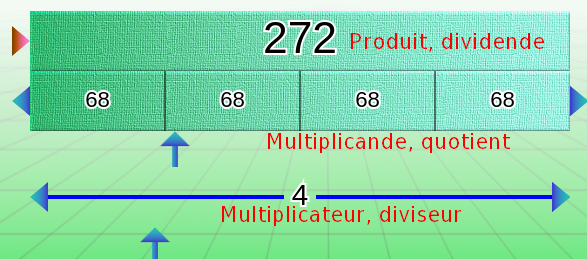
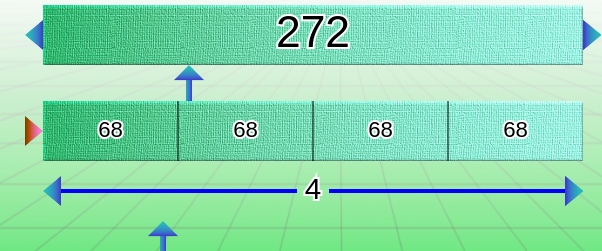
Nous avons donc l’opération :
272 = 68 x 4 ou 68 = 272 : 4 ou 4 = 272 : 68 (nous utilisons l’écriture « : » courante à l’école primaire pour signifier la division entière en ligne).
Problématiser sans attendre
Pour nommer les barres, les termes techniques sont compliqués et risquent de freiner l’acquisition de la compréhension du modèle. Mieux vaut utiliser une analogie; on peut partir d’un exemple de répartition d’objets en paquets d’unités – prendre des billes pour un cas concret :
La barre de produit ou du dividende pourrait devenir la barre des unités (nombre de billes).
Le multiplicande ou quotient devient la taille des paquets ou la taille des parts
Le multiplicateur ou diviseur devient le nombre de paquets ou le nombre de parts

À partir d’une situation numérique donnée, on peut demander aux élèves d’inventer des situations où l’on pourrait rencontrer ces nombres. On peut commencer, bien sûr, par les situations de multiplication et ne traiter qu’elles. Mais, grâce à ce modèle, on arrive assez rapidement à inventer des problèmes simples faisant appel à la multiplication ou à la division, à partir d’une seule représentation :
(a) J’ai 4 paquets de 68 billes. Combien ai-je de billes en tout ?
(b) Alice a 272 billes. Elle les répartit en 4 paquets égaux. Combien de billes y a-t-il dans un paquet ?
(c) Alice répartit ses 272 billes en paquets de 68 billes. Combien de paquets fait-elle ?
Dans le cas (a) la réponse se lit donc sur la barre « nombre d’unités ». La réponse du cas (b) se lit sur la barre « taille des paquets ». Enfin la réponse du cas (c) se lit sur la barre « nombre de paquets ».
Le point d’interrogation pour indiquer où se trouve la réponse
Servez-vous de l’étiquette « point d’interrogation » pour indiquer où se trouve la barre de la réponse. Lorsque vous placez l’étiquette sur une barre, l’affichage numérique disparaît. 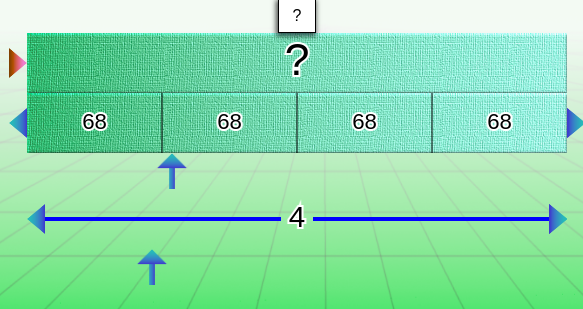
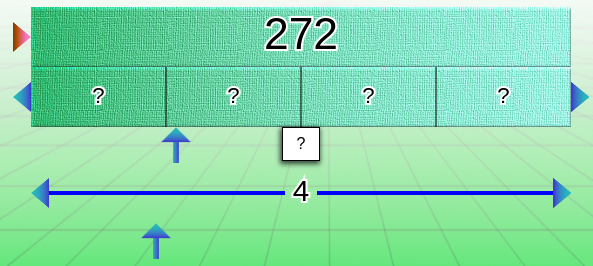
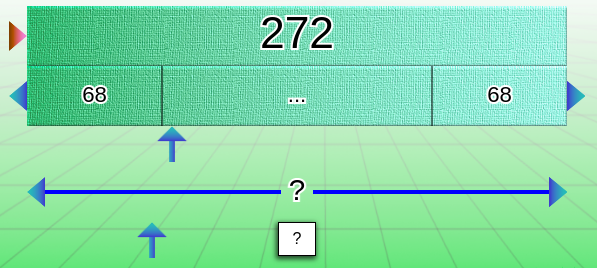
Dans le dernier cas, lorsqu’on place le point d’interrogation sur la barre du multiplicateur/diviseur, il y a une répercussion sur l’affichage de la barre du milieu, avec l’apparition de trois points « … » (lorsque c’est possible) pour éviter que les élèves se contentent de compter les cases !
L’utilisation du point d’interrogation permet, dans un premier temps, de vérifier que l’élève a bien compris le fonctionnement de la barre et qu’il va chercher la réponse au bon endroit.
Dans un second temps, en proposant des problèmes avec le point d’interrogation déjà positionné sur une barre, les élèves devront trouver les calculs à effectuer ainsi que la réponse, qui sera validée en retirant le point d’interrogation.
Des problèmes à foison
Un exercice très stimulant pour les élèves consiste à leur laisser la machine telle que nous l’avons paramétrée, de leur soumettre un problème, et de leur demander de le modéliser. Bien sûr, ils doivent aussi indiquer la barre sur laquelle on va lire la réponse, en positionnant le point d’interrogation.
Dans une séance il y a donc une phase de recherche individuelle (ou en petit groupe mais attention : il faut veiller à ce que chaque élève manipule) et une phase de restitution ou l’on discute des solutions proposées.
Il est conseillé de traiter plusieurs problèmes sur une séance; ne pas s’appesantir sur un seul énoncé. Bien entendu cette démarche a plus de sens si on alterne des problèmes nécessitant une multiplication et ceux avec divisions !
Attention toutefois à certains types d’énoncés. Ceux qui font intervenir des configurations rectangulaires (type calcul de la surface du rectangle) ou des produits cartésiens (nombre de combinaisons…) se prêtent assez mal à l’interprétation sémantique de nos barres (nombre de paquets et taille des paquets) puisque dans ce cas, les données sont interchangeables. On évitera donc ce type de problème dans la phase d’approche du modèle.
Attention aussi à la manipulation du modèle; comme vous le constatez, dans ce mode de fonctionnement, on ne peut pas saisir directement le produit/dividende. Il faut manipuler les deux autres barres, ce qui n’est pas toujours évident. Utilisez la gomme pour remettre le schéma dans un état initial.
Une variante pour la recherche de diviseurs et la décomposition
C’est l’avantage du numérique, on peut un peu améliorer les choses. On peut aussi les compliquer ! alors à vous de juger si la variante est intéressante pour vos élèves.
En cliquant sur la flèche rouge, on fait basculer le schéma dans un deuxième mode de fonctionnement, plus approprié lorsqu’on cherche un diviseur ou un quotient à partir du dividende.
D’abord, avec la flèche du haut, on indique le dividende. En actionnant ensuite la flèche du bas, on peut calculer automatiquement les diviseurs et les quotients (entiers évidemment).
On arrive à des décompositions du genre :
272
= 1 x 272 = 2 x 136 = 4 x 68 = 8 x 34 = 16 x 17
= 17 x 16 = 34 x 8 = 68 x 4 = 136 x 2 = 272 x 1
Le tout sans effort. Ceci nous permet d’explorer les propriétés des nombres entiers, de mettre en évidence la commutativité de la multiplication puisque nous observons une symétrie dans les écritures.
Des élèves vraiment à l’aise avec le modèle devraient avoir le choix du mode de fonctionnement.
L’entraînement sur le site
Actilud.com, numération et problèmes de base, H2: multiplication, division avec schéma
Dans la fenêtre de dialogue des paramètres vous pouvez très finement régler la difficulté et la nature du travail à faire.
Soucis de compréhension ?
Si vos élèves ont des problèmes de compréhension, ce qui est très fréquent, vous pouvez polariser le travail sur un seul type d’énoncé. Par exemple, choisir « billes » dans l’entrée « énoncé ». Pour ce type d’énoncé, vous avez la possibilité de sélectionner la multiplication, la division quotition ou la division partition. Lorsque les élèves arrivent à résoudre les trois types d’opération, vous pouvez demander au programme d’effectuer un choix aléatoire, toujours avec le même problème. Evidemment, les données changent aléatoirement.
Une fois ce problème maîtrisé, on peut passer à un suivant.
Dans l’entrée « énoncés » vous remarquez que les problèmes sont suivis par une lettre, qui correspond au type d’énoncé :
a: problème de multiplication ou division simples
b: configuration rectangulaire (quand il y a une longueur et une largeur)
c: n fois plus ou moins
d: produit cartésien
Cette distinction permet de limiter les choix aléatoires à certaines catégories afin d’améliorer la progressivité des apprentissages.
Pendant la période d’entraînement vous avez donc la possibilité d’adapter très finement l’apprentissage à chaque groupe d’élèves. Comme les entrées des paramètres sont toujours numérotées, il est facile d’indiquer, au tableau, la série à faire par leurs numéros, comme nous l’avons fait nous-même dans cet article :

Ici la consigne est : H2, 4-3-2-7. Les élèves de ce groupe ne travailleront que sur les énoncés « chocolat », devront trouver et effectuer les calculs, avec des produits ou des dividendes allant jusqu’à 1000. Il s’agit d’une phase de consolidation puisque le type de problème sera choisi aléatoirement.
N’hésitez pas à modifier les pistes que nous dégageons ici. Le site Actilud n’est pas normatif, les exercices proposés s’adaptent à votre façon de travailler et à votre classe. Profitez du site pour alterner les phases manipulatoires de recherche avec des restitutions collectives.
Pour en savoir plus voici la vidéo. Si elle ne s’affiche pas, actualisez la page.
