par Le schéma cartésien est une alternative au schéma multiplicatif de base. Il est beaucoup plus simple à comprendre que son analogue, mais il est aussi plus limité.
Présentation
Le principe du schéma cartésien repose sur le calcul de l’aire du rectangle :
A = L x l
L’aire est égale à la longueur multipliée par la largeur
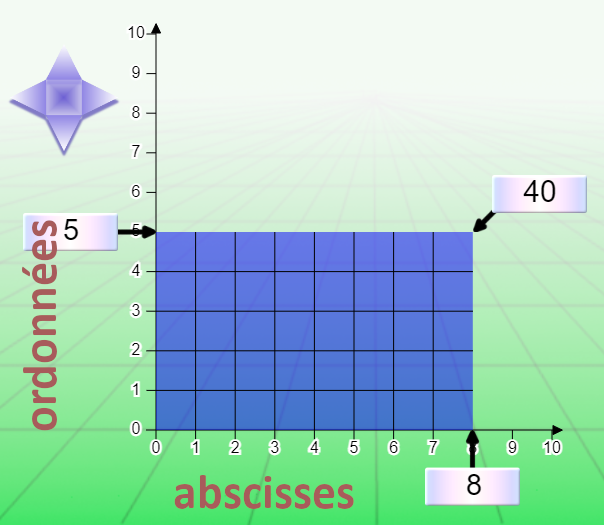On peut agir sur l’axe des abscisses, sur l’axe des ordonnées, sur l’aire, en déplaçant les contrôleurs correspondants. Lorsque les nombres sont grands, on peut affiner la position à l’unité à l’aide du contrôleur en forme d’étoile à 4 flèches.
Limites
Contrairement au diagramme cartésien “mathématique”, dont les axes ont une longueur infinie, le modèle cartésien, dont les axes sont finis, est plus limité. Avec lui, il n’est pas possible de retrouver tous les diviseurs d’un nombre.
Prenons le schéma ci-dessus. Nous voyons que les axes sont gradués de 0 à 10. Il n’est donc pas possible, sur ce modèle, d’utiliser des valeurs plus grandes. Le problème suivant ne peut donc pas être résolu à l’aide de ce schéma cartésien :
Les 60 sièges d’une salle de spectacle sont répartis en 4 rangées identiques. Combien y a-t-il de sièges dans une rangée ?
La réponse, 15, n’entre pas sur les axes. Pour résoudre le problème, il faut modifier l’échelle du modèle et choisir, par exemple, des axes limités à 32. Mais, si la résolution du problème ci-dessus devient possible, la limite est toujours présente pour les valeurs supérieures à 32. Ainsi, par exemple, modéliser une opération aussi simple que 100 x 1 n’est pas possible sur le modèle 32×32.
Cependant, tous les problèmes proposés sur Actilud peuvent être résolus avec les deux schémas. C’est pour cette raison que, dans le paramétrage, la valeur maximale des opérandes est indiquée.
Mais, lorsque vous faites une présentation libre du schéma cartésien, tenez compte de cette limite lorsque vous créez vos propres problèmes.
Intérêt
Les problèmes de répartition rectangulaire et les problèmes combinatoires sont bien mieux traités par ce modèle que par son analogue, le modèle multiplicatif en barres.
Le modèle multiplicatif en barre organise les données en “parts” et en “taille de parts”.
Calculs combinatoires
Dans les calculs combinatoires en particulier, ce découpage n’a aucun sens. Dans le problème :
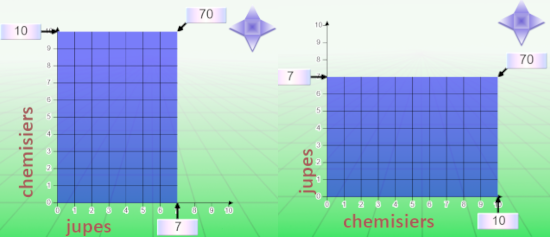
Combien d’assortiments peut-on faire avec 10 chemisiers et 7 jupes ?
le découpage en parts et en tailles de parts est artificiel. Dans le modèle cartésien, il n’existe pas. On peut utiliser indifféremment l’axe des abscisses ou des ordonnées pour les jupes et les chemisiers, ce qui donne deux schémas possibles :
Configuration rectangulaire
Dans la configuration rectangulaire, l’organisation en parts et en nombre de parts est possible :
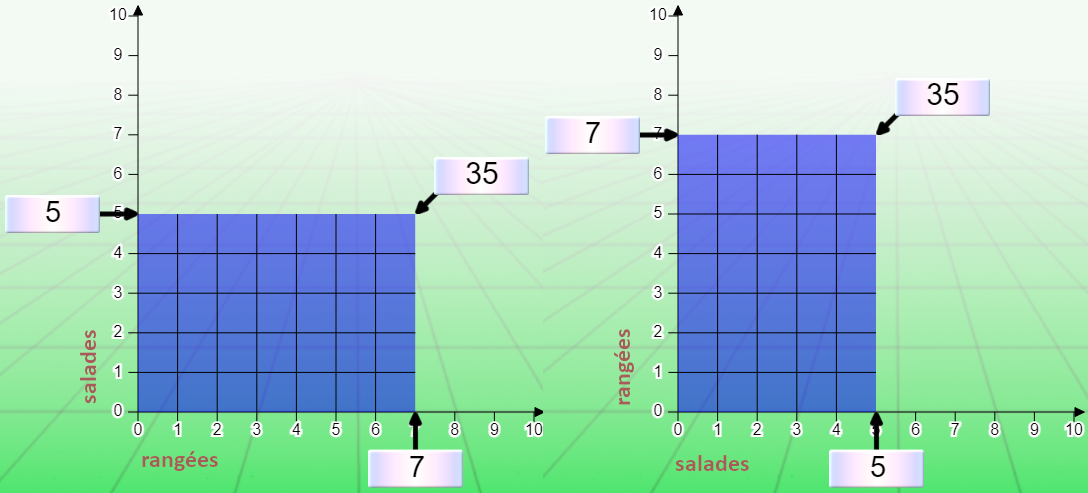
Un jardiner plante 7 rangées de 5 salades. Combien de salades a-t-il plantées en tout ?
Dans le modèle classique, si on respecte l’énoncé à la lettre, une seule configuration est possible:
La rangée est assimilée à une part. Le nombre de salades dans la rangée est la taille des parts.
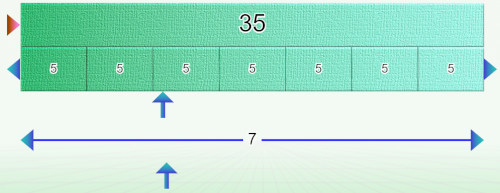
Dans le paramétrage des problèmes, si vous choisissez l’option “placer les étiquettes sur le schéma”, cette répartition sera la seule acceptée.
Le schéma cartésien, quant à lui, accepte les deux configurations :
N fois plus, N fois moins
Ce type de problème se traite exactement comme la configuration rectangulaire.
Soit le problème suivant :
Bob économise 2€. Alice en économise 6 fois plus. Combien économise-t-elle ?
Comme pour la configuration rectangulaire, le schéma multiplicatif en barres n’accepte qu’une seule configuration: la valeur n fois plus/moins doit figurer en tant que nombre de parts, soit 6, et la valeur 2 € est la taille des parts.
Sur le schéma cartésien, la position des nombres sur l’axe des abscisses ou des ordonnées n’a pas d’importance. Il y a donc deux représentations possibles.
Initiation au modèle
Compter les cases dans un premier temps
C’est là tout l’intérêt de ce modèle. Au départ, on compte le nombre de cases pour arriver à la conclusion que le nombre de cases est donné par la multiplication des valeurs des abscisses et des ordonnées.
Ainsi, dans un premier temps, on travaille sur le modèle le plus simple, avec des axes limités à 10. L’aire est alors découpée en carreaux de taille 1×1, donc des carreaux-unités. Le problème des salades et des rangées devient alors très facile à comprendre, si on assimile chaque carreau à une salade. Les problèmes combinatoires sont facilités, puisque chaque carreau correspond à une combinaison.
Bien sûr, le modèle est aussi une bonne préparation au calcul de l’aire du rectangle. De fait, il sera très facile d’amener la formule longueur x largeur si les élèves ont déjà, dans leur scolarité, rencontré cette situation.
Attention, le comptage ne doit pas être pérennisé. Il faut très vite amener les élèves à calculer l’aire, car sinon le passage d’échelle sera difficile.
Passage d’échelle
Dans les axes de taille supérieure, les carreaux sont formés de 10 x 10 unités. Chaque carreau représente donc 100 unités. Il faudra attirer l’attention des élèves sur ce changement d’échelle en traitant d’abord l’aire 10×10 dans un problème sur un diagramme cartésien limité à 10, puis en reprenant le même problème sur un diagramme plus grand (100 par 100 est idéal) où un carreau correspond aux 10 x 10 carreaux du précédent diagramme. Si, à ce stade, les élèves comptent toujours le nombre de carreaux, il faudra multiplier la réponse par 100.
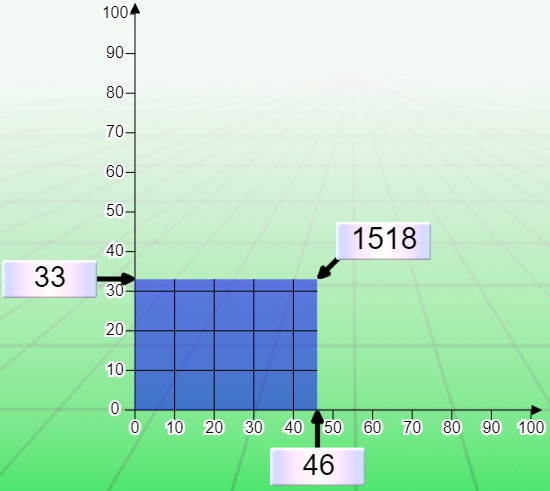
Notez cependant que certains carreaux risquent bien d’être incomplets, comme dans l’illustration ci-dessous :
Passage d’un schéma à l’autre
Dans les problèmes H3, on peut basculer facilement d’un schéma à l’autre en cliquant sur cette icône.
Conclusion : de la souplesse
Permettre aux élèves de choisir le schéma le plus approprié pour résoudre un problème développe une certaine souplesse intellectuelle et limite la dépendance à un modèle donné. De plus, cette nouvelle approche permet de débloquer des élèves qui ont du mal à comprendre l’autre modèle.
Même si au départ, cela peut être contraignant, varier les représentations est une ouverture : on montre qu’une même situation peut être modélisée de plusieurs manières. C’est un pas vers plus d’agilité mentale. N’oubliez pas aussi, que si les élèves devraient être capables d’utiliser les deux représentations, ils ont aussi le droit d’avoir des préférences quand au choix du modèle. Sachant que notre objectif final est bien de se passer complètement des modèles, grâce à un entraînement systématique et bien organisé.