Crée un écart entre deux items a et b utilisant une série ordonnée régulière.

Pour l’utiliser il faut donc au moins une série ordonnée régulière.

Pour faciliter la résolution, les booléens sont conseillés. C’est l’une des instructions les plus complexes des intégrammes.

Série ordonnée: série contenant des valeurs qui sont toutes croissantes ou toutes décroissantes.
Série ordonnée régulière: série croissante ou décroissante dont les valeurs sont séparées par le même intervalle.

Énigme du char à voile

Il y a trois ans d’écart entre Lucas et l’ado qui pilote le char vert.
Il y a 20 minutes d’écart entre la personne qui pilote le char bleu et celle de 17 ans.

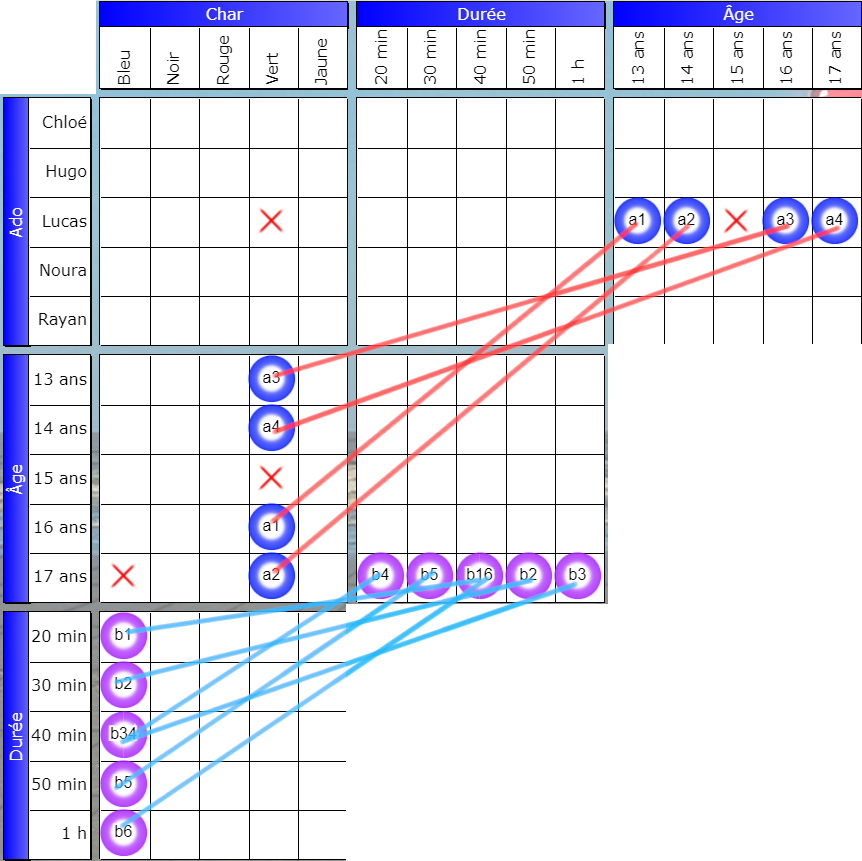
Les traits rouges et bleus représentent les relations entre les cases par-delà les grilles, matérialisées par les booléens.

Trait rouge

Si Lucas a 13 ans, le pilote du char vert en a 16, et inversement.
Si Lucas a 14 ans, le pilote du char vert en a 17, et inversement.
Si Lucas a 16 ans, le pilote du char vert en a 13, et inversement.
Si Lucas a 17 ans, le pilote du char vert en a 14, et inversement.
Où l’on constate que ni Lucas ni le pilote du char vert ne peuvent avoir 15 ans, car 15-3=12, ce qui est hors limite, et 15+3=18, ce qui est aussi hors limite.

Trait bleu

Là l’utilisation des booléens “union” est indispensable :

Si le pilote du char bleu roule pendant 20mn ou pendant 1h, l’ado de 17 ans roule pendant 40mn, et inversement.
Si l’ado de 17 ans roule pendant 20mn ou pendant 1h, le pilote du char bleu roule pendant 40mn, et inversement.

Le reste est plus facile :

Si le pilote du char bleu roule pendant 30mn, l’ado de 17 ans roule pendant 50mn, et inversement.
Si le pilote du char bleu roule pendant 50mn, l’ado de 17 ans roule pendant 30mn, et inversement.

Les signes faux

Ceux qui sont présents dans les rangées de booléens indiquent des positions qui sont hors de la limite.
On découvre aussi des signes faux à l’intersection des rangées : Lucas ne peut pas piloter le char vert, et l’ado de 17 ans ne pilote pas le char bleu.

Création de booléens union sur le site

C’est le moment d’utiliser le collecteur de booléens. Y placer un premier booléen puis un second, différent. Il en sortira un booléen union.

Concepteur

Choisit aléatoirement une série ordonnée régulière D, deux items a et b qui s’y réfèrent, et un écart |i| entre les deux items. Cet écart est une valeur absolue : il va dans les deux sens (+i, -i).

Le saut est la distance qui doit être indiquée en nombre de cases qui séparent deux items de chaque rangée. Le saut sera converti en unités spécifiques à la série (années, minutes, etc.) lors de la génération des propositions formelles. La valeur de 0 donne un choix aléatoire. Si n est le nombre de cases par rangée, pour qu’un saut soit calculable, le minimum doit être ⌊n/2⌋ et le maximum n-2. Soit une valeur entre 2 et 3 pour une rangée de 5 cases.

⌊n/2⌋ signifie: partie entière de n/2

Isolé: si l’instruction fonctionne en mode isolé, le concepteur ne choisit pas les rangées qui contiennent déjà des signes, y compris des booléens.

Nombre maximum d’exécutions de cette instruction.

Proposition formelle générée

D : Δ(a,b) = ± i
l’écart dans D entre a et b est de i
Âge : Δ (Lucas, Vert) = ± 3
Durée : Δ (Bleu, 17 ans) = ± 20

D: en-tête de la série partagée contenant une relation d’ordre régulière.
a,b,: items utilisant D
± i, : valeur des intervalles, en unités de D; i est appliqué en positif et en négatif car c’est un écart.