Comment utiliser les dominos décimaux pour  l’apprentissage de la dizaine et le comptage jusqu’à 100.

Ça y est, les élèves comptent jusqu’à 10. Ils ont l’habitude d’utiliser le domino-unité à numération décimale pour ajouter ou retirer des jetons un à un. Ils sont capables de compter à partir de la pile de 5. Ils arrivent même à créer des nombres en ôtant quelques jetons, comme obtenir un 9 à partir de la pile de 10.

Il faut maintenant aller plus loin et comprendre la dizaine. Pour cela, le domino décimal est une aide intéressante.

Dominos “dizaines” et “unités”

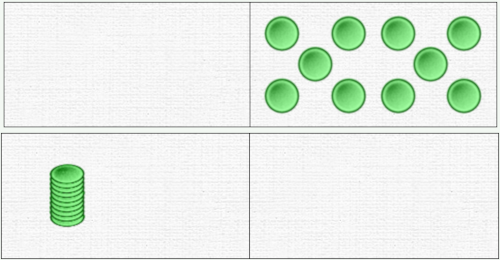
En travail libre, nous utilisons pour commencer une barre contenant deux dominos, “dizaines” et “unités”. Paramétrage 1,2,1,-.

À gauche, nous avons le sélecteur avec le jeton-unité, la pile de 10 et la pile de 5.

Nous utilisons à nouveau un tableau numérique interactif : comme toujours, le geste est important, il doit être vu, d’où l’importance de théâtraliser l’activité.

Découvrir, passer, approfondir la notion de dizaine

Le mieux est de bien expliquer à l’avance aux élèves ce que nous allons faire; dans des situations nouvelles, il est important d’être explicite et de les préparer à la nouveauté. Aussi, montrons-leur la planche de travail ci-dessus et indiquons-leur notre objectif: placer 11 jetons. Demandons-leur ce qu’il se passe si on ajoute un jeton lorsqu’il y en a déjà 10, pour en obtenir 11, et laissons-les un peu s’exprimer. Les élèves seront sans doute étonnés de trouver deux dominos côte à côte – leur expliquer que nous allons nous servir des deux dominos. Il y a fort à parier qu’ils proposent de placer l’unité supplémentaire dans le deuxième domino. Ce qui, vu l’information dont ils disposent, est une idée qui mérite d’être testée !

Démarrons l’activité. Créons la dizaine par itération de l’unité en utilisant le domino de droite :

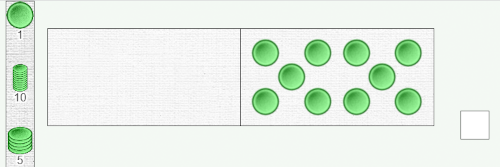
Pour arriver à 11, les élèves vont peut-être proposer l’ajout du jeton supplémentaire dans l’autre domino. Mais avant cela, il vaut mieux vérifier qu’il n’est effectivement pas possible de l’ajouter à nos dix premiers jetons. Donc, tentons de le faire : ajoutons un jeton à la dizaine déjà présente et voyons le résultat.

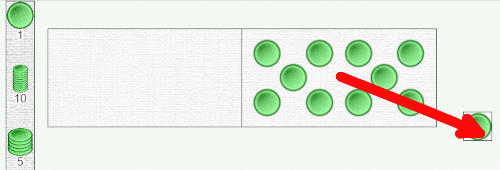
Impossible de placer un jeton supplémentaire dans le domino : un son d’erreur retentit, le jeton rejoint la petite case, notre salle d’attente. Il n’y a manifestement plus de place dans le domino de droite pour un jeton de plus.

Essayons alors de déplacer le jeton dans le domino de gauche…

C’est à nouveau un refus catégorique. On déplace le jeton sur le domino de gauche, mais celui-ci retourne à sa place initiale.

L’enseignant en profite pour donner une information importante : le domino de gauche n’accepte que les piles de 10 jetons ! Voilà pourquoi  le jeton tout seul est refusé.

Deuxième information importante : on peut construire une pile à partir de 10 jetons. Comment faire ? L’enseignant saisit alors un jeton parmi les dix dans le domino de droite, et le déplace dans le domino de gauche. Tous les jetons du domino de droite se rassemblent alors et s’empilent : nous obtenons une pile à gauche, et rien à droite.

L’animation qui se produit à ce moment est très importante pour la compréhension : les jetons se déplacent et s’empilent. La pile n’est donc pas un objet à part : il s’agit bien des jetons, mais rangés différemment. Ne pas hésiter à répéter l’animation. On replace la pile de 10 dans le domino de droite : la pile se défait et les dix jetons se rangent. On recommence pour bien montrer comment la pile se forme. Il existe une activité similaire que l’on peut faire sans l’informatique, avec les barres de cubes.

VIdéo: le passage à la dizaine.

La formation de la pile ne fonctionne qu’avec 10 jetons. S’il en manque un, le jeton est simplement refusé par le domino de gauche, et il rejoint la case d’attente. On peut le montrer maintenant aux élèves ou les laisser expérimenter plus tard pour le découvrir eux-mêmes.

Revenons à notre objectif initial : comment placer 11 jetons. La solution apparaît alors assez facilement. Nous en avons dix dans la pile, et le domino de droite est vide. Il suffit donc d’y ajouter un jeton : nous en avons bien 11 : 10 à gauche, 1 à droite.

Pour introduire le concept de dizaine, il faut encore assimiler la pile de 10 jetons à la dizaine, ce qui ne devrait pas être trop difficile: comme il y a dix jetons dans une pile, c’est une dizaine, car on entend “dix” dans “dizaine”. On généralisera ce concept avec d’autres collections d’objets.

Arrivés à ce point, les élèves pourraient être curieux et impatients d’utiliser les dominos : on peut les laisser explorer. Cette phase est importante : il faudrait que chaque élève puisse prendre son temps à effectuer la manipulation pour bien la comprendre et l’assimiler. Pour cela, les tablettes ou ordinateurs individuels sont de bons alliés.

Aller plus loin

Les nombres jusqu’à 19

On peut construire chacun de ces nombres à l’aide de nos dominos, au moment où on les étudie. On peut certes déposer les jetons un à un à partir du domino vide, mais l’idéal est évidemment de surcompter à partir de 10. Pour bien marquer le passage à la dizaine, je suggère de déposer la barre de 10 d’abord dans le domino-unités, ce qui produit 10 jetons et rend obligatoire le passage à la dizaine, contribuant ainsi au renforcement de la notion.

L’apprentissage par cœur de la dénomination est important : jusqu’à 16 il faut apprendre la prononciation du nombre. La régularité s’installe à partir de 17 et  peut être illustrée par le domino (une dizaine et 7 unités, dix et sept, dix-sept).

Le nombre 20

… se manipule comme le nombre 10 : sur nos deux dominos, 20 est représenté au départ par une dizaine et 10 unités et nous effectuons le passage.

Les nombres jusqu’à 99

… suivent la même routine.

La section suivante ne concerne que les élèves Français. Les autres ont la chance d’avoir “septante”, “octante” et “nonante” !

Cas de 70

Le “soixante-dix” peut facilement l’illustrer avec les dominos décimaux, en plaçant 6 dizaines et dix unités, et en effectuant le passage: on a bien soixante et dix unités qui s’écrit 70.

Cas de 80

Là c’est un peu plus compliqué pour les Français. Pour dire “quatre-vingts”, nous n’avons pas de piles de 20, il va donc falloir montrer cela avec des piles de 10. Comme il n’est pas possible de prendre deux piles en même temps, on fera une pause toutes les deux piles pour expliquer qu’il y en a 20, puis deux fois 20, trois fois 20 et finalement quatre fois 20.

Cas de 90

C’est le pompon ! Pour “quatre-vingt-dix” on va donc fonctionner comme 80, mais en ajoutant encore une pile de 10 après quatre-vingts.

Le nombre 100

Avec deux dominos, le nombre 100 s’affiche sous deux formes : 100 = 9 dizaines et 10 unités, que l’on passe à 10 dizaines.

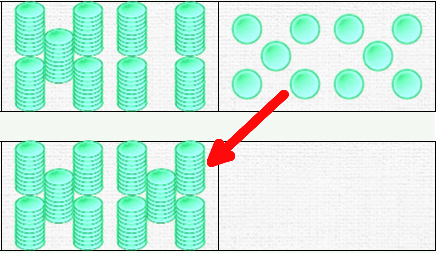
On remarque que l’on pourrait continuer et ajouter des unités – jusqu’à une valeur de 110. Mais il vaut mieux s’arrêter là. C’est le moment de faire apparaître une troisième forme de domino : le domino-centaines ! Pour cela, on passe à trois dominos, en paramétrant centaines, dizaines et unités... et on reproduit le passage. Je propose de désigner l’amoncellement de piles de 10 formant la centaine par le terme de “tas” ou “tas de piles”, pour le différencier de “pile”.

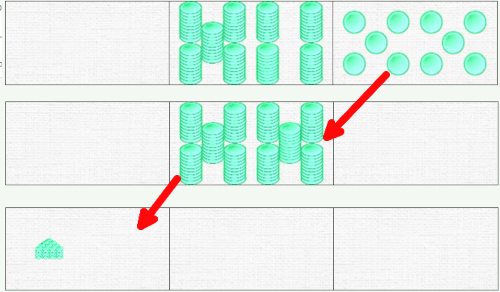
Avec trois dominos nous avons donc trois représentations possibles du nombre 100. La troisième forme étant celle qu’il faut retenir pour écrire le nombre. Cf le point de vigilance ci-dessous, qui est valable pour 10 dizaines comme pour 10 unités.

Une fois arrivé dans le domino-centaines, le tas de 100 diminue un peu de taille; lorsqu’il y en a plusieurs, cela facilite le comptage.

Au-delà de 100…

Toujours la même routine, on s’arrête à 1000 car là, il n’y a plus de dominos !

L’écriture du nombre

Un point de vigilance

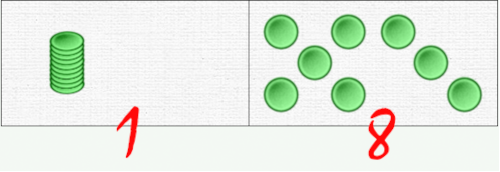
Dans le système décimal il y a dix chiffres, de 0 à 9. Il n’y a qu’une seule façon de représenter la dizaine par un nombre: c’est 10 – soit une dizaine, 0 unité.

Mais, dans nos dominos à numération décimale, il y a deux représentations :

Il ne faut donc surtout pas passer trop vite à l’écriture décimale, comme on pourrait être tenté de le faire sans réfléchir !

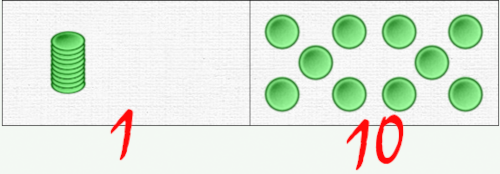
Comme souvent, la facilité est un piège !

Pour la petite histoire, lors de la mise au point j’avais automatisé le passage de la dizaine. Dès que le domino-unités recevait le dixième jeton, les dix jetons se regroupaient et rejoignaient le domino-dizaines. Finalement, j’ai abandonné l’idée car elle ne permet pas de bien comprendre qu’une dizaine = 10 unités: on n’a pas le temps de voir les dix jetons car ils sont immédiatement transformés en une dizaine. Il m’a semblé bien plus pertinent de rendre obligatoire une manipulation spécifique, volontaire, de la part de l’élève.

De plus, mathématiquement la formulation suivante est exacte : 20  = 1 dizaine + 10 unités. Il faudrait que nos élèves en aient conscience, et pour cela, on peut compter les jetons.

Bien entendu, cette remarque est valable aussi dans le cas du nombre 100, avec 10 dizaines.

Le statut particulier du domino 10

Nonobstant le point de vigilance décrit ci-dessus, l’écriture du nombre découle naturellement de la disposition des dizaines et des unités dans le domino. Mais une petite explication complémentaire peut être intéressante pour expliquer que 1 dizaine et dix unités, c’est 20 et non 110.

Dans le système décimal il y a dix signes pour désigner les chiffres: 0 à 9. On peut associer les premières configurations de nos domino-unités à un chiffre (et on parle bien de “chiffre”, le signe, pas de nombre).

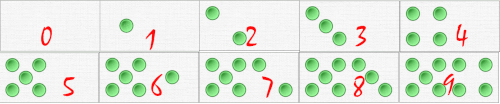
On peut placarder en classe une bande numérique de ce genre.

On constate ici que l’on ne fait qu’associer la représentation conventionnelle du domino avec une autre représentation conventionnelle, le chiffre. Les élèves devraient être habitués à cette représentation des dominos. Il y a un chiffre différent, et un seul, pour désigner chacun de ces dominos.

Que se passe-t-il pour le domino 10 ?

 

On n’a plus de chiffre pour désigner ce domino. Le stock est épuisé ! La seule possibilité de le représenter est le nombre 10. Mais ce nombre est formé de deux chiffres, 1 et 0. Comment faire ? C’est là qu’intervient le passage avec nos deux dominos.

Écrire des “grands” nombres sans même savoir les nommer

Pourquoi pas ?

Une fois que les élèves savent manipuler les dominos et écrire les chiffres de 0 à 9, on peut très bien leur proposer l’activité suivante : utiliser les dominos pour écrire des nombres (inférieurs à 100 tout de même) sans même les avoir étudiés. À l’enseignant de nommer le nombre.

Voici deux cas; le deuxième exige une manipulation intermédiaire.

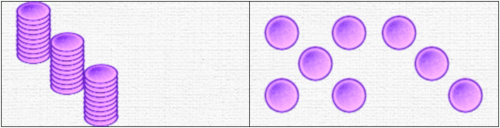
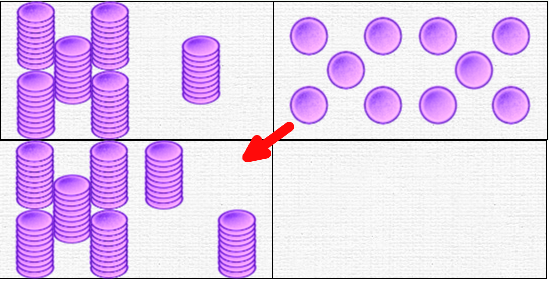
Tableaux numériques

À ce stade on peut utiliser le tableau pour écrire le nombre de dizaines et d’unités. Le tableau permet aux élèves de comprendre la logique qui sous-tend l’écriture des nombres décimaux et les rend capable d’écrire quelques égalités simples. On peut abréger “dizaines” et “unités” en “d” et “u”. On remarquera que les cases “c”,”d”,”u” ne désignent pas le chiffre des centaines, dizaines et unités, mais  le nombre de centaines, dizaines, unités. Ce point est fondamental. S’il n’est pas compris, on va au-devant de nombreuses erreurs et il est impossible de comprendre des nombres décrits comme “5 dizaines et 18 unités”.

70 :

d	u
6	10
7	0

Comme on le voit, on écrit 10 unités dans la colonne “u” si le domino le présente, mais on ajoute une seconde ligne pour la conversion. On prépare ainsi les élèves à des équivalences plus complexes, que nous pourrons aborder lorsque 100 sera dépassé : par exemple 15 dizaines = 1 centaine et 5 dizaines. Cela les prépare aussi au transfert de la retenue dans les additions.

Quand on arrive à 100, on utilisera le tableau à trois colonnes, avec les centaines “c”. C’est exactement le même principe. La représentation à trois étages de 100 vue plus haut peut donc s’écrire ainsi :

100 :

c	d	u
0	9	10
0	10	0
1	0	0

Conversions entre unités, dizaines, centaines

Pour étudier les conversions on peut transposer dans les dominos des énoncés faisant intervenir la décomposition d’un nombre. Voici un cas déjà complexe; il est recommandé de commencer par un exemple plus simple.

Écrire le nombre correspondant à :

c	d	u
4	16	14

L’élève peut se débrouiller assez facilement avec les dominos.

Le moyen le plus immédiat est d’utiliser une barre de 3 dominos et de poser un à un chaque élément, en regroupant les tas de 10 vers la puissance de 10 supérieure. Ceci demande un comptage rigoureux mais la méthode est simple à mettre en œuvre.

Une autre méthode utilise deux barres de dominos mais elle ne fonctionne qu’avec certains énoncés : il ne faut pas dépasser 20 dizaines et 20 unités, ce qui est le cas ici. Elle permet de mieux vérifier le nombre de pions posés.

L’élève commence par poser tous les pions, en comptant les éléments dans le domino du haut et du bas correspondant.

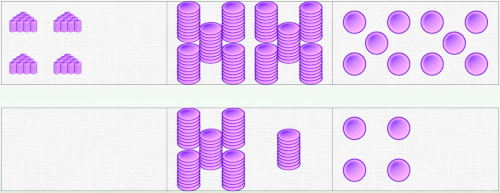
Son objectif est de regrouper tous les pions dans une seule barre. Il n’est pas obligé de respecter un ordre particulier, mais il doit tenir compte des contraintes de taille – 10 éléments maximum par domino, ce qui impose tout de même de séquencer correctement ses actions. Il faudra qu’il regroupe les dix dizaines de la barre du haut vers une centaine, et les dix unités vers une dizaine. Il faut aussi ajouter les autres pions et vérifier qu’il n’y a plus de dominos avec 10 éléments (on évitera d’arriver à 10 centaines).

Au final, il obtient ceci, qui est la réponse. Il n’y a plus qu’à l’écrire en chiffres : 574

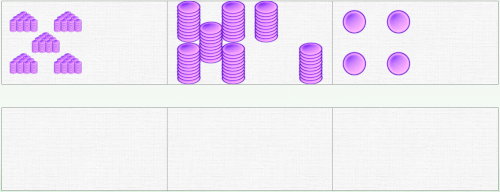
Bien sûr, on peu démarrer les conversions avec seulement des dizaines et des unités.

La règle
Pour écrire un nombre à partir des dominos décimaux, on doit d’abord effectuer tous les passages.

Ce n’est qu’ensuite que l’on peut compter le nombre de centaines, de dizaines et d’unités.

Autres activités sur le site

Les réglettes Cuisenaire
Pour le dénombrement et la décomposition des nombres.

Le schéma en barres avec des cases
Pour la décomposition des nombres.

La pesée virtuelle
Avec des fruits légers, dans le mode “comparer avec des masses virtuelles”, pour compter le nombre de triangles.

La numération avec des billes
En travail libre, poser des billes de différentes couleurs sur les lignes, compter des billes ou des collections de mêmes couleurs.

 

 

Lien vers l’activité.