Dans la section Numération et opérations, vous trouverez un assortiment de bouliers disponibles en travail libre, pour une utilisation collective, ou en exercices individuels.

Le boulier de comptage

Le boulier de comptage sur Actilud reprend les codes du boulier enfantin traditionnel. Il est formé de 10 lignes de dix jetons, chaque jeton valant une unité. Il n’y a pas de logique positionnelle : la valeur du jeton ne varie pas selon sa rangée.

Sur Actilud, les lignes ont des couleurs variées – ce qui plaît généralement aux enfants – mais chaque ligne est divisée en deux parties de 5 jetons, que l’on distingue très bien car elles utilisent des couleurs complémentaires. On facilite ainsi le sur-comptage à partir de 5.

Chaque boulier génère ses propres couleurs, qui ne sont jamais les mêmes d’une instance à l’autre.

Le boulier de comptage s’utilise en glissant un ou plusieurs jetons d’un côté à l’autre. Le sens du déplacement dépend du choix du modèle. Dans le menu de paramétrage, on peut en effet choisir un sens de déplacement de gauche vers la droite, ou l’inverse. Le sens qui semble le plus recommandé est le déplacement des jetons de la gauche vers la droite, car c’est le sens commun de l’écriture dans nos sociétés. Toutefois, Actilud fournit aussi le sens de droite vers gauche.

Comme son nom l’indique, le boulier de comptage est utile pour les élèves qui ont encore besoin de compter pour réussir un calcul.

L’intérêt est que l’on peut écrire les dizaines facilement, en déplaçant d’un seul geste une rangée de 10 jetons. Pour un déplacement de gauche à droite, on actionne le jeton le plus à gauche et on le déplace vers la droite, ce qui va pousser les autres.

La compréhension de la décomposition décimale est donc grandement facilitée : si je dois écrire 38, je glisse trois dizaines puis encore une ligne de 8 boules, effectuant ainsi la décomposition en dizaines : 38 = 10 + 10 + 10 + 8. Le nombre 8 peut lui-même se décomposer en prenant 5 jetons de la même couleur sur une ligne et en y ajoutant les 3 manquants. L’élève est ainsi invité de passer à une logique de comptage des unités à une logique de regroupement par dizaines et de sur-comptage.

Ce boulier convient pour des opérations sur des nombres entiers inférieurs ou égaux à 100, dont la somme ne dépasse pas 100.

En travail libre, l’utilisation du bloc-notes permet de visualiser les nombres tout au long des manipulations. Le logiciel additionne tous les jetons qui sont à droite (ou à gauche selon le modèle choisi), peu importe la répartition des jetons sur le boulier.

Le Suanpan, ou boulier chinois

Le Suanpan est un boulier à logique positionnelle. Les colonnes sont organisées de droite à gauche, du poids le plus faible à droite vers le plus fort à gauche, exactement comme sont représentés les nombres.

Les unités sont donc à droite, suivies par les dizaines dans la colonne immédiatement à gauche, puis il y a les centaines et ainsi de suite.

Chaque colonne est organisée en référence à l’anatomie de la main. Les deux jetons du haut, quinaires, correspondent aux deux mains. Les jetons du bas, unaires, correspondent aux 5 doigts de la main.

La valeur des jetons est multipliée par un facteur de 10 en passant d’une colonne à l’autre.

Pour écrire un nombre, on rapproche les jetons de la barre horizontale qui traverse le boulier. On descend donc les jetons quinaires et on monte les jetons unaires.

Voici une façon d’écrire le nombre 15 375  :

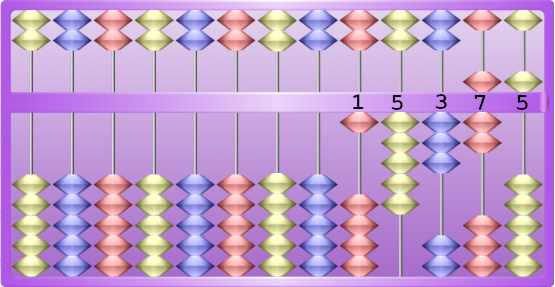
Notez que dans le nombre illustré ci-dessus il y a deux façons d’écrire le chiffre 5: soit avec 5 jetons dans la colonne du bas, soit avec un jeton quinaire dans la colonne du haut. La préférence doit aller vers l’écriture la plus compacte possible, à savoir un jeton quinaire plutôt que 5 jetons unaires.

Il y a trois façons d’écrire la dizaine; là encore, la plus compacte est à privilégier.

• un jeton quinaire et 5 jetons unités
• deux jetons quinaires
• un jeton unaire dans la dizaine supérieure, qui est la solution à retenir

Toute l’astuce consiste donc à transformer les jetons unaires, soit en quinaires, soit en jetons unaires de poids supérieur. Pour transformer 5 jetons unaire en un jeton quinaire,  un manipulateur aguerri fera un seul  geste avec le pouce et l’index, pour descendre un jeton quinaire et, en même temps, abaisser les 5 jetons unaires. Sur Actilud, comme le « toucher multiple » n’est pas programmé, il faut procéder en deux étapes.

La règle est donc simple :

• 5 jetons unaires se transforment en un jeton quinaire
• deux jetons quinaires, ou dix jetons unaires, se transforment en un jeton unaire de la dizaine supérieure (colonne à gauche)

On arrive ainsi, par réductions successives des jetons, à effectuer des calculs complexes. Sur Actilud, on proposera l’addition et la soustraction. Mais on peut aussi s’essayer aux multiplications ou aux divisions, en travail libre.

Le séparateur décimal

C’est une exclusivité pédagogique disponible uniquement sur Actilud ! Le séparateur décimal, la virgule pour les Français, est la petite languette, initialement à droite sur la barre, que l’on peut déplacer le long l’axe; elle indique le départ de la partie décimale. Essayez-la en travail libre avec le bloc-notes. Ceci permet d’utiliser le boulier avec des nombres décimaux.

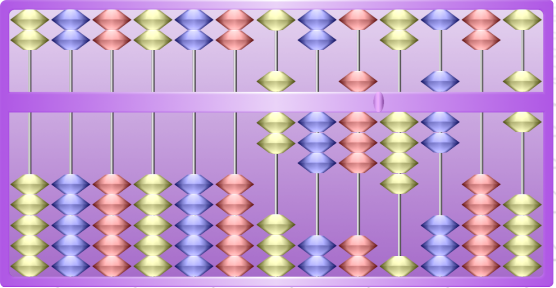
Sur Actilud, le Suanpan est disponible en 4 tailles différentes : 13, 10, 7 et 4 colonnes. Comme nous regroupons les nombres par paquets de trois chiffres, les colonnes sont colorées en trois couleurs, jaune, rouge et bleu. La couleur à gauche de la languette définit les unités (jaune par défaut si la languette est à droite), puis les dizaines (rouge), puis les centaines (bleu). Ensuite, on recommence avec la même couleur pour les unités de mille, les dizaines de mille, les centaines de mille, et ainsi de suite. Dans l’illustration ci-dessus, les unités sont en rouge car la languette a été déplacée.

Le Soroban et le boulier romain

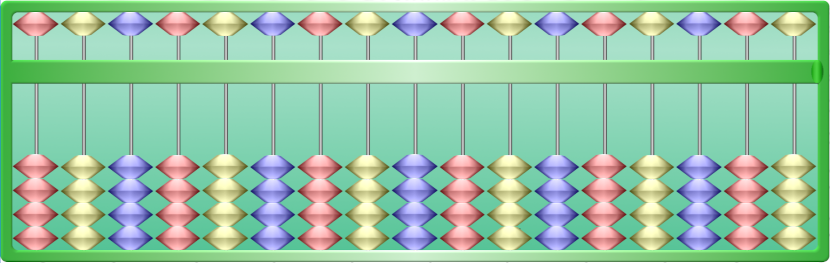
Le Soroban, ou boulier japonais, est la version épurée du Suanpan. Ici, il n’y a plus qu’un seul jeton quinaire par colonne, et 4 jetons unaires au lieu de 5. Ceci n’autorise plus qu’une seule écriture pour chaque nombre. Ainsi, une dizaine ne peut s’écrire qu’à l’aide d’un seul jeton unaire que l’on remonte dans la colonne de dizaine supérieure, contrairement à ce qui se passe avec le Suanpan.

De ce fait, les calculs sont un peu moins naturels, puisqu’il n’est plus possible de procéder aux réductions, comme on pourrait le faire avec les doigts et les mains. Il faut anticiper les réductions.

Notre Soroban possède aussi en exclusivité pédagogique, son séparateur décimal, qui fonctionne sur le même principe que celui du Suanpan.

L’usage du Soroban sera plutôt réservé aux élèves qui savent déjà calculer, pour éveiller leur curiosité et développer leur agilité mentale.

C’est une technique de calcul très efficace et utilisée il y a longtemps déjà, par les Romains.

Un petit tour dans l’antiquité romaine

Actilud propose d’ailleurs une simulation de bouliers romains, toujours dans la partie numération. Ces bouliers fonctionnent sur le principe du Soroban. Pour celles et ceux que cela intéresse, j’ai fait une vidéo qui explique en détail les méthodes de calcul à employer. Cette vidéo explique le fonctionnement du boulier pédagogique romain, qui n’est rien d’autre qu’un Soroban à 4 colonnes (voir la vidéo).

La vidéo explique en particulier comment traiter les passages quinaires et décimaux. Dans le menu du jeu, il y a une entrée qui permet de s’entraîner aux passages quinaires ou décimaux.

Enfin, les curieux trouveront dans le jeu une reproduction de deux bouliers romains, en ivoire et en bronze, utilisables sans contrainte : si vous enseignez les fractions, vous aurez sans doute plaisir à calculer les onces, semunciae et autres duellae, comme le faisaient nos ancêtres.

Le Stchioty

Le Stchioty, ou Stchoty, est le boulier russe. Actilud le propose en deux déclinaisons majeures : avec 10 ou 9 jetons par ligne, et 4 orientations ! selon qu’on souhaite l’utiliser à l’européenne, à la russe, à l’arabe, ou selon ses choix personnels ! Bien sûr, je l’ai un peu adapté. Le nôtre n’a pas de tige à 4 boules, qui était utilisée autrefois (il n’y a pas si longtemps… jusqu’en 1990) pour calculer les quarts de Kopek. Il a aussi gagné son séparateur décimal. La position de départ du séparateur permet de repérer la rangée « unités ».

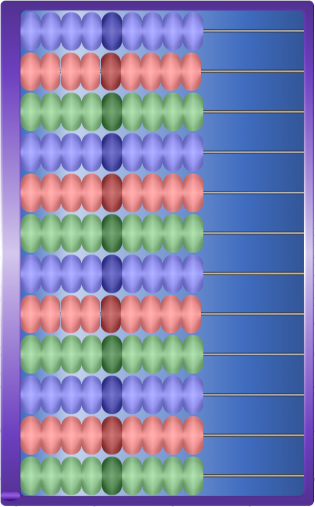
Le Stchioty correspond au boulier de comptage mais avec une algèbre positionnelle. Donc il y a une rangée « unités », une rangée « dizaine », une rangée « centaines » et ainsi de suite.

Chaque jeton a la valeur de sa rangée, toujours des multiples de 10.

Les jetons centraux sont accentués pour bien distinguer les valeurs quinaires.

Le boulier à 10 jetons permet de faire des réductions: lorsque l’on atteint la valeur 10, on replace tous les dix jetons à leur position de départ et on abaisse un jeton de la dizaine supérieure. Le fonctionnement rappelle alors le Suanpan sans les jetons quinaires.

Le boulier à 9 jetons fonctionne davantage comme un Soroban, sans les jetons quinaires bien sûr.

Dans une progression pédagogique, le Stchioty est tout à fait indiqué comme successeur du boulier de comptage.

Les exercices: travailler les entiers ou les décimaux

Outre le travail libre, les exercices permettent de s’entraîner à  :

• représenter des entiers ou des décimaux sur les bouliers
• additionner des entiers ou des décimaux sur les bouliers
• soustraire des entiers ou des décimaux sur les bouliers

Les nombres ont bien sûr une taille limitée par la capacité des bouliers choisis. Si on la juge trop grande, on peut encore la diminuer; il est possible de limiter le maximum à 100 sur tous les bouliers, et à 1000 sur tous sauf le boulier de comptage. Sur les grands bouliers, le plus grand nombre sera 10¹²-1.

Le nombre maximal de décimales est paramétrable aussi, entre 1 et 6.

Il est à noter que l’usage du boulier avec des décimaux oblige à positionner correctement le séparateur décimal. Par exemple, dans le cas suivant : 14,5 + 13,58 l’élève doit se rendre compte, en écrivant le premier nombre, qu’il doit laisser deux positions décimales et non une, sinon il ne pourra pas écrire le second. Bien entendu, le logiciel l’en avertit s’il commet l’erreur. Dans les opérations, le logiciel ne met pas toujours le même nombre de décimales aux opérandes ! C’est ce qui rend l’exercice d’autant plus intéressant.

L’autre intérêt d’utiliser les bouliers avec les nombres décimaux, c’est que c’est la position du séparateur décimal qui détermine la position de l’unité. Je pense que dans la compréhension des nombres décimaux, le fait qu’on puisse écrire le même nombre décimal en plusieurs endroits du boulier, selon la position de la virgule, est un élément déterminant.

Le logiciel en tient compte et accepte toutes les configurations valables, du moment que les nombres sont bien écrits et que les calculs sont faisables.

Pour découvrir comment faire une addition ou une soustraction, vous pouvez vous inspirer de la vidéo sur les bouliers romains. Elle ne traite que du Soroban, en fin de compte, mais l’adaptation aux autres bouliers est assez facile.

Déroulement d’une opération

Dans un premier temps le logiciel indique l’opération qui va être réalisée; c’est une addition ou une soustraction, selon le paramétrage. Il est demandé, à ce stade, de poser le premier nombre. C’est en effet indispensable pour s’assurer que l’opération va bien être effectuée sur le boulier.

Une fois le nombre posé, l’élève doit valider. Si le nombre est exact, on passe à l’étape suivante; sinon, il faut recommencer, mais l’élève bénéficie alors de l’aide du bloc-notes, qui indique la valeur du boulier.

La deuxième étape consiste donc à réaliser le calcul. Ici, la gomme n’efface pas le boulier, mais replace le nombre de départ. C’est pratique en cas d’hésitation, si on souhaite recommencer.

Après d’une première erreur, le bloc-notes devient accessible; l’élève peut alors se rendre compte du résultat. Ce qui ne l’aide pas beaucoup pour le moment, le but étant justement de le calculer. Mais l’élève peut toujours tenter de faire un calcul mental.

Après une seconde erreur, la calculatrice devient accessible. L’élève peut alors tenter de l’utiliser… si le nombre demandé tient sur la calculette ! Celle-ci en effet ne propose que 8 chiffres… Donc, mission impossible dès que l’on rencontre un nombre entier de cent millions ou plus, ou un décimal avec beaucoup de positions après la virgule. Au passage, nous découvrons là la puissance de ces bouliers, capables de dépasser la grandeur et la précision des nombres sur nos calculettes.

Mais cette difficulté n’est pas un réel problème, car le travail sur les très grands nombres n’est proposé -évidemment- que si les élèves parviennent à déjà effectuer des calculs sur des nombres plus accessibles. Leur laisser manipuler de très grands nombres est alors une excellente occasion de dépassement, un défi, que certains apprécieront.

Lien vers la vidéo abaque romain.

Liens vers les jeux :