Des nombres sont cachés et forment un circuit. Chaque nombre est séparé du suivant par une opération. Pour trouver les nombres, il faut que toutes les opérations concordent.

Les règles de base

Les nombres sont tous des entiers naturels compris entre 1 et 100. Cette règle est fondamentale ! Elle permet d’encadrer la recherche.

On utilise les quatre opérations de base : l’addition (+), la soustraction (-), la multiplication (x) et la division (:).

Conformément à la règle, la soustraction doit produire un entier naturel supérieur à 0. Donc, dans l’opération a – b, nous devons avoir a > b.

La division est la division euclidienne sans reste. Autrement dit, pour que la division a : b soit possible, il faut que b soit un diviseur de a.

8 : 2 ok
8 : 3 impossible
8 : 4 ok
8 : 5 impossible

Le circuit est réversible. Il suffit de changer le sens des flèches.  Les “+” permutent alors avec les “-“, les “x” permutent avec les “:”.

Pour provoquer un changement de sens, cliquer sur la double-flèche au centre du circuit.

Bien sûr, les circuits proposés sur Actilud n’ont qu’une seule solution, tant que les nombres sont dans les limites imposées.

Les opérandes

Dans l’addition et la soustraction, l’opérande sera toujours compris entre 1 et 10.

Les multiplicateurs et les diviseurs  sont compris entre 2 et 12.

La stratégie

La première stratégie est d’écrire l’équation correspondant au circuit et de la résoudre ! C’est un exercice très intéressant au collège, mais bien sûr ce n’est pas au programme de l’école primaire. Par exemple, l’équation du circuit ci-dessous est  :

a = 9 (a-2) / 6

ce qui se résout en : a=6

a est le nombre dans la case A

Transformer un circuit en formule n’a rien d’évident ! Il faut respecter la priorité des opérateurs pour écrire les opérations dans le bon ordre.

L’autre stratégie est la “force brute” : essayer tous les nombres les uns après les autres dans une case, les propager, jusqu’à ce que l’on obtienne un résultat cohérent ! Évidemment, si cette stratégie est assez simple à programmer sur un ordinateur, elle n’est guère satisfaisante pour un humain. Elle sera sans doute privilégiée au début par les élèves, surtout si on autorise le calcul des opérations par l’ordinateur.

Voyons donc quelques pistes pour améliorer les performances; notre but étant de développer le sens des opérations !

Définition : a, b, c, … sont les nombres placés respectivement dans les cases A, B, C, …

Trouver l’emplacement du plus petit nombre

Cette piste permet de cibler une case de départ pour nos calculs. Pour cela, nous devons nous demander quelles sont les opérations qui diminuent un nombre dans notre circuit. C’est facile : il s’agit de la soustraction et de la division. Dans le cadre des règles expliquées ci-dessus, dès qu’un nombre est plus grand que 20, la division diminue davantage le nombre que la soustraction;  nous la privilégierons donc, sauf exception. Lorsque plusieurs opérations successives sont des divisions et/ou des soustractions, on peut être à peu près certain que la case d’arrivée de la série contient le nombre le plus petit.

Attention : associer la division à une diminution est vrai dans dans l’ensemble des entiers naturels positifs, si le diviseur est plus grand que 1. Mais ce n’est pas le cas avec des diviseurs réels ou décimaux compris entre 0 et 1 : 20 / 0.5 =40.

Dans une énigme à trois étapes, il est souvent assez facile de trouver la case contenant le plus petit nombre :

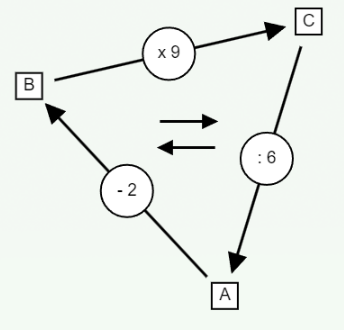
Ici il y a deux opérations successives de diminution :  (: 6) et (- 2). À coup sûr, la case B contient le plus petit nombre. À priori, la valeur minimum de b est 1 et sa valeur maximum est 11, car il est suivi par une multiplication par 9 dont le résultat ne doit pas dépasser 100 : b ∈ [ 1 , 11 ]. Ceci  permet de déduire les valeurs de c et de les écrire par extension : c ∈ { 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99 }.  On peut ensuite utiliser la technique décrite ci-dessous pour découvrir finalement que C doit être multiple à la fois de 9 et de 6, ce qui donne : c ∈ { 18, 36, 54, 72, 90}. Il n’y a plus que 5 possibilités à tester.

Trouver la case qui est multiple des deux cases voisines.

Lorsqu’une multiplication est suivie d’une division, la case à l’intersection des deux opérations doit contenir un multiple qui convienne à la fois à l’une et à l’autre opération.

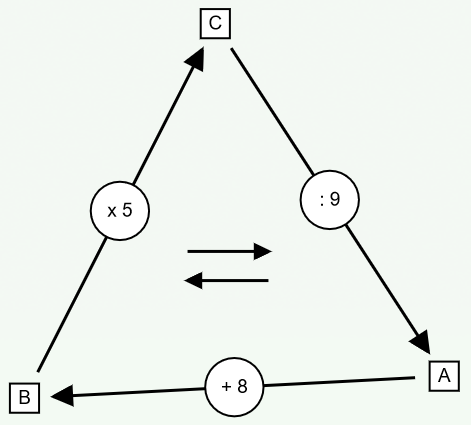
La case C doit être multiple de 5 mais aussi divisible par 9. Il faut donc trouver les multiples communs à 5 et 9; il n’y en a que deux possibles entre 1 et 100 : 45 et 90. Nous n’avons donc que deux tests à effectuer !

Nb: cette technique ne s’applique pas au cas inverse – une division suivie par une multiplication.

Bien observer le circuit et chercher une loi générale

Toujours dans le cadre de la technique de la multiplication suivie par la division, on peut quelquefois limiter le nombre de possibilités en examinant soigneusement le circuit. Dans le cas ci-dessous, nous voyons que la case F contient des multiples de 10 :

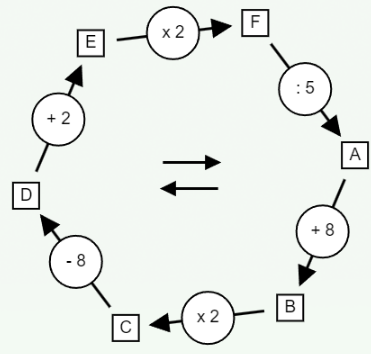
Mais observons bien le chemin qui mène à la case F. Partons de B. Le nombre en B est multiplié par 2, ce qui donne donc un nombre pair en C. Ensuite, on y soustrait 8, mais ce faisant on obtient encore un nombre pair. Puis, on y ajoute 2, ce qui donne toujours un nombre pair. Enfin, ce nombre pair est multiplié par 2. Or, un nombre pair multiplié par 2 donne un multiple de 4 ! Donc, la case en F contient un multiple de 20, ce qui ne laisse plus que 5 cas à examiner, au lieu de 10 : f  ∈ { 20 , 40, 60 ,80, 100 }

Multiples d’arrivée ou de départ

Si dans un circuit, une case est à l’arrivée de plusieurs multiplications consécutives, elle contient un multiple de ces opérations.

Si dans un circuit, une case est le point de départ de plusieurs divisions consécutives, elle contient un multiple de ces opérations.

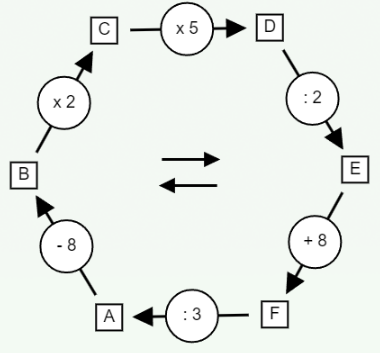
Dans l’exemple ci-dessus, la case D est à l’arrivée de deux multiplication, x2 et x5 : elle contient donc un multiple de 10.

Remarquons aussi, au passage, que la case E contient un multiple de 5 ! En effet, pour parvenir à E à partir de B, la multiplication et la division par 2 s’annulent mutuellement.

Le sens des opérations

Le mot “sens” a un … double sens ! Il s’agit d’une part, de la réversibilité de l’opération (A x B  ⇔ B : A), et d’autre part, de la compréhension de l’opération.

Dans l’exemple ci-dessus, on voit que l’on inverse souvent les calculs: dans l’exemple 1, pour aboutir à la case A à partir de C, on fait une division. Mais pour retrouver C à partir de A, on fait donc une multiplication.

Pour bien maîtriser les opérations, il faut donc utiliser réversibilité.

Mais ce n’est pas suffisant. Il faut aussi comprendre et utiliser les notions de diviseur et de multiple. Si on reconnaît un multiple ou un diviseur d’un coup d’œil, on évite bien des calculs. La connaissance des tables de multiplication est ici très importante.

Une façon simple d’aborder les notions de diviseurs et de multiples est d’utiliser ce que les élèves connaissent déjà : les tables de multiplication. Il suffit de leur faire remarquer que toute multiplication peut s’écrire sous la forme : diviseur1 x diviseur2 = multiple.

Il est impératif d’utiliser un support pour écrire les hypothèses; sinon, on risque de tâtonner sans grande efficacité. On gagne du temps si on écrit les intervalles pour les nombres consécutifs, ou des ensembles extensifs de nombres possibles à barrer au fur et à mesure.

Lorsque les grilles ont plus de 3 cases, c’est plus difficile, mais on peut procéder de même, de proche en proche.

Des opérations automatiques au calcul mental

Par défaut, après avoir déposé une étiquette sur une case, on peut cliquer sur l’opération correspondante. Celle-ci est automatiquement effectuée et le résultat, une nouvelle étiquette, se dépose dans la case suivante. Si jamais il y avait déjà une étiquette différente dans cette case, celle-ci est déplacée sur le côté, ce qui permet d’en conserver le souvenir.

L’opération automatique permet aux élèves de se concentrer sur l’essentiel, la découverte d’une stratégie sans être perturbé par les calculs. Je recommande cette approche au tout début. Elle permet à tous de bien comprendre ce qu’il se passe, grâce aux animations des étiquettes. On peut aussi retourner les flèches, l’action est visuelle et montre bien que le sens des opérations change, et que les opérations elles-mêmes  permutent.

Bien sûr, les opérations automatiques sont des béquilles qui, à terme, risquent de diminuer l’efficacité de la recherche ! Dans un second temps, on peut inhiber les opérations automatiques, tout en conservant la possibilité de faire des calculs avec la calculette – ce qui est déjà plus fastidieux et incite les élèves à calculer mentalement les opérations simples.

Enfin, une fois les élèves entraînés, on interdit toute aide (à part le brouillon, bien sûr), pour favoriser le calcul mental.

Dans tous les cas, il est conseillé d’apporter un cahier de brouillon. À défaut, on peut utiliser la fenêtre de notes prévue à cet effet.

Le calcul mental, cela s’apprend !

À tout hasard, voici un petit rappel utile de ce que les élèves devraient savoir.

Bien connaître ses tables d’addition et de multiplication.

Cela tombe sous le sens. Pas de calcul mental efficace sans cela. Le jeu est aussi un bon moyen de s’entraîner si on supprime l’aide automatique.
Il est recommandé de connaître aussi la table de 11 jusqu’à 99 (ce qui est facile) et la table de 12 (pas si facile mais tellement utile.)

Savoir identifier la divisibilité

Voici un petit rappel des techniques qui, lorsqu’elles ne sont pas universelles, sont applicables à des nombres jusqu’à 100.

divisible par 2 : le nombre doit être pair  (règle universelle.)

divisible par 3 : faire la somme de tous les chiffres du nombre. Les chiffres 9 peuvent être remplacés par 0.  Si le résultat est un nombre à plusieurs chiffres, on recommence l’opération sur le résultat jusqu’à obtenir un seul chiffre.  À la fin, le nombre obtenu doit être 0, 3, 6 ou 9, c’est à dire multiple de 3  (règle universelle.)

124932 :
1 + 2 = 3
3 + 4= 7
7 + 9 ⇔ 7 + 0 = 7
7 + 3 = 10, 1 + 0 = 1
1 + 2 = 3
124932 est multiple de 3

divisible par 4 :  les deux derniers chiffres forment un nombre lui-même divisible par 4. Comme on n’apprend la table de 4 que jusqu’à 40, on peut soustraire 40 ou 80 au nombre formé par les deux derniers chiffres si celui-ci est trop grand, avant de vérifier la divisibilité par 4 (règle universelle).

2576 est-il divisible par 4 ?
76 – 40 = 36
36 est divisible par 4 => 2576 est divisible par 4

divisible par 5 : le nombre se termine par 0 ou 5 (règle universelle).

divisible par 6 : le nombre doit être pair et divisible par 3 (règle universelle)

divisible par 7 : le nombre doit figurer dans la table de 7. S’il est plus grand que 70, lui soustraire d’abord 70.
Il existe une technique universelle, peu connue, qui n’est généralement pas enseignée car trop complexe. On retire le dernier chiffre du nombre, on le double et on le soustrait au nombre tronqué. On recommence tant que c’est possible. A la fin, on vérifie si le résultat est dans la table de 7.

2401 est-il divisible par 7 ?
On retire le 1, il reste 240
240 – (1×2) = 240-2 = 238
On retire le 8, il reste 23
23 – (8×2) = 23 – 16 = 7 présent dans la table de 7
2401 est divisible par 7

divisible par 8 : pas de technique particulière; si le nombre est impair, il n’est pas divisible par 8. S’il est pair, il doit figurer dans la table de 8. Soustraire 80 s’il est plus grand.

divisible par 9 : utiliser la règle de la divisibilité par 3. Si le résultat est 0 ou 9, le nombre est divisible par 9 (règle universelle).

divisible par 10 : le nombre finit par un 0 (règle universelle).

divisible par 11 : le nombre (plus petit que 100 !) est formé de deux chiffres identiques : 11, 22, 33, 44, etc.

divisible par 12 : pas de technique particulière; vérifier si le nombre est pair. Si c’est le cas, vérifier qu’il figure dans la table de 12.