Disponible dans la partie Énigmes de logique, le jeu Admission à l’académie Gorgias associe la lecture à la logique. Pour résoudre les énigmes proposées, il faut bien lire l’énoncé et surtout, analyser les propositions qui sont faites et les classer en fonction du nombre de menteurs.

Le principe

Le joueur vit en Grèce, en l’an 450 avant notre ère. Il souhaite entrer à l’académie Gorgias, où l’on enseigne, entre autre choses, la Logique. Il subit un examen d’entrée. Dans chaque salle d’examen, ses professeurs, les académiciens, lui proposent de choisir une boule numérotée et de la déposer dans une urne. Une seule de ces boules permet d’avancer dans le jeu. Les autres conduisent à l’échec.

Le joueur dispose de deux indications :

• le nombre de menteurs, indiqué dans l’énoncé
• les propositions des académiciens

Certaines de ces propositions sont vraies et d’autres sont fausses. Le nombre de propositions fausses correspond au nombre de menteurs. Pour s’en sortir, le joueur doit :

• classer les académiciens en menteurs et “véridiques”, en les plaçant sur la zone “vrai” et la zone “faux”.
• trouver la bonne boule numérotée et la déposer dans l’urne

Si les deux conditions sont remplies, le joueur avance vers une nouvelle salle, qui contient un académicien de plus. S’il échoue, il perd un point et recommence dans la même salle. Le jeu s’arrête lorsqu’il n’y a plus de points; néanmoins, il y en a largement assez pour pouvoir avancer sans être inquiété.

Quelques remarques historiques

Gorgias  vécut très vieux (108 ans) et avait une trentaine d’années en 450 av. n.è., date de notre énigme. S’il n’a vraisemblablement jamais fondé d’académie, il eut de nombreux élèves qui payaient fort cher pour son enseignement de la rhétorique. Dans son traité sur le non-être, il démontre, ou tente de démontrer,  par un raisonnement logique, qu’il n’y a pas d’ontologie possible, ce qui évidemment n’était pas du goût de Platon qui l’a largement dénigré et avec lui toute la sophistique.

Si vous observez les académiciens, qui sont tirés aléatoirement, vous verrez qu’il y a des hommes, certes, mais aussi des femmes. Ici bien sûr, il n’y a pas de respect de la vérité historique ! c’est un ajustement aux réalités contemporaines !

Vérité, mensonge et injonction

Si on analyse les propos des académiciens, on découvre qu’ils sont de deux sortes.

• les propositions : “La boule 2 amène l’échec”
• des injonctions, qui ne sont pas, à proprement parler, des propositions : “Ne choisis pas la boule 3 !”

Une proposition, en logique, est un énoncé qui peut être vrai, ou faux. Or une injonction n’est pas une proposition, c’est un ordre qui, à priori, ne peut être vrai ou faux. Toutefois, si on lit attentivement l’énoncé introductif, on sait qu’il faut “répartir les académiciens entre les menteurs, qui souhaitent l’échec du joueur, et ceux qui disent la vérité, qui souhaitent son succès.”

Dans le cas général, il y a une indépendance entre la volonté d’aider ou de nuire, et celle de dire la vérité ou de mentir. En effet, on pourrait imaginer une énigme où ce sont les menteurs qui veulent aider le joueur ! Donc la phrase d’introduction est extrêmement importante, car c’est elle qui permet de fixer un statut de vérité ou de mensonge aux injonctions.

Pourquoi ai-je mis des injonctions ? Tout simplement pour varier un (tout petit) peu la lecture.

Si on a des élèves, il est important de bien leur faire comprendre le rôle des introductions, dans les problèmes de logique.

Deux niveaux d’interprétation

Pour rendre l’analyse un peu plus difficile, on peut choisir le niveau “difficile” dans le paramétrage, interprétation des phrases. Dans ce niveau de difficulté, certains académiciens font référence aux propos d’autres académiciens. Il faut alors transformer leurs propos pour qu’on puisse les résoudre.

Alpha dit: “Je suis d’accord avec Omicron”.
Omicron dit: “Choisis la boule 5 !”

Il faut transformer la proposition d’Alpha. Il est d’accord avec Omicron, donc cela signifie qu’il dit la même chose qu’Omicron: “Choisis la boule 5 !”. On peut à ce moment appliquer un statut de vérité ou d’erreur à ces propositions.

Alpha dit: “Je suis d’accord avec Omicron” ⇒ “Choisis la boule 5 !”.
Omicron dit: “Choisis la boule 5 !”

Voici un autre cas :

Alpha dit : “N’écoute pas Omicron !”
Omicron dit : “Ne choisis pas la boule 3 !”

Ici Alpha n’est pas d’accord avec Omicron. En effet, il recommande de ne pas l’écouter. Il faut donc dire le contraire d’Omicron Après transformation, cela donne :

Alpha dit : “N’écoute pas Omicron !” ⇒ “Choisis la boule 3 !”
Omicron dit : “Ne choisis pas la boule 3 !”

Trouver les “véridiques” et les menteurs : rester cohérent

C’est la partie la plus intéressante de notre énigme. Au départ, tous les académiciens sont placés sur la zone “véridique” :. La zone des menteurs, , est vide.

 

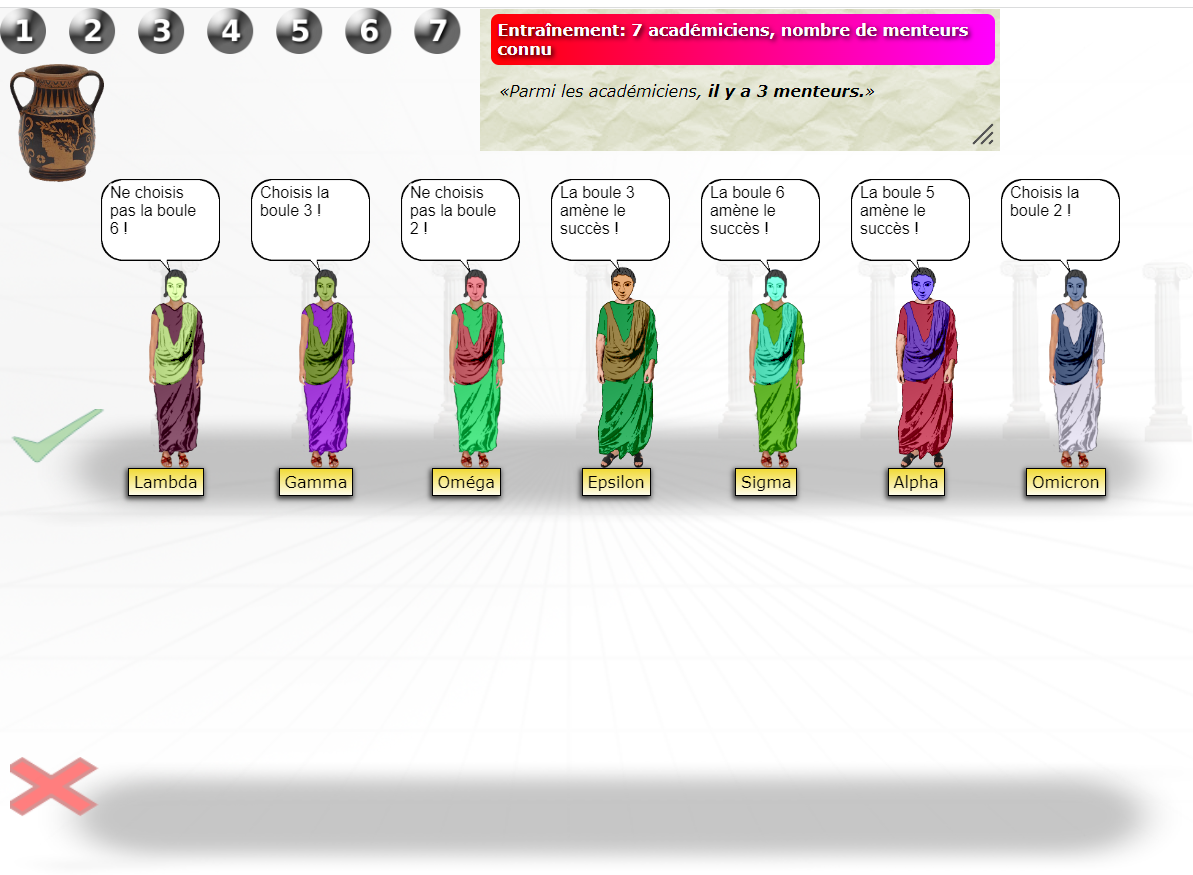
Dans l’illustration, il y a trois menteurs. Il faut donc déplacer trois académiciens dans la zone . Mais comment procéder ? En rendant l’énoncé cohérent.

La cohérence, c’est la clé

D’après l’énoncé introductif nous savons trois choses :

• il y a une solution
• cette solution est unique
• il y a trois menteurs

Il y a une solution, donc nous pouvons résoudre l’énigme et nous pouvons rejeter une réponse qui ne propose aucune boule “gagnante”.

La solution est unique, donc nous devons rejeter toutes les réponses qui produisent plusieurs boules “gagnantes”.

Il y a trois menteurs: donc il faut trois académiciens dans la zone du bas.

Comment rendre l’énoncé cohérent ? en regroupant les énoncés qui parlent de la même boule et en inversant les propositions des menteurs.

Inverser les propositions

Voici comment cela se passe pour le deuxième académicien, Gamma :

Elle dit : “Choisis la boule 3 !” qu’on traduit par : “La boule 3 amène le succès !”.
Si elle ment, sa proposition devient :  “La boule 3 amène l’échec !”

Regrouper les énoncés qui parlent de la même boule

Nous constatons en observant attentivement l’énigme ci-dessus, qu’il y a un problème avec la boule 2.

Oméga : “Ne choisis pas la boule 2 !” ⇒ “La boule 2 amène l’échec.”
Omicron : “Choisis la boule 2 !” ⇒ “La boule 2 amène le succès”.

L’un des deux ment, forcément.

Si Oméga est le menteur, alors Omicron dit la vérité. Donc la boule 2 conduit à la réussite. Mais l’énoncé indique aussi que la boule 3, la boule 5 et la boule 6 conduisent à la réussite. Or nous savons qu’il ne peut y avoir qu’une seule boule. Si nous maintenons malgré tout qu’Oméga est un menteur, il y faut qu’il y ait 5 menteurs pour que la solution devienne cohérente : “La boule 3 amène le succès” (deux menteurs), “La boule 6 amène le succès”, “La boule 5 amène le succès” et bien sûr “Ne choisis pas la boule 2”. Or, ce nombre de menteurs ne correspond pas à la donnée de l’énoncé: il en faut 3. Nous pouvons donc dire avec certitude qu’Oméga dit la vérité et qu’Omicron fait partie des menteurs.

De fil en aiguille, en déplaçant les figurines dans les zones, on finit par trouver une solution cohérente : les menteurs sont les trois derniers (Sigma, Alpha, Omicron) Il en résulte un seul conseil, porté par deux académiciens : celui de choisir la boule 3.

 

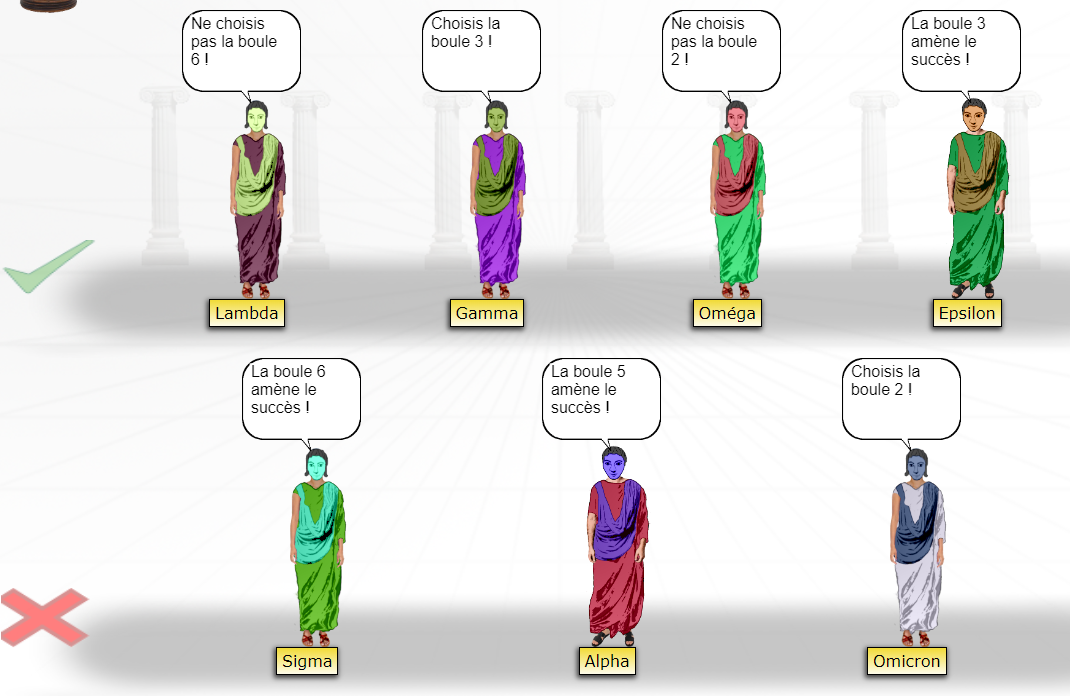
Quelquefois, le N° de la boule gagnante n’apparaît pas directement. Il faut éliminer toutes les boules perdantes et constater qu’il ne reste plus qu’une seule boule disponible, qui forcément, est la gagnante.

 

Les deux menteurs sont Epsilon et Alpha. On ne peut donc choisir ni la boule 2, ni la 4, ni la 1. Il reste donc la boule 3 qui est la solution.

Comme il existe une solution unique, inutile de chercher d’autres possibilités. Une fois qu’on a trouvé une solution, c’est forcément la bonne !

Nombre de menteurs inconnu !

La fin l’énigme se corse ! Nous savons qu’il existe une solution unique mais on ignore le nombre de menteurs !

Alors comment faire ?

La cohérence, encore et toujours

Il va falloir passer en revue toutes les possibilités. Heureusement, dans le parcours du débutant et pour un nombre de menteurs inconnu, il n’y a que 4 académiciens au maximum ! Pour quatre académiciens, il peut donc y avoir 0, 1, 2, 3 ou 4 menteurs.

Pour déterminer le nombre de menteurs, il faut tester, pour chaque nombre de menteurs, s’il existe une solution unique. S’il n’y a pas de solution, ou s’il y en a plusieurs, alors on élimine le nombre de menteurs et on passe au suivant.

Un cas simple pour commencer

Oméga : la boule 2 amène l’échec.
Alpha: Ne choisis pas la boule 2 !
Omicron: Ne choisis pas la boule 2 !
Sigma: Ne choisis pas la boule 2 !

Observons l’illustration ci-dessus. Il semble que nos académiciens se soient mis d’accord : il ne faut -surtout- pas prendre la boule N° 2 ! C’est bon signe: l’énigme sera facile.

0 menteur

Situation très intéressante. Tout le monde dit la vérité, donc il ne faut pas prendre la boule 2. Mais nous ne savons pas pour autant quelle boule prendre ! Avec 0 menteur, nous voyons bien qu’il y a trois boules possibles -la 1, la 3 et la 4. Ce qui est en contradiction avec l’énoncé d’introduction : une seule boule conduit à la liberté. Donc, disposant de trop de solutions ce qui nous interdit de conclure, nous en déduisons qu’il n’y a pas de solution unique – comme stipulé dans l’énoncé. Comme on nous dit qu’il existe une solution unique, il n’y a pas 0 menteur.

1 menteur, 2 menteurs, 3 menteurs :

Aucun de ces cas n’est possible ! Comme ils disent tous la même chose… Ils ne peuvent que dire la vérité -ce qui n’est pas possible, comme on l’a vu- ou mentir, tous ensemble. Avec ces nombres de menteurs, il y a toujours une contradiction. Or, on doit rester cohérent. Quand je vous disais que l’énigme sera facile !

4  menteurs : bingo  !

Ils mentent tous. Donc il faut déplacer tout le monde sur la ligne , prendre la boule 2 et la déposer dans l’urne. Et voilà !

Un cas un peu plus complexe pour continuer

Encore des académiciens qui parlent de la même boule, mais cette fois ils ne sont pas d’accord.

 

Oméga: la boule 3 amène le succès !
Omicron: Ne choisis pas la boule 3 !
Sigma: choisis la boule 3 !
Lambda: La boule 3 amène l’échec !

Deux académiciens disent qu’il ne faut surtout pas prendre la boule 3. Deux autres, au contraire, prétendent qu’il faut bien la prendre.

Là, au moins, il est facile de trouver le nombre de menteurs ! Il ne peut y en avoir que 2, si on veut éviter les contradictions. De plus, les menteurs vont par paire : les menteurs sont soit Oméga et Sigma, soit Omicron et Lambda. Tout autre combinaison de deux menteurs conduit à une contradiction.

Menteurs Oméga et Sigma

Si Oméga et Sigma sont les menteurs, nous savons qu’il ne faut pas choisir la boule 3. Très bien. Mais quelle boule choisir ? Nous ne pouvons pas le déterminer avec certitude. Nous nous retrouvons dans le cas précédent. Il n’y a pas de solution unique. Donc les menteurs ne peuvent pas être Oméga et Sigma.

Menteurs Omicron et Lambda : bingo !

Eh oui, les menteurs, les voilà ! Du coup nous savons qui il faut déplacer sur la ligne , et nous savons qu’il faut placer la boule 3 dans l’urne : c’est bien la seule et unique solution de l’énigme.

Un autre cas d’école

Voyons la situation suivante :

 

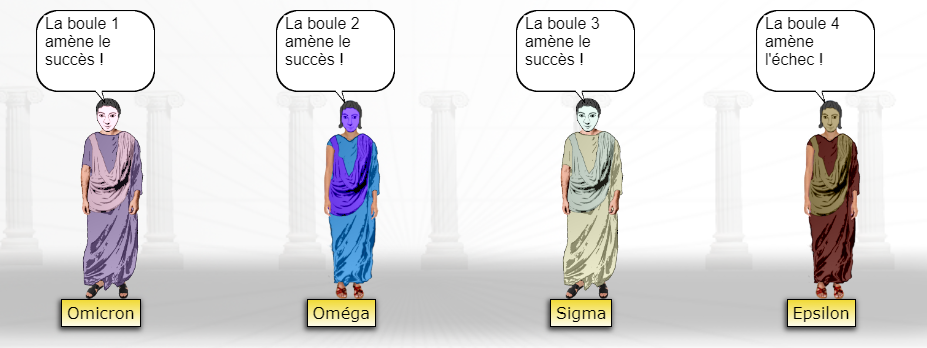
Omicron: La boule 1 amène le succès !
Oméga: la boule 2 amène le succès !
Sigma: la boule 3 amène le succès !
Epsilon: la boule 4 amène l’échec !

Ici, avec un peu d’habitude, on voit que la solution c’est 4 menteurs. En effet, pour ce nombre de menteurs, il n’y a qu’une seule solution possible – prendre la boule 4. C’est la solution unique demandée. C’est suffisant pour résoudre l’énigme, on n’a pas besoin de chercher plus loin.

Toutefois, voyons ce qu’il se passe avec les autres nombres de menteurs. Histoire de prouver que l’énigme est cohérente, et surtout pour découvrir quelques cas intéressants.

0 menteur

Pas possible : si tout le monde dit la vérité, il y a trois boules à choisir alors qu’il n’en faut qu’une.

1 menteur

Quel que soit le choix du menteur, il reste toujours plusieurs boules à choisir. Donc aucune solution n’est envisageable.

2 menteurs

Là ce qu’il se passe est intéressant.

Si les deux menteurs sont Omicron et Oméga, il faut choisir la boule 3. La réponse est cohérente et pourrait être une solution.
Si les deux menteurs sont Omicron et Sigma, il faut choisir la boule 2. Là encore, la réponse est cohérente, mais elle est  une nouvelle solution pour 2 menteurs.
Si les deux menteurs sont Oméga et Sigma, il faut choisir la boule 1. Encore une réponse cohérente, mais cette fois c’est une troisième solution pour 2 menteurs.

Nous avons trouvé trois solutions pour deux menteurs. Les autres réponses, impliquant Epsilon comme un des deux menteurs, amènent toutes à des réponses avec plusieurs boules.

Nous pouvons donc exclure le cas de deux menteurs, car il pourrait y avoir plusieurs solutions – or nous savons qu’il faut une solution unique.

3 menteurs

Si les trois menteurs sont Omicron, Oméga et Sigma, on ne peut plus choisir de boule. La réponse est donc rejetée.
Il faut donc toujours inclure Epsilon parmi les menteurs. De ce fait, on obtient des réponses où il y a deux boules à choisir. Ce n’est pas possible car il faut une solution unique.

Jeu ou entraînement

Par défaut le logiciel propose de démarrer le parcours en plusieurs étapes. Toutefois, on peut s’entraîner en choisissant soi-même le nombre d’académiciens, dans l’entrée Jeu des paramètres.

Logique et lecture

On le voit, le joueur est actif devant son énoncé. Il doit transformer certaines propositions en leur contraire, selon le nombre de menteurs; ensuite, il doit vérifier la cohérence globale de sa réponse, et tester, dans les cas les plus difficiles, si elle est unique. La logique ici, offre aux élèves un moyen pertinent et ludique de travailler un énoncé sans faire de calcul. C’est une excellente préparation à la lecture des énoncés mathématiques et une très bonne formation à la rigueur et à la logique.

Entrer dans le jeu