Soit une alternative formée de n booléens. Toute case se situant à l’intersection des n booléens de l’alternative est fausse.
La technique est simple lorsqu’elle s’applique dans une seule grille. C’est d’ailleurs ce qui motive la création de cette règle.
Lorsqu’elle s’applique à des grilles différentes, la technique est une reprise de la fusion avec des booléens formant une alternative.
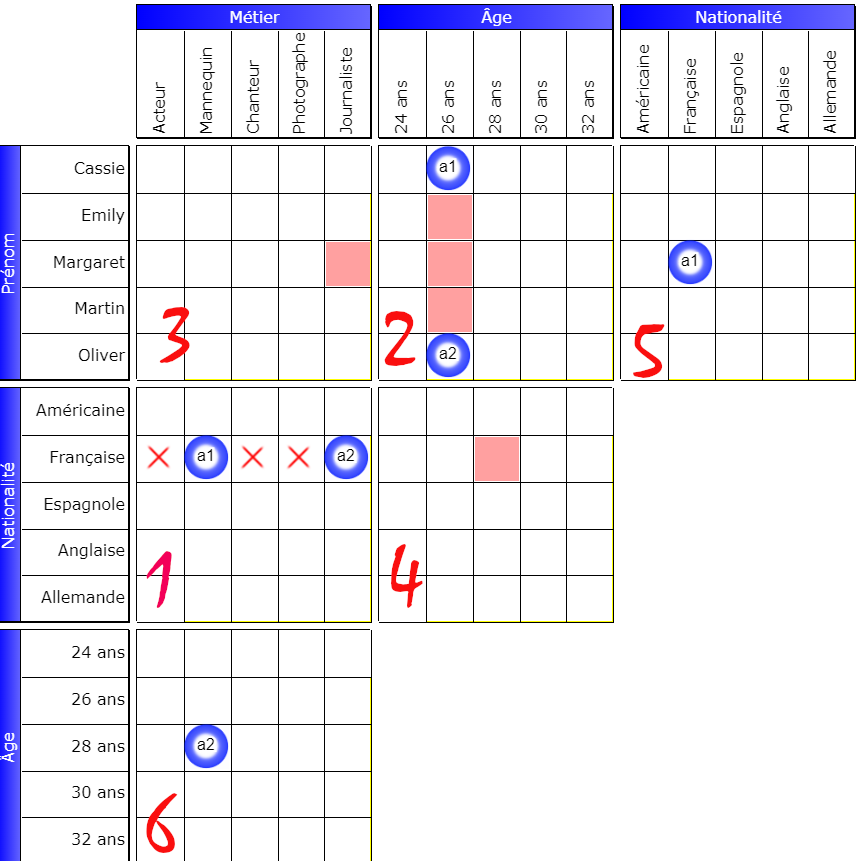
Dans la grille marquée 1, il y a une alternative: la personne française est soit mannequin, soit journaliste, ce qui est matérialisé par les booléens a1 et a2. Nous avons donc a1 ≠ a2.
Les booléens a1 et a2 sont dispersés sur les autres grilles.
Dans la grille N°2 on voit que toutes les cases à l’intersection de a1 et de a2 sont fausses. C’est normal puisque a1 et a2 forment une alternative définie dans la grille 1.
Les choses sont plus subtiles dans la grille 3 et la grille 4. Appliquons les techniques de fusion.
Dans la grille 3, Margaret ne peut pas être journaliste. Si nous fusionnons la ligne contenant a1 dans la grille 5 avec la colonne contenant a2 dans la grille 1, nous découvrons que a1=a2. Or comme a1 ≠ a2, la fusion n’est pas possible et donc la case pivot (Margaret, journaliste) est fausse.
Dans la grille 4, l’invité de nationalité française ne peut avoir 28 ans. Fusionnons la ligne contenant a2 de la grille 6 (ligne 28 ans) avec la ligne contenant a1 de la grille 1 (ligne française). Là encore a1=a2 ce qui n’est pas possible et donc, la case pivot (française,28 ans) est fausse.
C’est le même principe avec l’énigme suivante :

Toujours en appliquant les techniques de fusion, on découvre que les cases pivot (Cassie, Acteur) et (Margaret, Photographe) sont nécessairement fausses.
Pour repérer facilement ces cas, observez les rangées contenant les mêmes booléens, repérez les en-têtes communs et trouvez les pivots : ici l’en-tête commun est Française.
Dur, dur… un peu d’invariance
Il existe des cas d’intersection plus difficiles à trouver. Voyez le cas de la grille ci-dessous, tirée de l’énigme “au verger”. J’y ai vidé toutes les cases, sauf celles utiles à mon propos.
Ces cas d’intersection relèvent en fait de l’invariance, technique avancée qui est décrite dans un autre chapitre. Mais il s’agit d’un cas d’invariance très simple, c’est pourquoi le solveur est capable de le révéler en traitant les intersections, lorsqu’il a affaire à des alternatives à deux booléens.
Observez la grille ci-dessous.
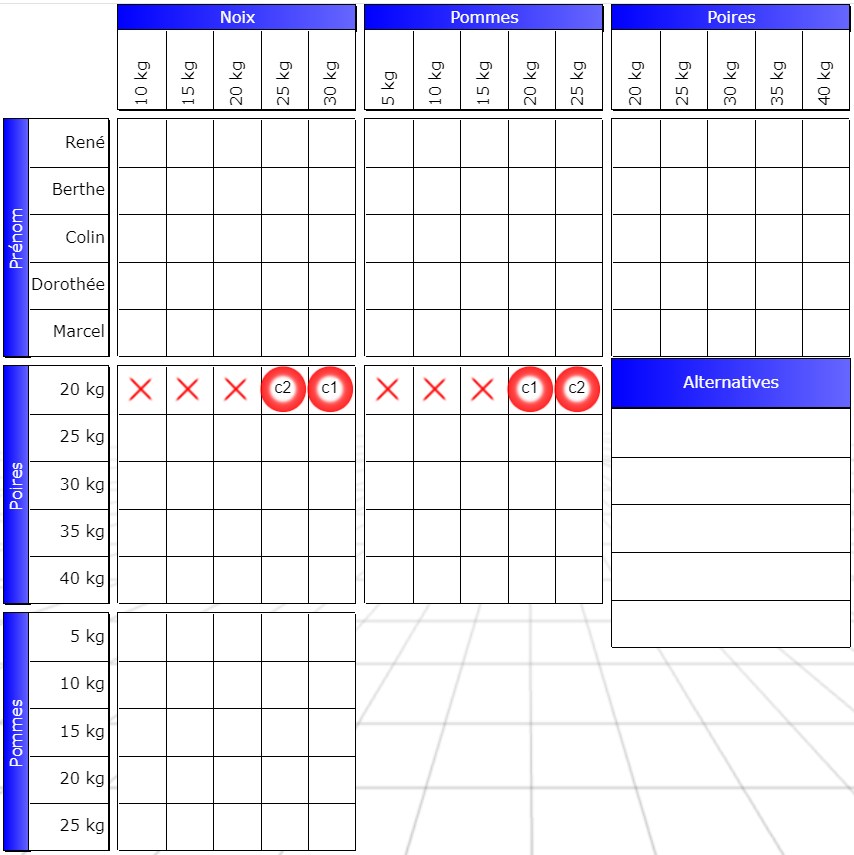
Il y a deux cases toujours fausses. Les voyez-vous ?
Pour les trouver, il suffit de se demander ce qu’il se passe si c1 est vrai, puis ce qu’il se passe si c2 est vrai. Nous découvrons alors deux cases qui sont toujours fausses. Si vous ne les avez pas trouvées, prenez un peu le temps de les découvrir avant de lire la suite.
Voici la réponse :
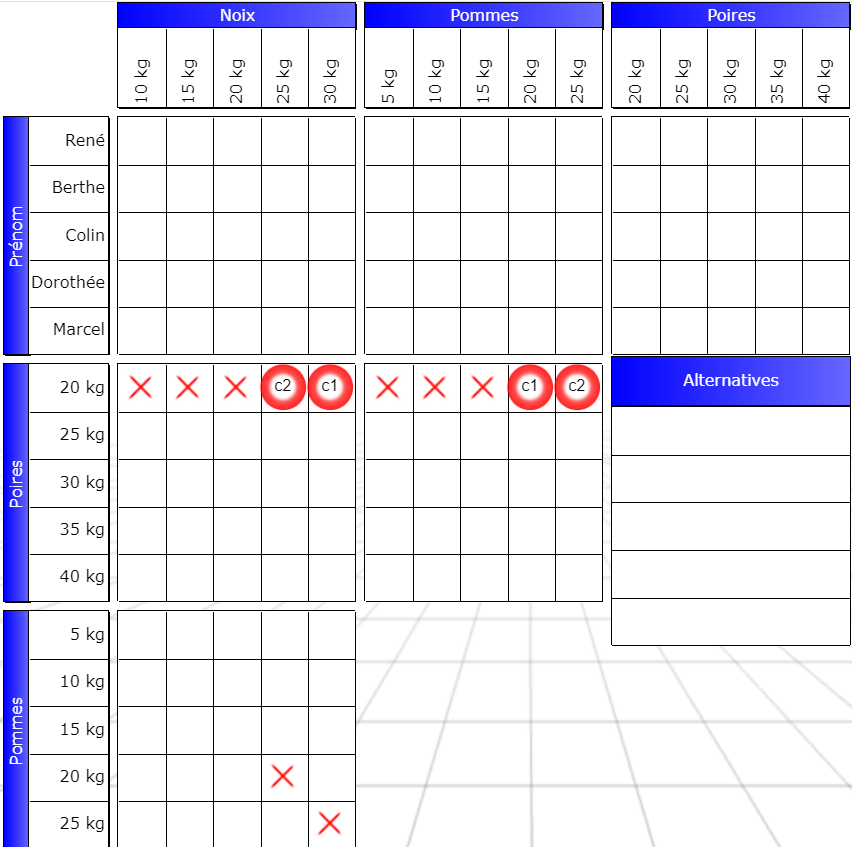
Il existe un moyen plus simple de découvrir ces cases. En utilisant l’intersection, justement.
Notons d’abord que c1 et c2 forment une alternative. L’un est vrai, l’autre est faux. Au lieu de reporter les signes vrai dans la grille “pommes” du bas, reportons plutôt les booléens c1 et c2, selon que l’un ou l’autre est vrai. Si c1 est vrai, il se retrouvera vrai dans la ligne “pommes, 20kg”. Si c2 est vrai, il se retrouvera vrai dans la ligne “pommes, 25kg”.
Nous reproduisons ici seulement le bas de la grille :
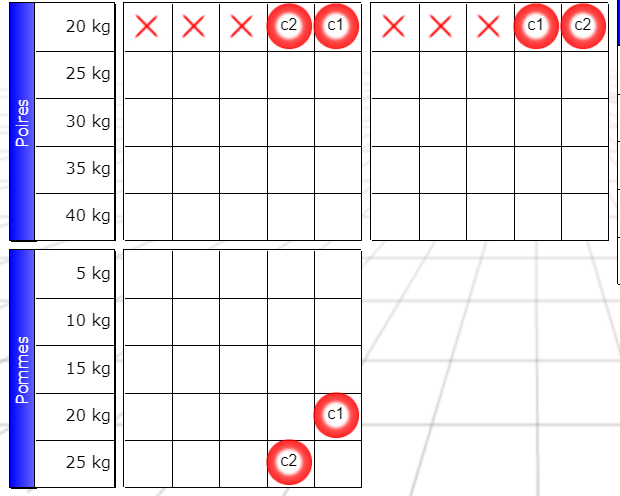
C’est une forme de répercussion que nous n’avons pas encore étudiée.
Il suffit maintenant de leur appliquer l’intersection :
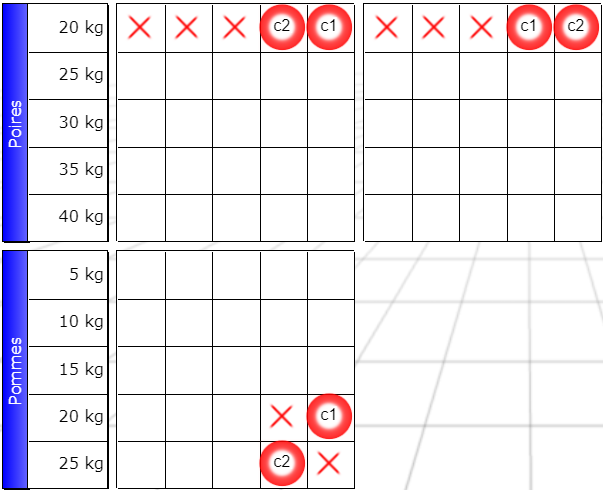
Vous pouvez laisser les deux booléens en place. Le solveur le ne fait pas : il se contente de mettre les signes faux en place, sans répercuter les booléens.
