Apprendre à compter, découvrir le nombre : le domino à numération décimale peut apporter une aide visuelle dans cet apprentissage. Cet article explique les principes pédagogiques mis en œuvre avec cet outil et propose quelques activités.
Avertissement
Les indications pédagogiques données ici sont générales. Que vous les mettiez en œuvre avec le domino ou non, vous pouvez les appliquer à toutes les autres situations de comptage.
Le domino décimal décrit ici est une des activités que l’on peut proposer aux élèves, parmi les autres, en maternelle jusqu’au CP au moins. Il faut moduler les activités en fonction de l’âge des enfants et éviter la précipitation. Parents, n’allez pas trop vite, cela peut être préjudiciable !
Les différents aspects d’un nombre
L’aspect nominal
Ce sont les signes, graphiques ou sonores, que l’on utilise pour représenter un nombre. Le signe 7 s’écrit en Français « sept » et se prononce [sɛt]. L’aspect nominal dépend des conventions locales et de la langue employée – par exemple en Birman on l’écrit ၇.
Il y a de nombreuses représentations possibles. Le domino ci-dessous est une autre représentation conventionnelle du nombre 7.
 L’aspect cardinal
L’aspect cardinal
C’est l’aspect le plus courant : un nombre est utilisé pour représenter une quantité d’éléments dans un ensemble.
Il y a 7 vélos sous le préau.
L’aspect ordinal
Il est assez facile de comprendre cet aspect lorsqu’on étudie une langue et que l’on apprend les adjectifs numéraux ordinaux : premier, second, troisième, quatrième… Lorsque l’on apprend à compter, souvent on simplifie en remplaçant les adjectifs numéraux par leurs substantifs: un, deux, trois, quatre…, utilisant ainsi la comptine numérique. L’aspect ordinal, c’est donc la position d’un élément dans une série ordonnée d’éléments où chaque élément possède un numéro d’ordre.
Le comptage : numérotage et dénombrement
Compter met en œuvre les trois aspects décrits ci-dessus. L’aspect nominal lorsqu’on utilise un signe pour identifier le nombre – que ce signe soit un chiffre, un mot écrit ou prononcé. L’aspect cardinal lorsque l’on trouve la quantité d’éléments – le cardinal de l’ensemble. L’aspect ordinal dans la stratégie mise en œuvre pour compter. En effet, pour compter il faut ordonner une série, même si les éléments qui la composent sont tous identiques et placés pêle-mêle. Si je dois compter le nombre de billes dans un sac, je peux les extraire une à une et les placer dans un récipient, créant donc un ordre artificiel et profitant de cette action pour les dénombrer. Il en va de même pour nos jetons.
On distingue le comptage-dénombrement et le comptage-numérotage (Rémi Brissiaud).
Le comptage-numérotage est couramment utilisé dans les familles. On désigne les objets un à un et on les numérote. On récite ainsi la comptine numérique et on s’arrête sur le dernier objet – le dernier numéro exprimant donc le nombre d’objets. Mais on opère là un glissement de sens, entre la numérotation d’un objet et l’expression d’une quantité d’objets. Quand on procède ainsi, les jeunes enfants n’associent pas le nombre prononcé à la quantité d’objets de la collection, mais à l’objet compté lui-même. Ceci peut créer des problèmes importants dans la compréhension du nombre.
Pour assimiler correctement la mesure de la quantité, il est important de procéder par comptage-dénombrement, par itération de l’unité.
Le domino à numération décimale et le comptage itératif
Le domino à numération décimale est un outil parmi d’autres que l’on peut utiliser pour apprendre à compter. Cet outil ne doit pas être le seul, bien entendu, et ne doit pas remplacer la manipulation d’objets réels. Cependant, son automatisation permet de varier l’enseignement en apportant un petit « plus » visuel : le déplacement automatique des jetons dans le domino. L’idéal est d’utiliser un tableau numérique interactif plutôt qu’un simple vidéo-projecteur, car le geste est très important, il fait partie de la procédure de comptage, et pour cela il doit être vu : il s’agit de le théâtraliser. Si on a la chance d’en avoir, on réservera les tablettes pour le travail individuel ou en petit groupe.
Paramétrage : travail libre, mode « unité » et une seule barre (1,1,1,-)
On peut placer des jetons un à un dans le domino affiché. Remarquez le sélecteur, à gauche : il contient un jeton-unité, mais aussi une pile de 10 jetons et une pile de 5. On y reviendra.
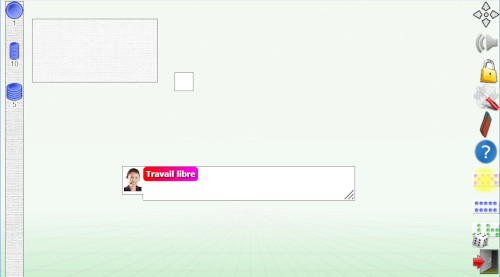
Utilisons le comptage-dénombrement. Voici un exemple possible de présentation de l’activité.
Plaçons le premier jeton. Le prendre dans le sélecteur, le déplacer dans le domino, puis dire « Il y a un jeton ».
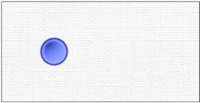
Prendre un autre jeton dans le sélecteur, le déplacer, le lâcher dans le domino. Là, dire « et encore un… 2 ». Notez que « et encore un » peut être prononcé lorsque l’on saisit le jeton dans le sélecteur. Mais pour prononcer le 2, il faut attendre que le jeton ait trouvé sa place dans le domino (important). En procédant ainsi, on fait comprendre que ce n’est pas le jeton « deux » (cardinal) que l’on prend, mais bien le deuxième (ordinal); le jeton déplacé étant assimilé à l’unité (« et encore un« ).
 Poursuivez par « et encore un… 3 ». Et ainsi de suite.
Poursuivez par « et encore un… 3 ». Et ainsi de suite.
Ce faisant, on décrit l’action d’ajouter le jeton au domino, ainsi que le résultat de l’opération (le cardinal de l’ensemble) dans une seule et même phrase, très simple au demeurant.
Bien sûr, on arrêtera le comptage en fonction de l’âge des enfants. Pour les petits (3/4 ans), aller jusqu’à 3 ou 4 c’est très bien !
Les trois modes de représentation des jetons dans les dominos
![]()
Le mode standard, avec une représentation classique des nombres en deux parties de 5.
![]() Le mode « colonnes » ou les nombres sont répartis deux par deux, de haut en bas, dans 5 colonnes.
Le mode « colonnes » ou les nombres sont répartis deux par deux, de haut en bas, dans 5 colonnes.
![]() Enfin,le mode aléatoire ou les dix positions sont choisies au hasard. On peut cliquer plusieurs fois sur cette icône; cela change la disposition des jetons à chaque fois.
Enfin,le mode aléatoire ou les dix positions sont choisies au hasard. On peut cliquer plusieurs fois sur cette icône; cela change la disposition des jetons à chaque fois.
Lorsque l’on utilise deux barres de dominos, seule la barre du haut est affectée par le changement de mode. La barre du bas reste en mode standard.
Positions organisées ou aléatoires
En utilisant les positions des jetons dans le mode standard, les élèves finiront par identifier les nombres par le positionnement des jetons du domino, qui est toujours le même pour un nombre donné. C’est normal et c’est un des intérêts du domino informatisé. A chaque dépôt ou retrait d’un jeton, les autres se réorganisent pour former les figures classiques des dominos en numération décimale. Au final, le fait de reconnaître une figure améliore le comptage car elle facilite le surcomptage. Le surcomptage, c’est l’action de compter en commençant l’énumération par un nombre connu supérieur à 1.
Normalement, pour 1, 2, 3 et quelquefois 4 jetons, le cerveau devrait être capable de concevoir le nombre sans avoir à compter. Ici la position des jetons dans le domino n’a pas d’importance. Mais à partir de 4, l’organisation devient utile pour surcompter. Cette capacité du cerveau humain de reconnaître les petites quantités s’appelle le « subitizing« . Attention : cela ne dispense pas de l’apprentissage du comptage par itération de l’unité à partir de 1. Ce n’est pas parce que l’enfant reconnaît la quantité « 3 » qu’il sait compter et qu’il a acquis la notion de nombre.
Compter ainsi et associer une disposition à un nombre permet à l’enfant d’acquérir la conviction que la disposition résume le comptage du tout; il n’est plus nécessaire de compter à partir de l’unité.

Comptage et changement de position des jetons
Cette activité est plus intéressante à partir des nombres 4 ou 5, puisque les nombres jusqu’à 3 sont reconnus sans comptage. Mais bien sûr, rien n’interdit de la pratiquer sur des nombres plus petits.
Paramétrage : travail libre, « unité », deux barres et mode standard (1,1,2,-).
Démarrer l’activité de comptage comme décrite précédemment sur la barre du haut. S’arrêter lorsqu’on a atteint un nombre-cible, par exemple le 5. Là, changer le mode standard pour le mode « colonnes » ou le mode « aléatoire ». La disposition des jetons change et reflète le nouveau mode (première flèche de l’illustration ci-dessous).
La question à poser est : « est-ce qu’il y en a toujours 5 ? » Les élèves peuvent être tentés de dénombrer sans bouger les pièces, en les pointant du doigt; mais pour éviter le comptage-numérotage, on peut reprendre chaque jeton un à un et le déplacer dans le domino du bas, en reprenant la comptine « et encore 1… » (deuxième flèche). Le domino du bas n’est pas affecté par le changement de mode et affiche donc le nombre 5 sous une forme plus classique et reconnaissable – celle que nous avions au départ du jeu.
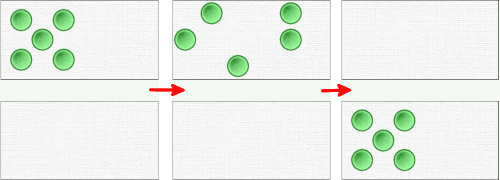
Remarque : il n’y a pas de réorganisation automatique des jetons en mode aléatoire, lorsque l’on en ajoute ou en retire.
Après ces manipulations magistrales, on peut laisser les élèves explorer eux-mêmes. Le comptage est sans doute plus intéressant à pratiquer à deux.
Le nombre 5
Ce qui est abordé ici fonctionne mieux en représentation classique – mode standard.
Sur le sélecteur, on voit une pile de 5 pièces, que l’on peut déplacer en une seule fois vers le domino-unités. La pile se transforme alors en 5 jetons indépendants. La petite animation qui se produit montre les 5 jetons quitter la pile et se déplacer vers leurs positions, ce qui permet de bien comprendre la situation.
Attention, s’il n’y a plus de place pour ajouter 5 jetons, toute la pile rejoint le petit carré à droite du domino. Cet emplacement est une « salle d’attente ». Si l’on veut placer le tas, il faut d’abord retirer du domino les jetons en trop. Donc, mieux vaut commencer sur un domino vide.
La pile de 5 permet de compter à partir de là ! Outre le fait que cela va beaucoup plus vite, l’intérêt est surtout de casser la comptine qui démarre à 1; les élèves comprennent que le 5 est un autre point de départ possible. « J’en mets 5. Et encore 1, 6. ». Lorsque l’élève dit: « j’en mets 5 », il prend la pile de 5 et la place dans le domino. Un seul geste, mais 5 jetons. Ce faisant, on diminue encore l’importance du comptage-numérotage et on précise la notion de nombre comme mesure d’une quantité.
Avec 5 cette activité a un autre intérêt : préparer en douceur les décompositions de base à partir de là : 6=5+1, 7=5+2, etc.
Le comptage à rebours
Le comptage à rebours commence à partir d’un nombre initial de jetons. Ici, la pile de 5 est intéressante car elle permet de démarrer le jeu à partir d’un domino vide sans avoir à compter les unités. Pour ôter un jeton, il suffit de le déplacer dans la zone en-dehors du domino. Le jeton est alors instantanément détruit, les jetons restants se reconfigurent.
Si vous vous lancez dans l’activité, il vaut mieux attendre que les élèves identifient oralement un nombre grâce à la disposition des jetons. C’est pourquoi ici le mode classique me semble nécessaire, au moins au début.
Cette fois la comptine devient: « J’en mets 5 », « J’en enlève 1, 4′, et ainsi de suite. Le fait que les élèves reconnaissent la disposition classique des jetons peut les aider dans cette tâche. S’ils ne connaissent pas la suite numérique, ils pourraient avoir tendance à recompter les jetons restants à partir de 1. D’où l’intérêt de reconnaître une disposition et de l’associer à un nombre. À mon avis, s’ils recomptent, il vaut mieux remettre l’activité à plus tard et les entraîner au comptage incrémental en mode standard.
Pour les élèves qui réussissent très bien le comptage à rebours en mode standard, il peut être intéressant de refaire le jeu en mode aléatoire. Là, il n’y a plus de reconnaissance du nombre par la disposition des jetons ! La mémoire de la suite numérique est mobilisée, avec peut-être un peu de recomptage que l’on voudra bien tolérer ici, en cas d’hésitation – éventuellement mettre deux dominos unités pour faciliter le comptage (paramétrage 1,1,2,-).
Bien sûr cette activité est à moduler selon l’âge des élèves et leurs capacités. D’autres activités faisant intervenir un ou deux dominos unités sont possibles; à chacun d’adapter cet outil à sa classe.
Le nombre 10
Si l’on travaille avec un seul domino, le nombre 10 ne peut pas être dépassé.
La pile de 10, dans le sélecteur, permet de placer 10 jetons d’un seul coup, à condition que le domino soit vide.
L’utilisation de la pile est utile lorsqu’il s’agit de compter à rebours à partir de là. Mais elle permet aussi, avec la pile de 5, de créer rapidement certains nombres.
Placer des quantités de jetons
On fixe un nombre-cible, on recense différentes manières d’y parvenir, et on essaye de déterminer celle qui est le plus efficace (c’est à dire la plus économe en déplacements de pions).
La procédure classique, abordée depuis le début, consiste à placer un à un les jetons jusqu’à l’obtention du nombre-cible. Si le nombre-cible est supérieur à 5, l’élève entraîné va surcompter, grâce à la pile de 5. Pour obtenir 9 jetons, la procédure la plus efficace connue pour le moment est donc de placer la pile de 5 jetons et d’effectuer le comptage itératif jusqu’à 9. Soit 5 manipulations.
Mais nous savons bien que pour placer 9 jetons, il est plus efficace d’en mettre 10 et d’en ôter 1 ! Idem pour obtenir 4 à partir de la pile de 5.
Cette activité est particulièrement riche pour l’apprentissage, car nous renforçons la notion de nombre en cherchant le moyen le plus rapide de l’obtenir. De plus, mine de rien, nous abordons (sans la nommer) la soustraction.
Et la lecture du nombre ?
Comme vous le constatez, en mode travail libre, le nombre est uniquement affiché sous la forme de dominos. Les chiffres ne sont pas affichés. C’est volontaire. Il s’agit ici de se concentrer sur un apprentissage manuel, visuel (par la disposition des jetons) et oral (comptine numérique). L’accompagnement de l’adulte est donc nécessaire, au départ du moins. La lecture des chiffres et nombres n’est pas abordée ici. Aux enseignants de compléter, le cas échéant. Les exercices de construction proposés dans les autres menus ne sont utilisables que si l’élève sait lire au moins les dix premiers nombres.
Autres activités sur le site

Les réglettes Cuisenaire
Pour le dénombrement et la décomposition des nombres.
 Le schéma en barres avec des cases
Le schéma en barres avec des cases
Pour la décomposition des nombres.
 La pesée virtuelle
La pesée virtuelle
Avec des fruits légers, dans le mode « comparer avec des masses virtuelles », pour compter le nombre de triangles.
 La numération avec des billes
La numération avec des billes
En travail libre, poser des billes de différentes couleurs sur les lignes, compter des billes ou des collections de mêmes couleurs.

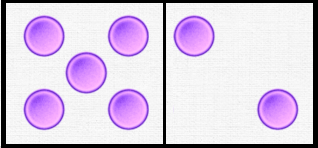 L’aspect cardinal
L’aspect cardinal Lien vers l’activité.
Lien vers l’activité.