Les exemples présentés dans cet article portent sur des barres de trois dominos, qui utilisent des nombres plus grands que 100, ce qui nous permet de comprendre les passages de retenues.

On peut bien sûr utiliser moins de dominos pour travailler les additions. Si S est la somme des termes a et b:

• S <= 10 : deux barres de dominos-unités suffisent (il n’y a pas de retenue donc l’intérêt est surtout de passer du comptage au calcul)
• S<=100 : deux barres de dominos-dizaines+unités suffisent
• S<=1000: prendre trois barres de dominos centaines-dizaines-unités

Nous ne reviendrons pas sur la  technique du passage de la dizaine ou de la centaine avec les dominos. Voyez à ce sujet l’article sur le passage.

L’addition

L’addition est commutative: a + b = b + a = S. Mais cela ne signifie pas qu’il n’y a pas d’ordre dans l’opération. Il y a bien un ordre – nous avons un premier élément a et un second b, mais cet ordre n’a pas d’importance puisque l’opération est commutative.

Mais comme nous avons deux éléments ordonnés, nous mettrons a dans la première barre et b dans la seconde.

À réaliser le calcul suivant : 347 + 264

Nous allons donc poser a dans la barre du haut et b dans la barre du bas :

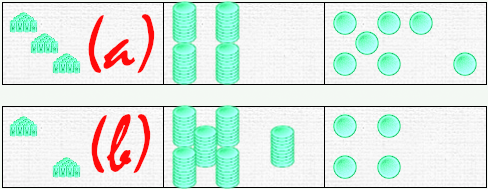
Pour réaliser le calcul, il suffit à priori de déverser le contenu d’une barre dans une autre et de réarranger les pions pour faire disparaître les éventuelles dizaines. On lira le résultat dans la barre restante.

Mathématiquement c’est tout à fait exact. Mais il y a néanmoins un sens à cette opération d’ajout. Dans les dominos, les deux contenus initiaux, les cardinaux a et b, sont détruits dans l’opération, et a est remplacé par S, la somme.  Si nous voulions attribuer un type Vergnaud à l’opération, on dira que c’est une opération de transformation. Or, dans une transformation, il y a toujours un sens.

Dans la vie courante, lorsque l’on fait une addition-transformation, c’est le deuxième élément que l’on ajoute au premier. Dans une recette, quand on demande d’ajouter une pincée de sel, vous la versez dans la casserole qui contient déjà le reste de la préparation. Pas l’inverse. Même si l’opération est commutative.

Donc, nous allons vider la deuxième barre dans la première, et non l’inverse, car nous souhaitons garder le sens de l’opération. Le résultat se lira donc dans la barre qui contient pour le moment la valeur a.

 

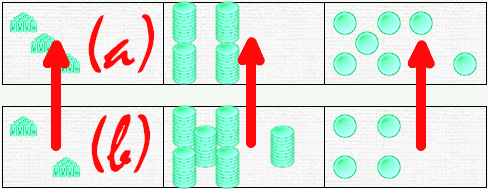
Interrogeons-nous maintenant sur l’ordre hiérarchique des unités. Disons-le tout de go : avec les dominos il n’y a aucune obligation d’utiliser l’ordre hiérarchique traditionnel, à savoir, d’abord traiter les unités, puis les dizaines, puis les centaines. Essayez. Vous verrez que vous pouvez très bien commencer par ce que vous voulez, traiter les éléments comme bon vous semble, et même opter pour le désordre le plus total. Vous devez respecter ces deux seules règles: déverser une barre dans l’autre et effectuer les passages des dizaines, comme indiqué dans les articles sur le comptage.

On ne peut pas faire plus simple. Malgré cela, le domino peut devenir une excellente illustration des additions posées. Je suggère de laisser les élèves s’entraîner comme bon leur semble, afin de les laisser se familiariser. Attention à bien viser, le seul ennui est la disparition d’un pion lorsqu’il atterrit à côté d’un domino.

Ceci nous démontre aussi que les opérations posées, telles que nous avons l’habitude de les résoudre, ne sont rien d’autre que des techniques conventionnelles, et qu’en fait on peut très bien en changer. Vous voulez la preuve ? Voici une opération posée selon une autre technique. Ici, on pourrait commencer à gauche, à droite ou au milieu, l’opération serait toujours la même.

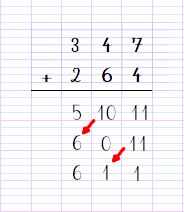
Nous avons indiqué par des flèches les passages de la dizaine. Notez que cette opération n’est pas réalisable avec nos dominos, car 11 ne peut figurer dans le dominos-unités.

Évidemment, l’opération d’addition posée “classique” est enseignée parce qu’elle a un avantage sur les autres techniques : elle est plus concise. Avec deux opérandes elle tient sur 4 lignes -il y a une ligne pour la réponse et une autre qui contient les retenues.

Vers l’addition posée avec le domino

L’opération posée est surtout utile pour des nombres plus grands que 10. Pour le reste, le calcul en ligne et le calcul mental suffisent. L’usage du domino permet surtout d’illustrer la technique opératoire classique avec le passage de la retenue.

Pour commencer donc, soyons explicites et exposons l’objectif à nos élèves: on va apprendre à poser une addition, sur le papier.

On va donc écrire l’addition en colonnes, en respectant bien la consigne de mettre un chiffre par case et de bien aligner les nombres, et on prépare le domino :

 

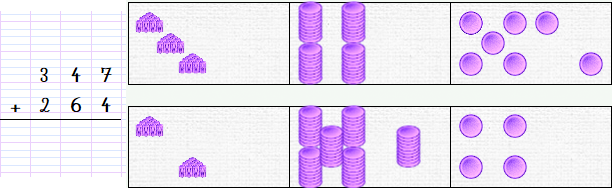
Cette fois, il s’agit de respecter la technique opératoire. Nous allons respecter l’ordre hiérarchique unités, dizaines,  centaines. On commence donc par déplacer les unités, mais sur le domino, cela coince déjà. On peut placer jusqu’à 10 unités, mais il en reste une dans la partie b.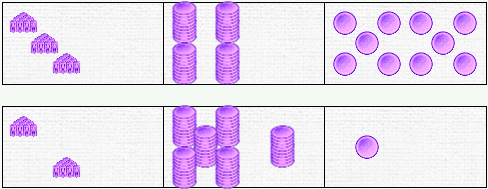S’ils ont déjà un peu d’entraînement, les élèves savent déjà ce qu’il faut faire : le passage ! Et hop, une dizaine de plus dans la colonne des dizaines. On déplace encore le jeton restant de la ligne b vers la ligne a :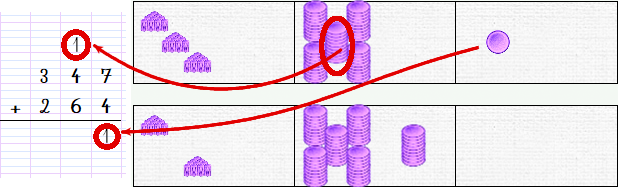

On met bien en parallèle l’unité  et la dizaine supplémentaire dans les dominos de la barre du haut avec l’opération (pour éviter les confusions entre le 1 de la dizaine et le 1 des unités, on aurait pu additionner 265).

On recommence avec les dizaines. Maintenant nous sommes coincés sur les dix dizaines.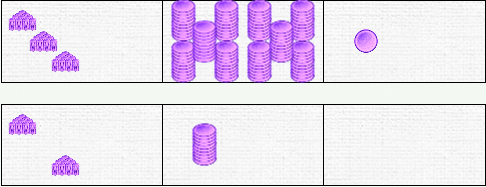

Un passage et nous migrons la dernière pile vers la dizaine du haut, puis notons la correspondance sur notre opération posée :

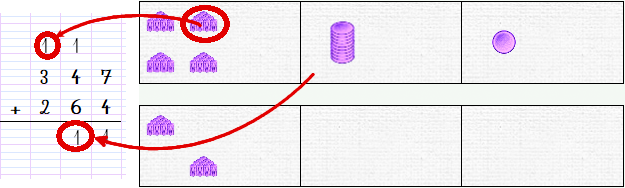
Enfin, il faut encore déplacer les deux centaines restantes, et nous avons la solution :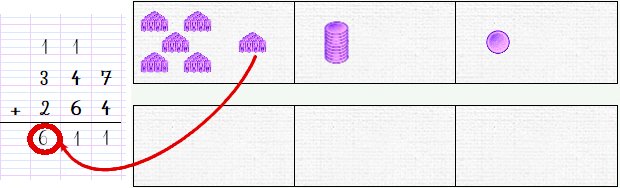

Il est important de bien différencier la ligne des retenues et la ligne du résultat: sur la ligne des retenues, on indique le nombre de dizaines ou centaines qui sont passés (soit toujours 1 s’il y a deux opérandes) alors que sur la ligne du bas, le résultat reflète le contenu du domino.

Intérêt de la manipulation ?

Tout simplement de montrer que la retenue ne sort pas du chapeau. Elle n’a rien de magique : c’est le résultat du passage, la transformation des unités de la hiérarchie inférieure vers la hiérarchie supérieure.

Ceci posé, il faut maintenant revenir à notre opération. Nous n’avons pas encore terminé; de fait, comme nous avons utilisé les dominos, nous nous sommes contentés de lire et d’interpréter le résultat. Mais nous n’avons effectué aucun calcul. Cette fois, on quitte un peu nos dominos et on refait la même opération, mais en calculant.

Entraînement

Dans un premier temps on peut proposer quelques opérations à poser correctement sur le papier, en respectant l’alignement et la position de la retenue, opérations que l’on résoudra avec l’aide des dominos. Petit à petit, bien sûr, on abandonnera les dominos.

Enfin, on abordera les additions posées avec plus de deux opérandes, et ceci nécessairement sans les dominos.