Prochainement sur Actilud.

Vous adorez les énigmes de type « Pixel Art » ? Dans cet article, nous aborderons une technique de calcul intéressante, puis nous présenterons quelques outils du site qui améliorent le confort de jeu.

Le jeu de Pixel Art se trouve dans la section jeux de logique. Il y a deux entrées possibles: l’éditeur, qui permet de créer soi-même un jeu de Pixel art, et le jeu qui permet d’y jouer. Cet article concerne uniquement le jeu de Pixel art.

Au démarrage, les paramètres sont programmés pour fournir une aide optimale avec un jeu de niveau 1, donc facile. Utilisez-le pour vous initier.

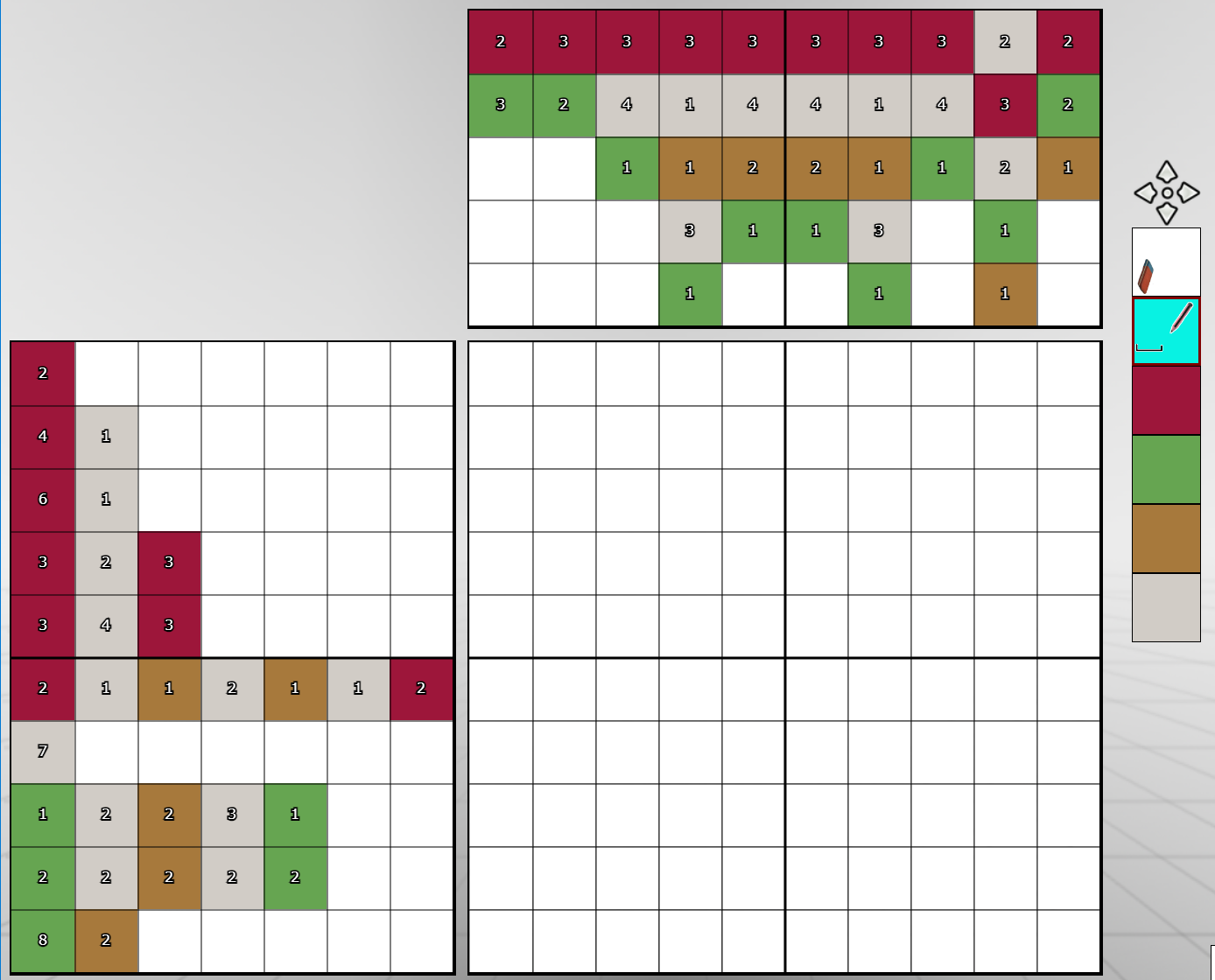
Objectif

L’objectif est de compléter la grille à l’aide du codage dans les deux panneaux latéraux. Voyez la palette de 6 couleurs à droite; il s’agit de colorier toutes les cases à l’aide des couleurs indiquées, à l’exception de la première. Au début, toutes les cases sont dans la première couleur, celle marquée par une gomme. C’est la couleur attribuée aux cases « vides », c’est à dire celles que l’on n’a pas encore traitées. À la fin du jeu, aucune case de la grille ne doit contenir cette couleur.

Dans cette énigme, la couleur de la gomme est le blanc; mais la couleur peut varier en fonction de l’énigme proposée. En général, c’est une couleur neutre, éloignée des autres couleurs.

La seconde couleur, ici le bleu ciel, est celle de l’espacement entre les cases. Elle ne figure jamais dans les panneaux latéraux. Cette couleur peut séparer deux plages de couleur – d’où le symbole d’espacement qui y figure.

Les quatre autres couleurs font partie du codage : chaque case du code, sur les panneaux latéraux, contient un nombre et une couleur : le nombre indique la taille de la plage de cases contigües qui doivent être colorées, et la couleur précise la teinte qu’il faut utiliser.

Ainsi, si on observe la dernière ligne, on voit qu’il y a 8 cases contigües de couleur verte et deux cases de couleur marron. Il y a donc 10 cases de couleur. Or, comme notre grille contient exactement 10 cases, nous pouvons remplir la dernière ligne entièrement, sans utiliser la couleur d’espacement.

Remarquez le petit point vert sur le 8 et le 2 : c’est le résultat de l’aide automatique que nous avons laissée active. Elle nous indique que les deux plages ont été placées. Nous y reviendrons.

Dans les cas où le total ne fait pas 10, il faut compléter les intervalles entre les plages par des espaces, en utilisant la couleur d’espacement.

Toute la problématique est de savoir où placer ces espaces !

Il y a d’autres rangées que l’on peut compléter entièrement – je vous laisse les découvrir.

La formule pour y arriver facilement

Dans une rangée, pour trouver les cases à colorier dès lors qu’il y a des espaces, on doit rechercher les cases constantes dans toutes les répartitions possibles entre plages de couleur et espaces. C’est un travail fastidieux. Cette technique est utilisée par l’ordinateur, car elle repose sur la rapidité de calcul de la machine. Pour un humain c’est faisable… dans une autre échelle de temps. Mais heureusement il existe une technique plus sophistiquée.

Ce que fait la machine…

Néanmoins, pour bien comprendre notre formule de calcul, voyons ce que fait l’algorithme très simple du jeu. Dans la grille montrée en début de cet article, extrayons la ligne marquée « 3,2,3 » :

Nous allons la traiter à la façon d’une machine. Pour cela, voyons toutes les répartitions possibles des plages de couleur (rouge, gris, rouge) et des espaces (en bleu). Il y en a 10 en tout :

On constate que deux cases – la troisième et la huitième- sont constantes dans toutes les répartitions. On peut donc les placer dans la grille avec certitude :

On peut obtenir le même résultat en analysant plus finement la situation, grâce à un calcul assez simple : celui de l’intervalle d’incertitude. La procédure prend trois étapes :

• calculer l’étendue des plages
• déterminer l’intervalle d’incertitude
• colorier !

 Calcul de l’étendue des plages

L’étendue des plages est la taille minimum que la somme des plages doit atteindre, en comptant les espaces s’il y en a.

Le calcul est facile: on additionne toutes les tailles indiquées dans la rangée. Par exemple, pour la ligne contenant 3, 2, 3 l’étendue sera 3+2+3=8.

À cela on ajoute 1 chaque fois que deux cases de même couleur sont contigües. Cela n’arrive pas dans notre exemple. Mais il faut être très attentif sur ce point. Pourquoi faut-il ajouter 1 ? Parce que si deux plages de même couleur sont côte à côte dans l’énigme, c’est qu’elles sont forcément séparées par au moins 1 espace dans la grille. Sinon dans l’énigme il n’y aurait qu’une seule plage, plus longue. Comme notre étendue est une taille minimum, nous ajoutons donc la plus petite quantité d’espace possible : 1.

Attention : on compte le nombre de contiguïtés, pas le nombre de cases !

Voici un exemple de codage, tiré du jeu « Le roi ».

L’étendue ici est : 1+1+1+1+1+1+2+1+3+1=13 à laquelle on ajoute 2 (1 pour les deux plages marron foncé côte à côte et 1 pour les deux plages marron clair côte à côte), soit un total de 15.

Dans les jeux de type silhouette, l’addition des contiguïtés est systématique car il n’y a que 2 couleurs -l’espace en blanc et la couleur noire. Le nombre de contiguïtés est le nombre de plages dans notre énigme diminué de 1.

Observez l’exemple ci-dessous, tiré du jeu prise de poids :

Ici l’étendue est 1+1+2+1+1=6 auquel on ajoute 4, soit un total de 10. En effet, il y a 4 contiguïtés (5 plages -1).

Comme notre grille a 10 cases, on peut placer sans se tromper les plages et les espaces car il n’y a qu’une seule solution :

Voici la méthode pour faire les calculs. On compte à partir de la gauche ou de la droite, selon l’emplacement le plus facile, et on additionne mentalement la valeur de la plage à chaque saut de case. Puis on revient en arrière en ajoutant 1 par saut de case lorsqu’elles sont contigües, ce qui est toujours le cas dans les énigmes « silhouette ».

Cette illustration explique le cheminement de calcul. Les flèches bleues indiquent le sens des additions; les rouges indiquent le sens des incrémentations à chaque contiguïté.

Si l’étendue est égale à la taille de la rangée, on peut compléter immédiatement. Mais que faire lorsque l’étendue est inférieure ? Eh bien là, on calcule l’intervalle d’incertitude.

Calcul de l’intervalle d’incertitude

Facile :

intervalle d’incertitude = taille de la rangée – étendue

Dans l’exemple le roi ci-dessus, l’étendue de notre rangée est de 15 et la rangée mesure 35 cases. L’intervalle d’incertitude est donc de 35-15=20.

Colorier les cases

La règle : tout ce qui dépasse l’intervalle d’incertitude peut être colorié.

Commençons tout de suite par un cas extrait de l’énigme tir au but.

Ici l’étendue est de 8 (3+4+1 contiguïté) et l’intervalle vaut 2 (10-8). Tout ce qui dépasse la longueur de 2 peut être affiché.

Pour placer les cases coloriées, on compte les cases à partir de 1 chaque fois qu’une nouvelle plage démarre. Si le comptage dépasse l’intervalle d’incertitude, on colorie la case dans la couleur de la plage. Une fois qu’on a atteint la longueur de la plage, on regarde si la plage suivante est de la même couleur. Si c’est le cas, on saute un espace (sans coloriage, puisque nous sommes sous l’intervalle). Puis on recommence avec la plage suivante.

L’illustration ci-dessous indique bien la procédure mentale à suivre. Comme vous le voyez: c’est du comptage. Dès que je dépasse 2, la valeur de l’intervalle, hop ! je colorie.

Le trait d’union sur l’illustration symbolise l’espace.

Revenons à l’énigme de la petite maison.

L’étendue est de 8 (3+2+3) et donc l’intervalle de 2 (10-8).

On obtient ceci : la case 3 et la case 8 de la ligne sont en rouge. Et vous voyez que le résultat est le même que notre algorithme précédent, mais obtenu de manière plus « humaine ».

Application de la technique à une partie de la rangée

Bien sûr, au fur et à mesure du jeu, des cases vont se remplir. Les cases près des bords sont d’ailleurs les plus intéressantes. Il peut donc arriver, au cours du jeu, que vous avez placé avec certitude certaines plages mais qu’il en reste d’autres à placer dans la rangée. Dans ce cas, ne comptez que ce qui se trouve à l’intérieur du nouvel espace et, pour calculer l’intervalle d’incertitude, ne prenez pas la taille de toute la rangée mais uniquement celle de la zone à étudier à laquelle vous soustrayez l’étendue des plages qui s’y trouvent.

Complément : les bords

Les bords, justement, sont une approche intéressante. Examinez-les toujours car si vous pouvez placer des cases aux bords, vous pouvez valider les rangées qui touchent ces bords. Un exemple est le jeu le roi, où la ligne du bas peut être résolue facilement.

Une fois que cette ligne du bas est posée, certaines plages en bas des colonnes peuvent être complétées, celles dont nous avons placé la dernière case. Mais je vous laisse le découvrir.

Quelques outils

La pipette

La pipette permet de changer une couleur. Elle est proposée au cas où vous auriez du mal à discerner certaines teintes. Dans ce cas n’hésitez pas à vous en servir.

Cliquer sur la pipette, cliquer sur une couleur, choisir le réglage, cliquer à nouveau sur la pipette pour quitter le mode pipette.

Défaire / refaire

Les deux icônes classiques pour changer d’avis… et changer d’avis lorsqu’on a changé d’avis. Attention, la mémoire est limitée, elle ne porte que sur quelques coups. L’outil concerne les coups joués, pas les changements de couleurs ou l’effacement complet de la grille.

 

La calculatrice

L’idéal étant de s’en passer, on va beaucoup plus vite avec du calcul mental. Ce jeu est d’ailleurs un excellent entraînement.

La gomme

Permet d’effacer complètement la grille pour recommencer sur une grille vide. Annule aussi la liste des actions à défaire/refaire.

Enregistrer, charger

Permet d’enregistrer le jeu en cours dans le dossier de téléchargements, et de le récupérer plus tard pour y jouer.

Le feu tricolore barré

Permet d’arrêter les scintillements lorsqu’il y a des erreurs.

Les réglettes de guidage

Les réglettes apparaissent lors d’un clic dans un panneau. On peut les déplacer en cliquant ailleurs, en utilisant les touches fléchées du clavier ou la molette de la souris. Pour les faire disparaître, cliquer dans le coin vide en haut à gauche, entre les panneaux.

Les réglettes sont surtout pratiques sur les grandes grilles, où il devient difficile de suivre une ligne ou une colonne sur toute la longueur.

Pour colorer une ou plusieurs cases

Pour choisir la couleur, Il y a deux méthodes.

• cliquer sur une des couleurs de la palette – elle est prévue pour cela ! Le curseur en forme de crayon indique la couleur en cours.
• quand on hésite sur une teinte, on peut aussi cliquer dans un des panneaux sur la plage que l’on compte renseigner dans la grille. La couleur de la case cliquée est alors sélectionnée et la palette reflète votre choix. Ceci fait aussi apparaître une réglette.

Pour colorier une case, une fois la couleur choisie, il suffit de cliquer dans la case. On peut aussi déplacer le pointeur tout en maintenant enfoncé le bouton de la souris – ou glisser le doigt sur l’écran tactile- ce qui permet de colorer une plage. Dans ce mode, un garde-fou empêche de déraper vers les rangées adjacentes.

L’aide

Il y a deux formes d’aides disponibles :

• l’aide à la volée, qui se produit dès que l’on modifie une case;
• l’aide sur demande, utile lorsque l’on a besoin d’un coup de pouce.

Le paramétrage se fait dans le menu de départ; on peut y retourner à tout moment pour le modifier.

L’aide à la volée

• indiquer les cases erronées : si on colorie une case dans la mauvaise couleur, celle-ci se met à scintiller. Le programme effectue une comparaison directe avec le modèle en mémoire; cette aide permet donc d’éviter les bévues, mais elle facilite aussi la triche;
• cocher les indices (très utile) : coche, dans les panneaux latéraux, les cases dont les plages sont placées dans la grille de manière plausible, même si ces plages ne sont pas, en réalité, à la bonne place. Une case est cochée si elle correspond à une plage complète et si celle-ci est à une position plausible. Cette aide est vraiment intéressante et je la conseille : en effet, cocher automatiquement les plages plausibles simplifie la lecture des énigmes, sans pour autant donner d’indication sur le modèle sous-jacent. Lorsque l’on joue dans une revue, avec crayon et gomme, c’est ce que l’on fait soi-même, en général.

L’aide à la demande

• trouver les erreurs: fonctionne comme l’aide à la volée, mais porte sur toute la grille. Trouve les cases erronées par comparaison avec le modèle. Permet d’éviter les bévues, lorsque l’on soupçonne une incohérence.
• trouver les erreurs et montrer les rangées intéressantes :
  • si une erreur est détectée, on se retrouve dans le cas précédent.
  • s’il n’y a pas d’erreur, une rangée intéressante est désignée par une réglette. Le conseiller affiche le nombre de cases à colorier dans la rangée, ou indique s’il est possible de compléter toute la rangée.

Si possible, avancez toujours le plus loin possible, d’abord à partir des bords, puis à partir des autres rangées que vous avez déjà complétées. Sur les grandes grilles, le solveur peut mettre plusieurs secondes avant de trouver la rangée la plus intéressante, car il compare toutes les combinaisons sur toutes les rangées avant de faire son choix.

Le niveau des grilles

N’hésitez pas à sauvegarder un jeu pour le reprendre plus tard. La concentration demandée pour résoudre les grilles complexes est intense ! Pour vous donner une idée de la difficulté, le niveau des jeux indiqué dans le menu est en réalité, le nombre de passes effectuées par l’algorithme, lorsqu’il teste une grille. Sachant qu’une passe est une boucle complète sur toutes les indications des deux panneaux, et que la grille Coco a nécessité 19 passes, il y a donc eu 1330 évaluations. Bien sûr, vous n’en ferez pas autant, -enfin j’espère- car nous autres humains sommes capables de discerner sans calcul les lignes et les colonnes les plus utiles. N’hésitez pas à utiliser l’aide à la demande, surtout lorsque vous êtes bloqué. Elle rend le jeu plus plaisant, sans pour autant tout révéler.