Article mis à jour, publié initialement le 13 janvier 2022 sur Tice67

Dans cet article, je vais proposer des pistes de travail sur le modèle en barre à partir du site Actilud.com qui, une fois adaptées à votre classe, vous feront gagner du temps et de l’efficacité grâce au numérique.

Cet article n’a pas pour but d’expliquer dans les détails l’intérêt pédagogique des schémas en barre; il existe pour cela toute une littérature.

Le schéma en barre additif

Actilud.com, numération et problèmes de base, B1: initiation au schéma.

Prenez le temps d’observer les différentes configurations possibles des paramètres. Celle que nous allons utiliser dans cet article est 4-1-3.
Cette configuration permet une présentation à toute la classe, sur TBI ou vidéo-projecteur, ainsi que le travail individuel sur un problème proposé par l’enseignant. Variez le total ou l’affichage en fonction du niveau de classe et des difficultés des élèves.

Avec ces paramètres on obtient ceci :

Vous pouvez déplacer le point d’interrogation sur n’importe laquelle des trois barres :

Le schéma en barre sur Actilud est adaptable; si vous travaillez le comptage avec la dizaine voici le paramétrage 4-2-1 :

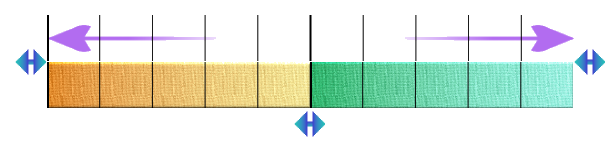
Une démarche pour initier les élèves

La démarche traditionnelle (sans le numérique) consiste à amener progressivement les élèves à l’élaboration d’un schéma en barre, à partir de matériel comme des cubes ou des réglettes. Comme vous vous en doutez, avec cette méthode « artisanale », il faut procéder par étapes et l’intervention de l’enseignant est indispensable, à plusieurs reprises, pour enfin arriver à un schéma viable.

Grâce au numérique, nous pouvons inverser la démarche et aller beaucoup plus vite. Le schéma sur Actilud n’est pas une abstraction mais c’est une « machine virtuelle » tout à fait opérationnelle qui fonctionne comme une calculatrice !

L’idéal est d’utiliser un TBI. Si vous n’en avez pas, prenez un vidéoprojecteur. Une connexion Internet est nécessaire aussi, bien entendu. Si vous avez une classe mobile d’ordinateurs ou de tablettes, c’est le moment de les distribuer pour permettre aux élèves d’expérimenter le modèle, seuls ou en petits groupes.

La démarche proposée ci-dessous n’est évidemment pas normative: l’enseignant doit l’adapter en fonction de la classe et de la progression. Cependant, il faut être suffisamment à l’aise avec sa classe et avec le numérique, pour laisser de la liberté aux élèves. Soyez prêt à faire face à un peu d’imprévu ! Si vous voulez tout contrôler jusqu’au moindre clic, ça ne marchera pas !

Première étape: découverte du modèle – activité de recherche

Présentez le modèle avec le paramétrage indiqué plus haut. Voici le questionnement :

C’est « une machine à résoudre les problèmes ». Trouvez comment elle marche. Pourquoi peut-on dire que c’est une machine à résoudre les problèmes ? Quelles sortes de problèmes peut-elle résoudre ?

Dans un premier temps, demandez à vos élèves de ne pas utiliser le point d’interrogation. Laissez les chercher sur leur écran, et/ou imaginer des réponses et les présenter sur le TBI.

Les élèves percevront très bien l’intérêt de la machine, surtout s’ils ont l’habitude de collaborer – sinon c’est le moment de le leur apprendre.

Au CP nous avons vu des élèves « pousser » le modèle dans ses limites, ce qui leur fait aborder le rôle du zéro :

C’est quoi ? Mais c’est 0=0+0. Le zéro n’est pas affiché car il n’y a plus de place pour l’écrire. C’est normal : si j’ai zéro bille, je n’ai « rien ».

Les réponses attendues

Sans vouloir préjuger des réponses de vos élèves, il y a fort à parier que celles-ci tournent autour du calcul. C’est une machine à résoudre des problèmes car elle permet de faire des calculs, en particulier l’addition (et la soustraction s’ils la connaissent déjà).

Deuxième étape : calculs et problématisation

Cette démarche s’effectuera sans doute sur plusieurs séances.

Notre objectif n’est pas de faire du calcul, mais bien de résoudre des problèmes. Pour cela, nous inversons les procédures habituelles – nous allons partir du calcul pour trouver un problème.

La phase de calculs

C’est le moment d’aborder l’addition (barre du haut), puis la soustraction avec les barres du bas.

Comment procéder – l’addition

On commence par l’addition, on crée un problème. Puis on procèdera de même avec la soustraction.

Pour commencer l’enseignant positionne le point d’interrogation sur une des barres – commencer donc par la barre du haut pour l’addition, puis modifier les tailles des barres et demander aux élèves de trouver la valeur (longueur) de la barre cachée.

La question est :

Quel est le calcul ?

Si les élèves peuvent utiliser leur tablette, ils trouveront assez facilement la valeur réponse en reproduisant le modèle. Mais ici, l’important n’est pas de trouver la valeur de la réponse, mais le calcul qui mène à cette valeur, et que le modèle n’indique pas :

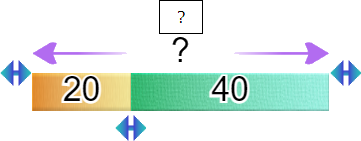
Réponse que l’on peut schématiser ainsi (le cas échéant, si votre classe s’y prête, on peut aborder de suite les deux écritures possibles de notre équation- mais s’il y a le moindre risque de confusion ne prenez qu’une seule des deux écritures) :

? = 20 + 40

20 + 40 = ?

La problématisation

Sur le même type d’opération de calcul, il ne faut pas perdre trop de temps et  rapidement problématiser. Pour cela, on peut poser la question suivante aux élèves :

Quel problème peut-on inventer avec ce calcul ?

Dans le cas de notre opération, la réponse attendue est un problème simple de type Vergnaud, tel qu’on peut en trouver sur le site :

Alice a 20 billes. Elle joue contre Bob et en gagne 40. Combien de billes a-t-elle maintenant ?

Avec des billes, il est probable que les élèves inventent un problème de transformation. Bien sûr, tous les types de problèmes sont aussi les bienvenus ! Voici un autre exemple de proposition, faisant intervenir une composition, toujours avec des billes :

Alice a 20 billes, Bob en a 40. Combien de billes ont-ils en tout ?

En procédant ainsi, l’enseignant peut, s’il le désire, discuter de la pertinence de chaque énoncé proposé, l’améliorer, puis l’écrire afin de réaliser une première banque d’énoncés créés collectivement, à distribuer ensuite aux élèves.

Une fois que les élèves maîtrisent un énoncé, ils peuvent s’amuser à changer les paramètres et chacun peut inventer son problème, puis demander aux autres de le résoudre.

Comment procéder – la soustraction

Notons au passage qu’une soustraction, dans le cadre de ce schéma, est toujours une addition à trou ! On regarde ce qu’il manque sur une barre pour arriver au total qui figure sur la barre supérieure.

Si les élèves n’ont pas encore abordé la soustraction, on peut en rester au stade de l’addition à trou. S’ils ont déjà abordé la soustraction, c’est le moment de leur faire comprendre qu’une addition à trou est une soustraction.

Dans cette situation, si on part du modèle en barre, la question est: combien dois-je ajouter à 34 pour obtenir 60?

On obtient donc les calculs suivants :

60 =  ? + 34

60 – 34 = ?

Comme auparavant, entraînons nos élèves à trouver les réponses par calcul sur la même situation, en faisant varier les valeurs, puis problématisons.

Ici le type de problème devient :

Alice et Bob ont 60 billes en tout. Bob en a 40. Combien de billes possède Alice ?

La démarche doit être répétée pour la barre de droite. Les élèves remarqueront que certes l’écriture change légèrement (60 = 34+?) mais que c’est exactement la même démarche que pour la barre de gauche.

Troisième étape: résoudre un problème donné

Cette fois, l’enseignant va écrire un énoncé au tableau. Les élèves disposent du schéma sur leur tablette et/ou peuvent reproduire le schéma sur un cahier.

Si les élèves reproduisent le schéma sur le cahier, ils vont avoir des difficultés à conserver la proportionnalité de la taille des barres sur leur dessin, en particulier si les nombres sont grands. Les élèves ont toujours tendance à suivre le modèle qu’on leur présente, et vont perdre du  temps à représenter les barres de la manière la plus précise.

Or, le respect de la taille n’est pas important. Ce qui l’est, en revanche, c’est l’écriture des données aux bons endroits. La taille d’une barre doit figurer sous la forme d’un nombre, peu importe si la proportionnalité n’est pas visuellement respectée. C’est ainsi que nous pouvons augmenter progressivement leur niveau d’abstraction.

Cette fois, l’énoncé proposé par l’enseignant peut être dans l’une ou l’autre des catégories qu’on a vues: avec addition ou soustraction. Aux élèves d’essayer de le résoudre à l’aide du modèle.

Quatrième étape: entraînement sur le site

Actilud.com, numération et problèmes de base, exercice C1: composition d’états avec schéma.

L’intérêt du site est qu’il peut obliger (selon le paramétrage) à placer les étiquettes de données sur les bonnes barres. C’est utile pour travailler la compréhension des problèmes. Le vocabulaire est volontairement assez simple car l’objectif est d’abord de permettre aux élèves de résoudre des problèmes simples, non d’enrichir leur vocabulaire (ce qui pourra être fait plus tard, une fois la maîtrise acquise, en proposant d’autres problèmes sur fiches).

Grâce au site, l’enseignant peut très facilement adapter ses consignes au niveau des élèves :

Dans l’illustration ci-dessus, on utilise le schéma pour calculer automatiquement la réponse. Ici, l’intérêt est de travailler l’énoncé, laissant les calculs à la machine. Où l’on voit à quel point le numérique facilite les choses !

Dans l’illustration ci-dessous par contre, le schéma est utilisé pour comprendre l’énoncé, mais le calcul est laissé à l’élève.

 

Cinquième étape (et suivantes…)

Il est possible d’aborder d’autres types de problèmes additifs (transformation, comparaison, etc.) en s’inspirant des étapes vues précédemment. Progressivement, on peut constituer une banque de problèmes simples constituant une référence pour les élèves.

Traiter des problèmes avec des nombres plus grands ?

Le plus grand nombre possible est 100, avec le schéma en barre sur Actilud. Utiliser le modèle pour des nombres plus grands n’est pas possible, tout simplement pour des raisons d’ergonomie . Mais pour une initiation aux problèmes cela n’est pas gênant. Une fois que les élèves ont compris la démarche avec le site et des nombres inférieurs à 100, ils peuvent reproduire le schéma sur leur cahier avec des nombres bien plus grands.

Voici la vidéo. Si elle ne s’affiche pas, actualisez la page.