Le jeu « Masse et poids à travers le système solaire » permet de comprendre la différence entre masse et poids. Mais c’est aussi une bonne mise en pratique de la notion d’encadrement. À travers la genèse du jeu, cet article détaille les principes mis en œuvre et leurs conséquences. On comprendra enfin pourquoi il est difficile de peser un citron sur Phobos.
Les principes
La masse est une valeur qui mesure la quantité et la qualité de la matière. La masse se mesure en grammes (g). Par exemple, un litre de plomb fondu est plus lourd qu’un litre de verre en fusion.
Une masse exerce une action sur l’espace-temps: la gravité, encore appelée pesanteur. Plus la masse est importante, plus la gravité est forte. Dans l’espace, chaque astre exerce sa propre attraction sur l’environnement et subit celle des autres, en fonction de sa masse et de la distance qui le sépare des autres masses.
Sur Terre, on a des instruments qui permettent de mesurer finement la gravité. Plus on s’élève en ballon, plus la gravité diminue, car on s’éloigne du centre de gravité. Mais si on se place au-dessus d’un important massif rocheux, comme une montagne, elle augmente, car la masse sous le ballon est plus importante.
Le poids est une valeur qui mesure l’action de la gravité sur la masse.
La masse et le poids sont liés par la formule : P = Mg, où P est le poids exprimé en Newtons (N), la masse est exprimée en grammes et g est le coefficient de gravitation, exprimé en m/s² (mètres par seconde au carré).
Les dispositifs grand public qui mesurent le poids sont rarement gradués en newtons. On préfère utiliser le kg ou le g. Dans ce cas, la formule précédente reste valable mais les unités changent. Le poids est exprimé en « gramme », ce qui, pour un physicien, est plutôt une erreur. Aussi, pour faire la différence, on parlera de « gramme-force » ou « gramme-poids ». Le coefficient g n’a plus d’unité et vaut 1, et donc nous avons P=M.
Le pèse-personne et la balance électronique de table que l’on place dans sa cuisine pour mesurer la quantité de farine ou de sucre, sont les objets de mesure du poids les plus usuels. Le fonctionnement de ces objets repose sur un ressort, qui se comprime plus ou moins selon le poids que l’on place sur le plateau. Ces balances sont sensibles aux variations de pesanteur.
Pour mesurer la masse, on utilise une balance Roberval. Pourtant, pour fonctionner, une balance Roberval a besoin, elle aussi, de la pesanteur ! Essayez de la faire fonctionner dans une station spatiale en apesanteur ! Vous aurez quelques soucis pour actionner les plateaux.
Alors pourquoi dit-on que la balance Roberval mesure la masse ?
Comme les plateaux sont rapprochés, on considère que la pesanteur qui s’exerce sur le plateau de gauche est la même que celle qui s’exerce sur le plateau de droite.
Sur Terre, une orange pèse environ 200g. Je place mon orange sur le plateau de gauche et je mets l’équivalent de 200g en masses marquées sur le plateau de droite. J’obtiens un équilibre.
Si je me rends maintenant à la surface du soleil, l’orange ne pèse plus 200g mais 5,6kg-poids ! Mais les masses marquées seront elles aussi plus lourdes, dans la même proportion. Je pose l’orange sur le plateau de gauche : celui-ci descend. Pour rétablir l’équilibre, je pose 200g de masses marquées sur le plateau de droite. Cela revient à poser 5,6kg-poids. On obtient finalement le même équilibre que sur Terre. La mesure sur la balance Roberval ne dépend donc pas de la pesanteur.
Ceci en théorie. Car, en pratique, les choses sont un peu plus compliquées.
La genèse du jeu
Lors de la programmation initiale de la balance Roberval, et plus tard celle de la balance électrique, j’avais intégré la formule P=Mg avec le paramètre g qui indique le rapport entre coefficients de gravité. Ce rapport vaut 1 pour la gravité terrestre. L’idée était de pouvoir créer facilement un jeu où il suffirait de modifier ce paramètre pour simuler un autre astre. Comme la gravité est 28 fois plus élevée sur le Soleil, il suffit de remplacer la valeur 1 par la valeur 28 et le tour est joué.
Mais, lorsque j’ai finalement créé ce jeu, les choses n’ont pas été aussi simples que je le pensais au départ…
La masse des fruits et légumes et la précision
Tout d’abord, il faut savoir que les fruits et légumes ont une masse qui est générée aléatoirement de façon à imiter au mieux la nature. Un citron, dont la masse mesurée est de 113g, peut avoir une masse effective différente. Ici, elle est de 112,84453671587923 g.

Objectivement, le plateau de gauche, plus lourd, devrait pencher vers le bas. Pourquoi cet équilibre ? Observez l’illustration ci-dessus. En bas de la balance figure la mention « 0,5g ». C’est une indication de la précision, qui est de ±0.5g. La différence entre la masse du citron et les celle des masses marquées est dans les limites de la précision : -0.5g < (112,84453671587923 – 113)g < 0,5g et c’est pourquoi les plateaux s’équilibrent.
La précision est une mesure des forces de frottement. Notre balance essaye de respecter au mieux les lois de la nature, et donc les forces de frottements sont simulées, elles aussi. Ici, elles ont été ajustées de façon à permettre l’utilisation de la plus petite masse marquée possible, celle de 1g. Notre balance n’est précise qu’au gramme près.
Dans le jeu des pesées virtuelles, la précision a été diminuée. Elle est de ±5g (plus la précision est petite, plus sa valeur est grande !) :

L’objet le plus léger est le triangle bleu, dont la masse est de 10g. Pour équilibrer les plateaux il faut donc diminuer la précision; elle est au décagramme près. D’ailleurs, dans ce jeu, on ne trouve pas de cerise, car la masse d’une cerise risque d’être trop faible pour contre-balancer les forces de frottement. Si on pose une cerise sur un plateau vide… eh bien, il ne se passe rien.
Rendez-vous sur Phobos
Phobos, un des deux satellites naturels de Mars, est tellement léger qu’il ressemble plutôt à un caillou. La force qu’il exerce sur les corps à portée est trop faible pour qu’il puisse les agréger et ressembler aux autres planètes.

La pesanteur sur Phobos est bien plus faible que sur la Terre. Et c’est là que les ennuis commencent si on veut peser un citron sur Phobos :

Le citron est beaucoup trop léger ! Il faut prendre un fruit bien plus lourd. Le melon, par exemple :
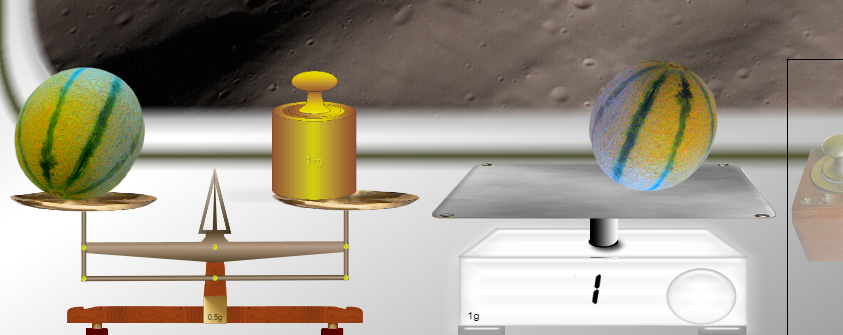
La balance à ressort bouge à peine et mesure un poids de 1g. La balance Roberval, quand à elle, s’équilibre pour toutes les masses comprises entre 430g et 2429g :

Pourquoi ce phénomène ? À cause de la précision de la balance, bien sûr ! Attention, les forces de frottements sont les mêmes, que ce soit sur Phobos ou sur Terre. L’intervalle de précision, exprimé en grammes, ne change pas; mais c’est sa valeur exprimée en g-poids qui est modifiée, à cause de la gravité plus légère. Une masse marquée de 200g ne pèse plus que 0,1g-poids sur Phobos. C’est insuffisant pour actionner les plateaux. Voyez ci-dessous le calcul de l’intervalle des poids limites. Pour Phobos, l’intervalle est de ]-1000g-poids, +1000g-poids[ (les bornes sont ouvertes, c’est à dire que les plateaux vont bouger à partir d’une différence de ±1000g-poids). Tant que la différence de poids entre les deux plateaux est comprise entre ces deux bornes, la balance ne bougera pas. Les plateaux se meuvent dès que l’on atteint ou dépasse une des deux bornes. L’intervalle a donc une étendue de 2000g-poids, à laquelle on retranche 1 à cause des bornes ouvertes, soit 1999g-poids. Cette étendue, nous l’avons mesurée avec les deux pesées ci-dessus : elle représente la valeur absolue de la différence entre les deux pesées que nous avons effectuées : | 2429 – 430 | = 1999.
Remarque : on peut estimer correctement la masse du melon en faisant la moyenne des deux mesures. Mais nous n’allons pas jusque là dans le jeu. Ici elle est de 1429,5 g à ±0.5g près.
En fin de compte, pour Phobos, notre balance n’est pas assez précise. J’ai intérêt à la remplacer par un modèle bien plus précis.
Pour faire ce jeu, J’aurais pu modifier la précision des balances, ce qui, sur Terre (mais pas sur Phobos, bien sûr) aurait exigé des pesées avec le décigramme, le centigramme et le milligramme. Or, il est déjà assez compliqué de peser correctement jusqu’au gramme. Il y a aussi un problème d’ergonomie, celui de la taille des masses marquées de plus en plus légères, et donc visuellement de plus en plus petites, qui doivent néanmoins rester suffisamment grandes pour être saisies avec la souris ou le doigt. J’ai donc abandonné l’idée.
J’aurais pu aussi adapter la précision de la balance en fonction de la pesanteur. Mais ceci aurait induit les joueurs en erreur – l’idée est d’utiliser le même dispositif sur tous les astres et de ne surtout pas le changer entretemps.
Voilà pourquoi ce que je prévoyais être un simple jeu de pesée est finalement devenu un jeu d’encadrement d’un intervalle de pesées. Sur les astres à faible gravité du moins.
Rendez-vous sur le Soleil
Notre astronef est muni d’un champ magnétique suffisamment puissant pour éloigner les particules ! Sinon, il n’aurait pas pu traverser la couronne solaire qui a une température infernale d’un million de degrés, puis résister à la température de surface de 5500°.
Ici la pesanteur est beaucoup plus élevée. Voyons ce qu’il se passe et reprenons notre citron. Sur la balance à ressort, il pèse environ 3200 g-poids.

Passons à la balance Roberval. Là, nous rencontrons une autre surprise : impossible d’équilibrer les plateaux !


Que se passe-t-il ? Là encore, c’est un problème de précision.
Les masses que l’on place sur les plateaux sont 28 fois plus lourdes que sur Terre. Donc, une masse marquée de 1 g va peser 28g-poids sur le Soleil.
Or, notre citron, qui ne pèse pas un nombre précis de grammes, ne peut donc pas être correctement pesé. Soit il est trop lourd, soit trop léger. Tout ce que nous pouvons faire, c’est l’encadrer: 124g < masse citron <125g
Sur le soleil notre balance Roberval est devenue beaucoup trop précise. Pour avoir une meilleure mesure, il faut utiliser des masses marquées plus légères, ou diminuer la précision de la balance !
Et le melon ?
Heureusement, nos balances sont de très bonne qualité. La balance Roberval est une simulation d’un acier très solide. Quand à la balance à ressort, elle est capable d’amortir des objets très lourds, même si on dépasse le seuil maximum toléré, et ceci sans usure. Néanmoins, le melon n’a aucune chance de pouvoir y être pesé :

Calculer l’intervalle des poids limites
Cet intervalle est celui dans lequel une différence de poids entre les plateaux ne produit aucun effet. Le calcul de l’intervalle des poids limites est assez simple. On prend la valeur inférieure et la valeur supérieure de l’intervalle de précision et on la divise par le coefficient de gravité.
L’intervalle de précision par défaut est ]-0,5g, +0,5g[
Voici les différents coefficients de gravité utilisés dans le jeu :
Soleil:28,02
Mercure:0,377
Venus:0,905
Terre:1
Lune:0,1657
Mars:0,379
Phobos:0,0005
Jupiter:2,528
Europe:0,133
Saturne:1,065
Uranus:0,886
Neptune:1,137
Sur Terre : ]-0,5g-poids, +0,5g-poids[ La balance penche dès que la différence entre les deux plateaux est de 0.5g-poids.
Sur Phobos : ]-1000g-poids, +1000g-poids[ La balance penche si la différence entre les deux plateaux est de 1000g-poids au moins. En-dessous, elle ne bougera pas.
Sur le Soleil : ]-17,8 mg-poids, +17,8mg-poids[ Si on pèse un fruit ou un légume, le plateau penche la plupart du temps d’un côté ou de l’autre, car la différence entre les plateaux est le plus souvent hors de l’intervalle indiqué, étant donné que l’on utilise des masses marquées limitées au gramme.
 Lien vers l’activité : masse et poids à travers le système solaire
Lien vers l’activité : masse et poids à travers le système solaire
