Comme pour l’addition, les exemples présentés dans cet article portent sur des nombres plus grands que 100. Il est bien entendu possible d’utiliser les dominos pour la soustraction posée, avec des nombres inférieurs à 100.

La soustraction

Nous ne parlerons pas ici de l’intérêt de poser les soustractions. Gardons simplement à l’esprit qu’une soustraction ne doit être posée que si sa résolution par calcul mental est trop difficile.

Notons aussi que si soustraire c’est retirer, l’inverse n’est pas vrai. Les énoncés comme ceux de la recherche de l’état initial lors des transformations, en témoignent :

Alice a des économies. Elle retire 12 € pour acheter un cadeau. Il lui reste 7 €. Combien avait-elle d’économies ?

La soustraction n’est pas commutative : a – b ≠ b – a. L’opérande a est celui auquel on va retirer la valeur b. Si nous utilisons les dominos pour faire une soustraction, il nous faut bien sûr deux barres. Nous allons placer la valeur a dans la barre du haut.

Soit à réaliser la soustraction suivante :  523 – 345

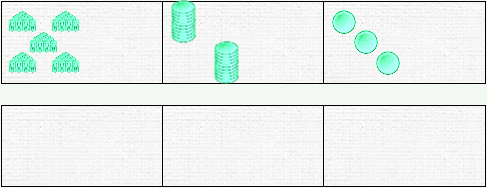
Pour réaliser la soustraction, nous allons retirer 345 pions de la barre du haut et les transférer dans la barre du bas. Ce qui reste dans la barre du haut sera le résultat. La valeur initiale a est donc détruite et est remplacée par la réponse.

Il n’y a pas de difficulté majeure pour effectuer le calcul avec les dominos. On va retirer des pions pour former la valeur 345 en bas, en utilisant la technique du passage de la dizaine, de la hiérarchie supérieure vers la hiérarchie inférieure : centaines vers dizaines et dizaines vers unités. En fait, l’activité de l’élève se résume à écrire 345 dans les dominos du bas avec les pions disponibles dans les dominos du haut, en faisant les conversions nécessaires, puis de lire le résultat sur la barre du haut. Avant de lire le résultat, on veillera à ce qu’il n’y ait pas 10 pions dans un domino de la barre. L’ordre dans lequel s’effectuent les transferts n’a aucune importance et l’élève n’effectue aucun calcul.

Voilà pour les dominos.  Passons maintenant en revue les deux techniques opératoires les plus répandues.

Deux techniques courantes de soustraction

La technique opératoire est une convention, un choix. Pendant longtemps, on apprenait à l’école uniquement la technique dite de la “conservation des écarts”. Elle est un peu compliquée, mais elle est compacte, et c’est sans doute pour cela qu’elle a été choisie. Mais à vrai dire, peu d’élèves la comprennent. Pendant des années, on apprenait la technique mécaniquement, on l’appliquait pour trouver le bon résultat et c’était suffisant – on n’en demandait pas plus. Le bon élève appliquait la technique de la même façon qu’il récitait par cœur la liste des affluents de la Seine. On ne lui demandait pas trop de comprendre, juste d’apprendre.

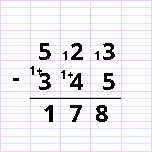
NB : dans la méthode la plus traditionnelle, on n’écrit pas le “+” après le 1 que l’on ajoute dans la ligne du milieu. Ce qui crée un peu de  confusion.

L’autre technique, anglo-saxonne, est celle dite du “cassage”. Elle a le mérite d’être plus facile à comprendre, mais demande peut-être un peu plus de soin à l’écriture.

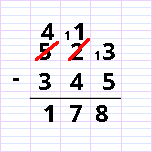
On le voit, la méthode du cassage est beaucoup plus proche de ce que l’on peut réaliser avec les dominos à numération décimale. Si l’on veut cependant amener les élèves à comprendre la méthode de conservation des écarts, c’est possible, mais – à mon avis – cela demande de comprendre d’abord la méthode du cassage. Voyons comment faire avec nos dominos.

Utilisation des dominos à numération décimale : du passage au cassage

Tout d’abord, préparons le terrain : écrivons l’opération à réaliser et plaçons le premier nombre dans les dominos du haut.

Comme pour l’addition, nous allons d’abord traiter les unités, puis les dizaines, puis les centaines.

Un exemple détaillé sur les unités

Nous devons placer 5 jetons dans le domino-unités du bas. Nous pouvons déjà transférer les trois premiers. Ensuite, comme d’habitude, nous allons prendre une pile du domino-dizaines pour la transférer dans le domino-unités du haut. Enfin, nous transférons deux jetons supplémentaires dans le domino-unités du bas.

Voici un petit résumé des 3 étapes de cette manipulation :

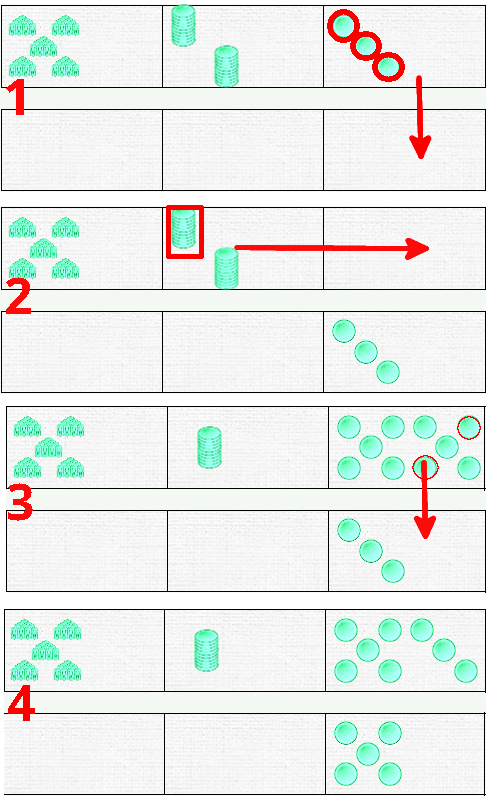
Normalement, si les élèves ont eu du temps pour manipuler les dominos, cette séquence d’actions ne devrait pas poser de problème. Voyons maintenant ce que cela donne sur notre opération posée.

Précisons tout de suite aux élèves que notre opération écrite va être différente de ce qu’il se passe avec les dominos.

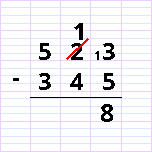
La première différence avec les dominos, à signaler, c’est que nous n’allons pas procéder unité par unité. C’est beaucoup trop long ! Nous allons donc essayer de faire la soustraction, constater que 3 est trop petit par rapport à 5 – en utilisant la formule consacrée : “trois moins cinq, on ne peut pas”, et passer la dizaine. “J’emprunte une dizaine – il en reste une”. On place le 1 au-dessus du 2-dizaine et on écrit le 1, petit, devant le 3. C’est là qu’il faut bien expliquer : cela correspond aux dix jetons que nous avons transférés dans le domino. En ajoutant ainsi 10 unités au trois déjà présentes, nous en obtenons 13 -cela revient donc à écrire “1” devant le 3.  C’est la deuxième différence avec le domino, qui, lui, ne peut pas contenir 13 jetons.

Ensuite, bien sûr, nous calculons 13-5 et marquons le résultat. On constate que c’est bien ce qui apparaît dans le domino-unités du haut.

On voit que l’intérêt du domino à numération décimale, c’est que les élèves ne devraient pas avoir de difficulté à comprendre le passage de la dizaine. On peut insister sur les différences opératoires entre le domino et la technique du cassage,  mais pas sur le passage lui-même, qui a été vu et revu lors du comptage et de l’addition.

Il suffit maintenant de poursuivre avec les dizaines, en alternant le travail avec les dominos et la représentation.

Du cassage à la conservation des écarts

Pour expliquer la méthode de conservation des écarts, il ne faut plus utiliser les dominos, car ils ne se prêtent guère à cette méthode. Observons plutôt ce que nous faisons dans l’opération avec le cassage. Dans notre exemple, nous ôtons une dizaine dans la colonne des dizaines. Pour cela, nous barrons le 2 et écrivons un 1 à la place. Mais on pourrait aussi laisser le 2 en place, et indiquer dans la ligne en-dessous que nous voulons ôter une dizaine : c’est le nombre 1 que nous ajoutons au nombre 4 déjà présent. Nous allons ôter 4 et 1, comme l’indique le signe “-” devant l’opération. Les deux écritures sont finalement équivalentes.