Présentation des booléens

Un booléen est une variable à deux états, à qui on attribue généralement les valeurs vrai ou faux. Dans un intégramme, l’utilisation des booléens permet de repérer des cases dont le comportement suit les mêmes règles : les cases repérées par un même booléen sont, soit toutes vraies, soit toutes fausses. Grâce à eux, un énoncé peut se coder directement dans les grilles. Une fois l’énoncé inscrit, il n’est plus nécessaire d’y revenir. La plupart des énoncés d’intégrammes peuvent se coder à l’aide des booléens : dès qu’un énoncé est précis, on peut le coder avec des booléens. Les énoncés imprécis ne permettent pas le codage immédiat. Dans la grille ci-dessous :

• Enzo est arrivé 2 minutes avant Océane est un énoncé précis
• Enzo est arrivé avant Océane est imprécis. Pour le coder il faut revenir plusieurs fois sur l’énoncé, à différentes étapes de la résolution.

Lorsque l’on résout  une énigme dans une revue, pour figurer un booléen, on peut écrire une lettre dans des cases. Il y a 26 lettres de l’alphabet, ce qui suffit largement. Voici par exemple, une façon de coder la proposition suivante dans l’énigme « Jogging à la plage » comme si elle figurait dans une revue :

Enzo est arrivé 2 minutes avant Océane.

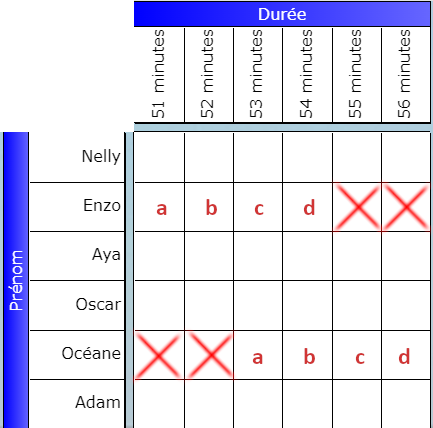
Ce codage établit les relations d’ordre entre les cases de la ligne Enzo et de la ligne Océane. Si Enzo court pendant 51 minutes, alors Océane court pendant 53 minutes – c’est le booléen a. Il en va de même pour les autres booléens. Nous voyons aussi que certaines valeurs ne sont pas possibles et sont matérialisées par le signe faux (la croix).

Ce codage avec des lettres tirées de l’alphabet fonctionne bien sur le papier où les cases sont petites.

Sur le site Actilud, cependant, j’ai choisi une autre représentation. Chaque booléen est formé par une lettre et un chiffre, et à chaque lettre est associée une couleur. Les booléens sont affichés sous forme de pastille colorée :

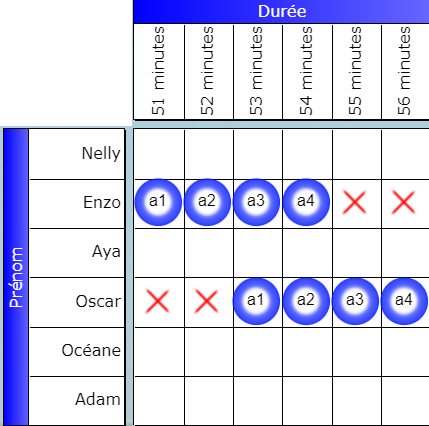
Le codage précédent avec les booléens {a, b, c, d} devient ici {a1, a2, a3, a4}.

L’avantage est d’augmenter la lisibilité générale de la grille. En effet, utiliser la même lettre associée à des chiffres différents pour une proposition donnée permet de repérer facilement les booléens qui relèvent de cette proposition, puisqu’à chaque lettre est associée une couleur donnée, ici le bleu foncé, ce qui la rend évidente d’un simple coup d’œil. Mais, d’un point de vue purement logique, les deux représentations sont strictement équivalentes.

Règles mathématiques de base

Nous aurons besoin de connaître les règles élémentaires de l’algèbre de Boole. Ces règles sont plutôt intuitives. Soit a et b deux booléens.

Règle du et

(a et b) est vrai seulement si a est vrai et b est vrai. Dans tous les autres cas (a et b) est faux.

a→ b↓	faux	vrai
faux	faux	faux
vrai	faux	vrai

Cette règle est citée pour mémoire. Nous l’utilisons implicitement dans les intégrammes. Prenons l’énigme « cerf-volants ». L’énoncé formé par la proposition composée Sandra joue pendant 30 minutes et a un cerf-volant bleu n’est vrai que si les deux éléments qui le constituent, Sandra joue pendant 30 minutes et Sandra a un cerf-volant bleu, sont vrais. Or, comme par principe les énoncés sont vrais, les éléments constitutifs sont donc toujours vrais.

Règle du ou exclusif (ou)

(a ou b) est vrai seulement si l’un des deux booléens est vrai. En particulier, (a ou b) est faux si a et b sont faux ou vrais tous deux.

Cette règle est très largement utilisée dans les intégrammes; elle fonde les alternatives.

a→ b↓	faux	vrai
faux	faux	vrai
vrai	vrai	faux

Si a et b sont vrais tous deux, (a ou b) est faux. C’est tout à fait le cas dans les alternatives. Le chapitre sur les alternatives est entièrement consacré à cette règle, alors nous ne nous étendrons pas sur le sujet. Prenons un exemple simple pour comprendre :

Nelly pilote son cerf-volant pendant 30 minutes ou pendant 50 minutes.

Nous voyons bien que Nelly ne peut pas piloter à la fois pendant 30 et 50 minutes. Une seule de ces deux possibilités est la bonne. C’est un cas typique de ou exclusif. En Français, on peut traduire le ou exclusif par la locution : soit…, soit…, mais au prix d’une certaine lourdeur dans la phrase :

Nelly pilote un cerf-volant soit pendant 30 minutes, soit pendant 50 minutes.

Notons qu’en langue française, la locution ou prend souvent la signification mathématique du ou exclusif. 

Voici la vidéo associée; si elle ne s’affiche pas, actualisez la page.