Le Sudoku permet de travailler l’organisation de l’espace en respectant une contrainte, celle de l’unicité des pièces dans chaque ligne, colonne et région. C’est un excellent exercice d’observation, de concentration et de logique. Il permet aussi d’introduire des notions de lignes et colonnes, donc d’horizontalité et verticalité. C’est aussi un très bon moyen de mémoriser les chiffres.

Règle du jeu

Le Sudoku est formé par une grille carrée contenant n x n cases. Sur Actilud, on a le choix entre des grilles 4×4, 6×6 et 9×9. Chaque case peut contenir un signe; sur le site, ce sont, soit des fruits, soit des chiffres. La grille est organisée en lignes, colonnes et régions, qui sont des zones rectangulaires contenant autant de cases qu’une ligne ou une colonne. Un signe ne peut être présent qu’une seule fois dans chaque ligne, colonne et région. Au départ, un certain nombre de signes sont posés dans la grille; il s’agit de la compléter en respectant la contrainte de position.

Les Sudokus sur Actilud

Ils sont évidemment à but pédagogique, donc pas spécialement difficiles ! N’espérez pas avoir besoin de techniques avancées pour les résoudre ! Ils sont générés aléatoirement par un algorithme qui veille à ce qu’il soit toujours possible de trouver une case en employant les deux stratégies exposées ci-dessous.

Notion de candidat

Un candidat est le terme usuel pour désigner les signes qui sont susceptibles d’être placés dans une case. Dans le Sudoku ci-dessus, la case en bas à droite a deux candidats: la prune et le kiwi. En effet, ces deux fruits ne sont présents ni dans la ligne, ni dans la colonne, ni dans la région qui contiennent cette case. Par cette seule constatation, il n’est pas possible de trancher pour le moment. Par contre, la case juste au-dessus ne peut contenir qu’un seul candidat: la fraise, puisque la ligne contient déjà les trois autres fruits. La fraise est donc le candidat unique pour cette case: on peut la placer.

Un peu de vocabulaire: une zone est une ligne, une colonne ou une région. Une rangée est une ligne ou une colonne.

Deux stratégies pour trouver les candidats uniques

L’examen systématique des cases par dénombrement

C’est la technique de base, que je viens d’expliquer à l’instant. On observe une case, on cherche les signes présents dans les zones qui la contiennent. S’il n’y en a qu’un seul possible, on le place .

Cette technique fonctionne bien sur les grilles 4×4 ou 6×6; mais elle est assez fastidieuse. Elle demande de l’observation et beaucoup de concentration. Plus il y a de signes, plus elle est difficile. Paradoxalement, elle est encore plus difficile sur des grilles 9×9 avec des fruits, car lorsque l’on connaît les chiffres, il est plus facile de les mémoriser. Si vous êtes pédagogue, il pourrait être intéressant de tester vous-même les grilles avec des fruits; vous pourrez ainsi mieux apprécier la difficulté qu’éprouvent élèves lorsqu’on leur demande d’utiliser les chiffres alors qu’ils les connaissent à peine.

La technique topologique

Elle s’effectue par une visualisation des zones de de leur intersection; elle donne de meilleurs résultats. Il faut amener les élèves à l’utiliser. Reprenons l’exemple ci-dessus et observons certaines rangées contenant le kiwi :

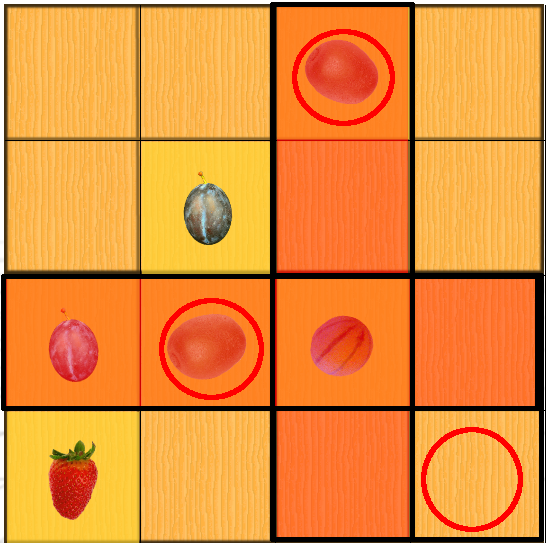
Les cases restantes dans la ligne contenant le kiwi ne peuvent en contenir un autre; de même pour la colonne. Dans la région du bas à droite, il n’y a plus qu’une seule case possible pour contenir le kiwi: celle marquée par un cercle vide. Maintenant, nous pouvons placer le kiwi et éliminer la prune qui pourtant était candidate avec la technique précédente.

La technique topologique repose donc sur l’intersection entre lignes, colonnes, régions. Le minimum étant bien sûr d’utiliser deux zones.  Voyez ce qu’il se passe avec la prune: l’intersection d’une ligne et d’une région suffit pour révéler une case :

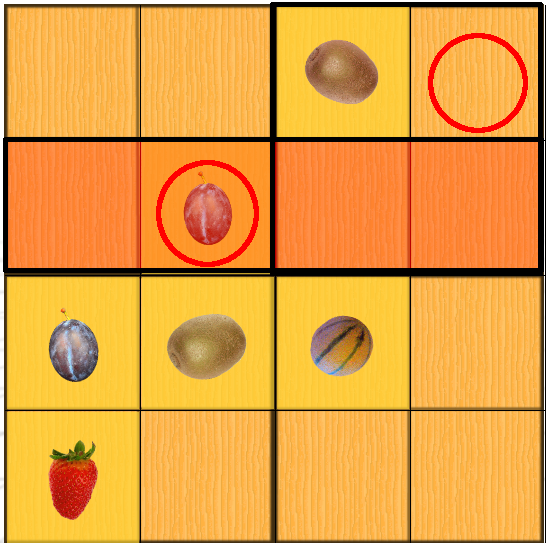Quelquefois on doit utiliser plusieurs lignes, colonnes ou régions pour trouver une case. C’est surtout le cas dans les grandes grilles.

Dans les grilles 9×9 on cherche en priorité les signes les plus représentés, car c’est avec eux que nous avons le plus de chances d’utiliser notre technique topologique. Pour cela, on peut compter le nombre de signes et prendre ceux qui sont en nombre le plus important. Mais on peut aussi se fier à notre perception globale de la situation. Le cerveau est en effet tout à fait capable de percevoir les signes parmi les plus nombreux sans avoir à les compter.

Observez le chiffre 1 dans le Sudoku ci-dessous. Nous voyons que deux colonnes, une ligne et une région forment une intersection qui mettent en évidence une case qui doit le contenir; alors que si nous avions utilisé la technique du dénombrement des candidats, nous aurions trouvé deux autres candidats possibles : le 4 et le 6.

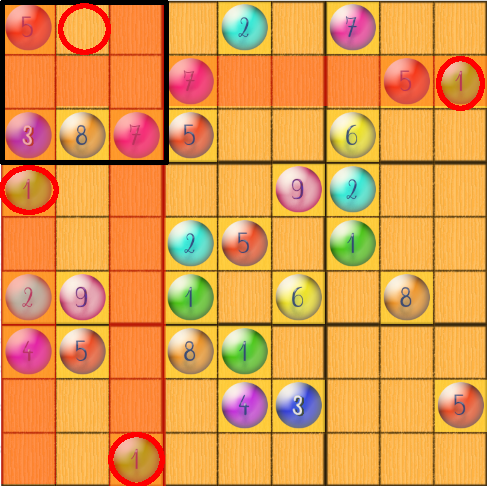Dans les grandes grilles, on commence par appliquer la technique topologique; ensuite, s’il reste des cases, on utilise la technique du dénombrement – comme les cases à dénombrer sont moins nombreuses, la technique est moins fatigante !

Démarrer l’activité.