La machine de Turing est un modèle mathématique mis au point par le célèbre mathématicien Alan Turing en 1936. Généralement, on présente le modèle comme un moyen de démontrer les capacités d’un ordinateur. Ce qu’une machine de Turing peut faire, un ordinateur peut – ou pourra – le faire. Ce qu’une machine de Turing ne peut pas faire, aucun ordinateur ne pourra jamais le réaliser.
Cette présentation est exacte mais restrictive. En fait, la machine de Turing permet de définir ce qui est calculable, que ce soit par un ordinateur, un humain… ou un extra-terrestre, du moins si les lois de l’univers sont les mêmes partout.
Ainsi, lorsqu’un mathématicien réalise une machine de Turing destinée à accomplir une tâche, il démontre que la tâche est calculable, et produit donc un théorème. Celui-ci peut être réutilisé dans une démonstration plus vaste.
Intérêt pédagogique
Le fonctionnement d’une machine de Turing est très simple à comprendre et son apprentissage ne prend que quelques minutes. Mais les programmes à développer demandent une réelle capacité d’analyse, d’organisation et d’anticipation. Les quelques défis que nous proposons sur Actilud en sont des exemples.
Fonctionnement du modèle
La machine se présente comme une bande, de taille infinie, découpée en cases. Chaque case peut contenir un signe – une lettre, un chiffre, une image, peu importe. Le nombre de signes possibles est quelconque, mais fini, et constitue la collection.

Sur cette bande se promène une tête de lecture. Celle-ci peut lire un signe, le remplacer par un autre, et se déplacer d’une case vers la droite ou vers la gauche. Elle est contrôlée par un programme. Sa vitesse d’exécution est infinie (c’est un modèle !)

La machine possède un nombre quelconque, mais fini, d’états. Par convention, les états sont symbolisés par la lettre Q et chaque état possède un nom par défaut : q0, q1, q2… Les états permettent de sélectionner les instructions à exécuter. Le premier état de la liste est l’état par défaut, dans lequel la machine va se placer au démarrage du traitement.
Chaque instruction est une condition suivie par une action, codée de la manière suivante :
Si la machine se trouve dans l’état q0, et que la tête lit le signe X, y écrire le signe Y, déplacer la tête d’une case à gauche ou à droite (ou rester en place), et passer à l’état q1.
Une instruction est exécutée lorsque les conditions sont remplies : l’état et le signe correspondent. Une fois l’instruction exécutée, la machine parcourt à nouveau la liste des instructions, et ainsi de suite. La machine s’arrête lorsqu’aucune instruction n’a pu être exécutée.
Voilà c’est tout. Quand je disais que l’apprentissage était court…
Un exemple pour comprendre
Soit une bande contenant un certain nombre de bâtons contigus. Réalisons un programme qui va ajouter un nouveau bâton à la série.
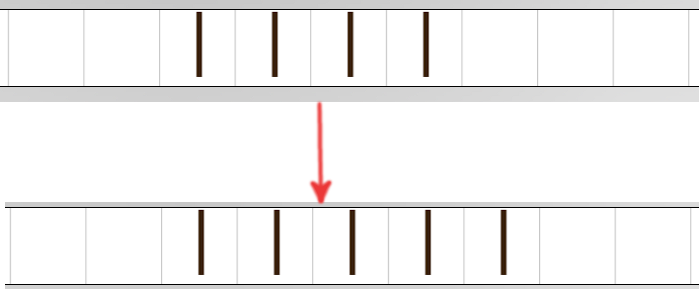
Nous positionnons la tête sur un des bâtons et démarrons la machine dans l’état q0. Voici les instructions :
q0, | , | , →, q0
q0, ☐, |, stop
Explications
Si la machine se trouve dans l’état q0 et que la tête lit un bâton (signe « | »), écrire un bâton, déplacer la tête vers la droite (c’est la flèche), rester dans l’état q0. Le fait de réécrire le même signe dans une case ne change donc rien à la bande. C’est le moyen de « survoler » une case sans la modifier : on réécrit son contenu.
Si la machine est dans l’état q0, qu’elle lit un blanc, c’est à dire une case « vide » matérialisée par ☐, alors écrire un bâton, se placer dans l’état stop. Comme cet état n’est pas défini dans le programme, la machine s’arrête. Le choix du nom n’a pas d’importance, nous aurions pu appeler cet état autrement : q1, arrêt… Pour arrêter volontairement une machine, il suffit d’invoquer un état qui n’existe pas.
Notons qu’en informatique, un « vide » est toujours quelque-chose. Dans le modèle de Turing, les cases « vides » sont en fait remplies de signes « blancs ».
On le voit, ici il n’y a qu’un seul état actif. De fait, on peut simplifier l’écriture en restant dans le même état :
|,|,→
☐,|, stop
Que fait la machine ? Vous l’avez compris: tant que la tête lit un bâton, la machine déplace la tête vers la droite. Dès qu’elle trouve une case vide, elle y écrit un bâton et s’arrête. La machine ajoute donc un bâton à la fin de la série et s’arrête sur celui-ci.
Les machines de Turing sur Actilud
La bande
Évidemment, la bande a une taille limitée. Sur Actilud, il y a 1000 cases, ce qui permet déjà de s’amuser un peu. En conséquence, notre machine peut rencontrer une erreur « fatale », lorsque la tête tente de sortir de la bande, par la gauche ou par la droite. Dans ce cas, tout le processus s’interrompt.
Une bande n’est pas « vide ». En fait, lorsqu’on « efface » la bande, on remplit chaque case avec un signe « blanc ». À part cela, les signes « blancs » sont traités exactement comme les autres signes de la collection.
La tête de lecture
Pas de vitesse infinie ! La tête peut fonctionner en mode « pas à pas », en deux temps, ce qui est le mode pédagogique par excellence. Elle peut aussi avancer avec deux vitesses, ou fonctionner en tâche de fond, au maximum de la vitesse possible dans le navigateur.
La collection
La collection sur Actilud contient des images de fruits et légumes, des émoticônes, des lettres majuscules et minuscules, des chiffres, quelques symboles. Cela permet de réaliser des programmes conséquents. Lorsque l’on écrit un programme, il est bon de préciser la collection sur laquelle celui-ci travaille. Par exemple : C={[a-z],[A-Z],[0-9],☐} – la collection se compose des lettres minuscules a à z, majuscules A à Z, des chiffres de 0 à 9 et du blanc.
Les états
Le nombre d’états n’est pas limité, mais il dépend bien sûr de la taille de la mémoire disponible sur votre ordinateur. Pour la simplicité, nous avons regroupé les instructions dans les états. Il n’est donc pas nécessaire de faire référence à l’état de départ dans la programmation des instructions, puisqu’elles sont raccrochées à cet état.
On peut se contenter des noms par défaut (q0, q1,…) mais il est possible de donner des noms particuliers à chaque état.
Les machines
Dans chaque instruction on peut spécifier, en plus de l’état de destination, le nom d’une machine à lancer. Votre programme peut donc contenir du code pour plusieurs machines, qui peuvent s’imbriquer : une machine A lance une machine B, qui lance une machine C…
C’est l’idée du « théorème » précédemment évoquée : par exemple, vous avez réalisé une machine qui décrémente un entier naturel. Vous pouvez la réutiliser dans une machine qui transforme un entier naturel en une suite de bâtons.
Lancer une machine à l’intérieur d’une machine n’est pas une entorse au modèle : en effet, Turing a démontré que l’on peut créer une machine universelle, c’est à dire une machine de Turing qui simule le fonctionnement d’une machine de Turing décrite sur la bande. Mais, comme il est illusoire de réaliser ceci sur notre petite bande de 1000 cases, je propose donc de lancer de nouvelles machines à l’intérieur des instructions.
Cela permet surtout de réutiliser du code. Bien sûr, il n’y a aucune obligation d’utiliser cette fonctionnalité.
Si vous êtes débutant(e), vous allez certainement commencer par coder une seule machine. Vous pouvez ignorer les deux paragraphes suivants, appel des machines et récursion. Vous y reviendrez plus tard, quand vous serez plus aguerri(e).
Appel des machines
Lorsqu’une machine en appelle une autre, la machine appelante est stockée dans une pile : c’est un emplacement en mémoire qui contient chaque machine appelante, dans l’ordre d’arrivée. Lorsque la machine appelée a terminé, la machine appelante est sortie de la pile et son exécution reprend.
Jusqu’à 500 machines peuvent être stockées dans la pile. Au-delà, le programme s’interrompt avec une erreur fatale : « débordement de pile ».
Une machine appelée démarre toujours dans son état par défaut.
Lorsqu’une machine appelée s’arrête « normalement », c’est à dire hors erreur fatale, elle rend la main à la machine appelante.
La machine appelante se retrouve dans l’état qu’elle avait au moment de l’appel de la machine appelée.
Lorsqu’une machine appelée rencontre une erreur fatale, tout le processus s’arrête et la pile est vidée.
Récursion
Le débordement de pile peut être un handicap lorsque l’on utilise des formules récursives. Mais, si on place la machine appelante dans un état d’arrêt juste avant de lancer une nouvelle machine, la pile n’est pas sollicitée.

L’exemple ci-dessus montre une instruction. Si la tête lit un 1, il faut mettre un 1, ne pas bouger, aller dans l’état « stop » qui est notre état d’arrêt, et lancer la machine qui s’appelle « Décrémente », que l’on a programmée par ailleurs. Ici la pile n’est pas sollicitée, car il n’y a pas lieu d’empiler la machine actuelle qui est arrêtée juste avant le démarrage de la machine appelée.
Si vous utilisez la récursion, analysez bien votre programme : très souvent, on n’a effectivement pas besoin de relancer la machine appelante, à la fin de l’exécution de la machine appelée.
L’optimisation de la pile est automatique dans bien des langages évolués; je pense bien sûr au Javascript utilisé sur le site, mais aussi à ce cher vieux Logo, qui fait un usage immodéré de la récursion.
Les instructions
Comme on le voit dans l’exemple ci-dessus, tout est visuel sur Actilud. Les instructions se manipulent comme les autres objets du site.
Signe particulier…
J’ai programmé un signe particulier qui est une petite extension au modèle : le signe ∀ qui signifie « pour tout » ou « quel que soit », en maths.
On ne peut pas poser ce signe sur la bande; il est réservé aux instructions.
 La signification de ∀ dépend de sa position dans l’instruction.
La signification de ∀ dépend de sa position dans l’instruction.
En première position, le signe ∀ signifie: « pour tout signe lu » ou « quel que soit le signe lu » – donc la condition est toujours vraie si la machine rencontre cette instruction, y compris pour le signe « blanc ».
En seconde position, le signe ∀ signifie: « écrire sur la bande le signe lu, quel qu’il soit ».
Notre instruction, ici, signifie donc: quel que soit le signe lu, écrire le même signe sur la bande (autrement dit, il ne se passe rien apparemment sur la bande), aller à droite, et rester dans le même état puisqu’aucun état n’est spécifié.
Cette écriture est pratique car elle permet d’économiser des tas de lignes de code. C’est pourquoi je l’ai ajoutée. Elle est compatible avec le modèle, car le symbole ∀ remplace une série d’instructions presque identiques : si ma collection est formée de chiffres de 0 à 9 et du blanc, le signe ∀ permet d’éviter l’écriture de 10 instructions.
On constate qu’après elle, aucune autre instruction ne peut s’exécuter, car elle est toujours vraie. On doit donc la placer en fin de liste et placer les exceptions à la règle avant celle-ci. Celles et ceux qui ont déjà programmé un pare-feu apprécieront…
Les deux instructions ci-dessous sont équivalentes :

Dans les deux cas, la tête ré-écrit la fraise et se déplace à gauche. La première écriture est intéressante dans l’interface d’Actilud, car lorsqu’on a beaucoup d’objets dans la même situation, on peut produire rapidement un lot d’instructions de ce type en changeant l’objet de gauche mais en laissant le signe ∀ à droite. Mais elle est moins lisible que la seconde écriture; avec un clic de plus dans l’éditeur, sur la flèche rouge de transfert, on peut recopier le signe de gauche à la position de droite.
Souvent, lorsque l’on manipule des nombres, on doit se placer au début ou à la fin du nombre étudié avant de démarrer un traitement. Voici un un exemple de machine qui parcourt un entier naturel, sans le modifier, jusqu’à atteindre la droite du nombre. Il y a un chiffre par case et les chiffres se suivent. Au départ, la tête est placée quelque part sur un des chiffres formant le nombre.
Sans le signe ∀ :

Avec le signe ∀ :

C’est plus court, n’est-ce pas ?
Attention tout de même, les deux programmes ne sont pas tout à fait équivalents ! Tout dépend de la collection !
Sur une collection limitée aux 10 chiffres et au blanc, les deux programmes fonctionnent de la même façon :
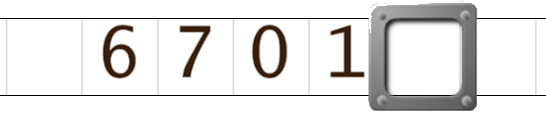
Mais voici un cas où les deux programmes diffèrent !
On commence toujours sur le premier chiffre à gauche, le chiffre « 2 » de 24.
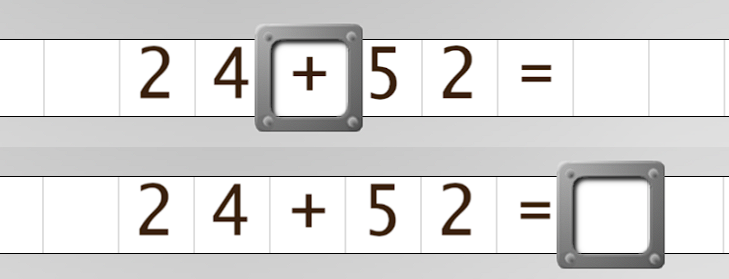
Le premier programme, sur la bande du haut, se termine après le 24, sur le signe « + », et correspond à notre souhait. Le second, sur la bande du bas, se termine tout à la fin de la formule, sur le premier blanc rencontré. Selon l’effet recherché ce peut être souhaitable, mais il convient de bien le préciser dans la description de la machine.
Listage
On peut lister les machines programmées sous une forme moins ludique, mais plus compacte. Le listage n’est pas une sauvegarde car on ne peut pas recréer automatiquement les machines à partir du listage, mais il permet de conserver une trace de son travail et surtout d’être à l’aise pour y réfléchir. On peut aussi s’inspirer de cette écriture pour préparer le travail, ou trouver des bugs. Voilà ce que donne le listage du programme sans ∀ :
Machine : [AllerDroite]
# Se déplacer à l’intérieur d’un entier naturel jusqu’à la première case à droite du nombre.
État : VaDroite
# Se déplace à droite sur chaque chiffre.
VaDroite, 0 , 0 , → , VaDroite
VaDroite, 1 , 1 , → , VaDroite
VaDroite, 2 , 2 , → , VaDroite
VaDroite, 3 , 3 , → , VaDroite
VaDroite, 4 , 4 , → , VaDroite
VaDroite, 5 , 5 , → , VaDroite
VaDroite, 6 , 6 , → , VaDroite
VaDroite, 7 , 7 , → , VaDroite
VaDroite, 8 , 8 , → , VaDroite
VaDroite, 9 , 9 , → , VaDroite
Pour conserver un listage, faites un copier/coller vers un document.
Sauvegarde
Bien entendu, votre travail peut être sauvegardé; rendez-vous dans le menu « exécuter » et cliquez sur l’icône de la disquette. Là, vous pouvez sauvegarder les machines que vous venez de définir et même la bande. Pour les connaisseurs, le fichier obtenu est un fichier de type json assorti d’un code de hachage, pour éviter que l’on modifie intempestivement le contenu du fichier; le but est d’éviter les plantages si on fait n’importe quoi. Ne modifiez donc pas le fichier à la main, il sera refusé.
Le fichier est disponible dans le dossier de téléchargements de votre appareil.
Pour lire un fichier, utiliser l’icône ouvrir fichier dans la barre d’outils. Là, vous pouvez choisir les modalités de chargement. Une modalité pratique permet d’ajouter les machines chargées à celles déjà présentes. Cela permet donc de réutiliser facilement une machine dans un nouveau projet.
Confidentialité
Votre travail a lieu exclusivement sur la machine locale. Aucune sauvegarde n’est effectuée sur le serveur; il ne récupère pas vos données. Lorsque vous réalisez une sauvegarde, c’est le programme qui est dans votre navigateur qui envoie le fichier; ce n’est pas le serveur.
Nos défis
Vous trouverez sur le site d’information quelques propositions de défis de programmation; bien sûr la liste n’est pas exhaustive.
Les étapes pour programmer une machine
La toute première étape devrait avoir lieu sur papier, au crayon et à la gomme ! C’est la phase de conception. Seuls les programmeurs aguerris peuvent s’en passer ! Donc, pour qu’un débutant se serve convenablement de la machine il faut impérativement réaliser ce travail préparatoire.
La mise en place des instructions se fait en trois étapes. Tout d’abord, on crée une machine. Puis, dans cette machine, on créée un état. Enfin, dans cet état, on définit des instructions.
Comme écrit plus haut, les instructions sont rassemblées dans les états, ce qui simplifie les tests et le classement. Dans une instruction, on ne fait donc jamais de test sur l’état courant de la machine, puisque seules les instructions correspondant à l’état en cours sont exécutées.
On peut revenir en arrière et créer un nouvel état, avec ses propres instructions, autant de fois que nécessaire. On peut dupliquer les états, les fusionner. De même pour les machines. Tout est visuel sur le site et grâce à de nombreux boutons de contrôle, la programmation est au moins aussi efficace, voire plus, qu’avec un éditeur de texte… avec un peu d’entraînement bien sûr. Voyez la vidéo ci-dessous.
Le mode d’emploi
Voici une vidéo muette, courte, en deux langues, pour comprendre comment se servir de la machine sur Actilud. Une fois n’est pas coutume, c’est mieux et plus rapide qu’une description écrite. Si elle ne s’affiche pas, actualisez la page.

