Addition des bâtons
L’arithmétique des bâtons est sans doute la plus facile à mettre en œuvre avec une machine de Turing. La collection à utiliser est C={ ☐, |, X, =, +}.
On écrit sur la bande une addition avec des bâtons, comme par exemple: ||||+||=
Le résultat doit être de la forme : ||||+||=||||||
On commence sur le signe = ou sur le bâton immédiatement à sa droite, au choix. On doit terminer sur le premier blanc à droite de la réponse.
Description
La tête se rend d’abord à gauche. Si elle rencontre un X, le signe + ou le signe =, elle continue à gauche. Si elle rencontre un bâton, elle le transforme en X et se dirige vers la droite, jusqu’à ce qu’elle rencontre un blanc. Là, elle écrit un X et recommence son déplacement vers la gauche. Si en allant à gauche elle finit par trouver un blanc, elle retourne vers la droite en transformant tous les X en bâton et s’arrête sur le premier blanc.
Décrémentation universelle d’un entier naturel
Nous avons souvent besoin d’évaluer la valeur d’un nombre et pour cela, le plus facile avec la machine de Turing est de décrémenter le nombre. Nous allons réaliser une machine de Turing réutilisable dans des programmes plus importants. Il s’agit de décrémenter un entier naturel posé sur la bande à raison d’un chiffre par case. Si l’entier arrive à sa valeur finale, 0, alors il faut effacer le 0; s’il reste plusieurs 0 consécutifs, il faut tous les effacer. Le programme doit s’arrêter sur le dernier chiffre, ou sur le dernier blanc qu’il a écrit s’il a tout effacé. Pourquoi ? parce qu’un autre programme qui utiliserait notre machine doit “savoir” si la machine a effectué une décrémentation ou non. Tant qu’elle s’arrête sur un chiffre, c’est que la décrémentation a eu lieu. Si elle s’arrête sur un blanc, c’est que la décrémentation est terminée. C’est ainsi que notre machine fait passer l’information à la machine appelante.
Notre machine doit aussi prévoir la possibilité qu’il existe des signes différents du blanc de part et d’autre du nombre. Donc on utilisera de préférence le signe ∀ pour repérer tout signe différent des chiffres.
Voici quelques exemples; la position de la tête indique le point de départ et le point d’arrivée.
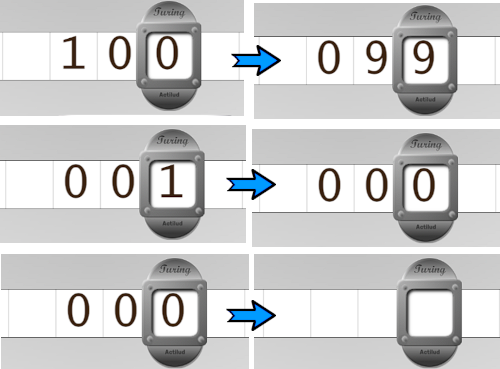
Solution : la machine à décrémenter (spoiler)
Machine : [Décrémenteur]
# Décrémente un entier naturel. S’il reste des 0, les remplace par des blancs. S’arrête toujours sur le dernier chiffre, ou le blanc.
# Début : sur la donnée la plus à droite
# Fin : sur la donnée la plus à droiteÉtat : Décrément
Décrément, 9 , 8 , → , transitDroite
Décrément, 8 , 7 , → , transitDroite
Décrément, 7 , 6 , → , transitDroite
Décrément, 6 , 5 , → , transitDroite
Décrément, 5 , 4 , → , transitDroite
Décrément, 4 , 3 , → , transitDroite
Décrément, 3 , 2 , → , transitDroite
Décrément, 2 , 1 , → , transitDroite
Décrément, 1 , 0 , → , transitDroite
Décrément, 0 , 9 , ← , Décrément
Décrément, ∀ , ∀ , → , efface9État : transitDroite
# Saute tous les chiffres jusqu’au dernier. S’arrête sur le dernier chiffre.
transitDroite, 9 , 9 , → , transitDroite
transitDroite, 8 , 8 , → , transitDroite
transitDroite, 7 , 7 , → , transitDroite
transitDroite, 6 , 6 , → , transitDroite
transitDroite, 5 , 5 , → , transitDroite
transitDroite, 4 , 4 , → , transitDroite
transitDroite, 3 , 3 , → , transitDroite
transitDroite, 2 , 2 , → , transitDroite
transitDroite, 1 , 1 , → , transitDroite
transitDroite, 0 , 0 , → , transitDroite
transitDroite, ∀ , ∀ , ← , stopÉtat : efface9
# Efface tous les 9 consécutifs; s’arrête sur le dernier blanc posé.
efface9, 9 , ☐ , → , efface9
efface9, ∀ , ∀ , ← , stop
Poser N pommes !
Dans certains cas, on a besoin d’un grand nombre d’objets sur la bande pour tester un programme. Par exemple, il faudrait 100 pommes pour vérifier si un programme de comptage passe bien de 1 à 100. Évidemment, si on a du temps à perdre, on peut placer manuellement les pommes une à une sur la bande, et tester le programme.
Mais on peut aussi réaliser un programme de Turing ! On écrit un entier naturel supérieur à 0 sur la bande, la tête est placée sur le dernier chiffre.
Et voici la situation finale; la tête se retrouve à l’arrêt, sur la première pomme d’une série. Le nombre initialement écrit sur la bande est effacé. Les pommes sont placées à droite du nombre initial.
![]()
Pratique, non ? Pour exécuter le programme, une fois la phase de mise au point terminée, il est conseillé d’utiliser le mode de fonctionnement le plus rapide – le bouton “cheval à l’arrivée” par exemple. Le temps d’exécution augmente en effet très rapidement en fonction du nombre de pommes.
c= {[0-9],☐,pomme}
Solution 1: tout dans la même machine (spoiler).
Machine : [Répéteur]
# Décrémente un entier naturel et place autant de pommes à droite de ce nombre.
État : Décrémenter
# Décrémente un nombre
Décrémenter, 9 , 8 , → , TransitDroite
Décrémenter, 8 , 7 , → , TransitDroite
Décrémenter, 7 , 6 , → , TransitDroite
Décrémenter, 6 , 5 , → , TransitDroite
Décrémenter, 5 , 4 , → , TransitDroite
Décrémenter, 4 , 3 , → , TransitDroite
Décrémenter, 3 , 2 , → , TransitDroite
Décrémenter, 2 , 1 , → , TransitDroite
Décrémenter, 1 , 0 , → , TransitDroite
Décrémenter, 0 , 9 , ← , Décrémenter
Décrémenter, ☐ , ☐ , → , Supprimer9
État : Supprimer9
# Supprime tous les 9 et stop.
Supprimer9, 9 , ☐ , → , Supprimer9
État : TransitDroite
TransitDroite, ☐ , pomme , ← , TransitGauche
TransitDroite, ∀ , ∀ , → , TransitDroite
État : TransitGauche
TransitGauche, pomme , pomme , ← , TransitGauche
TransitGauche, ∀ , ∀ , Décrémenter
Solution 2: deux machines, celle qui décrémente est une reprise du précédent exercice (spoiler)
Machine : [AjouterPommes]
# Début : sur la donnée la plus à droite
# Fin : sur la donnée la plus à droiteÉtat : lancerDécrémenteur
lancerDécrémenteur, ☐ , ☐ , stop
lancerDécrémenteur, ∀ , ∀ , évaluation, [Décrémenteur]État : évaluation
# Evalue le résultat du décrémenteur. Si c’est un nombre, il faut ajouter une pomme. Sinon, il faut s’arrêter.
évaluation, 0 , 0 , → , ajouterPomme
évaluation, 1 , 1 , → , ajouterPomme
évaluation, 2 , 2 , → , ajouterPomme
évaluation, 3 , 3 , → , ajouterPomme
évaluation, 4 , 4 , → , ajouterPomme
évaluation, 5 , 5 , → , ajouterPomme
évaluation, 6 , 6 , → , ajouterPomme
évaluation, 7 , 7 , → , ajouterPomme
évaluation, 8 , 8 , → , ajouterPomme
évaluation, 9 , 9 , → , ajouterPommeÉtat : ajouterPomme
# Ajoute une pomme à la suite de la série de pommes, s’il y a de la place.
ajouterPomme, pomme , pomme , → , ajouterPomme
ajouterPomme, ☐ , pomme , ← , retourArrièreÉtat : retourArrière
# Revient en arrière jusqu’au nombre initial.
retourArrière, pomme , pomme , ← , retourArrière
retourArrière, ∀ , ∀ , lancerDécrémenteur
#——————————
Machine : [Décrémenteur]
# Décrémente un entier naturel. S’il reste des 0, les remplace par des blancs. S’arrête toujours sur le dernier chiffre, ou le blanc.
# Début : sur la donnée la plus à droite
# Fin : sur la donnée la plus à droiteÉtat : Décrément
Décrément, 9 , 8 , → , transitDroite
Décrément, 8 , 7 , → , transitDroite
Décrément, 7 , 6 , → , transitDroite
Décrément, 6 , 5 , → , transitDroite
Décrément, 5 , 4 , → , transitDroite
Décrément, 4 , 3 , → , transitDroite
Décrément, 3 , 2 , → , transitDroite
Décrément, 2 , 1 , → , transitDroite
Décrément, 1 , 0 , → , transitDroite
Décrément, 0 , 9 , ← , Décrément
Décrément, ∀ , ∀ , → , efface9État : transitDroite
# Saute tous les chiffres jusqu’au dernier. S’arrête sur le dernier chiffre.
transitDroite, 9 , 9 , → , transitDroite
transitDroite, 8 , 8 , → , transitDroite
transitDroite, 7 , 7 , → , transitDroite
transitDroite, 6 , 6 , → , transitDroite
transitDroite, 5 , 5 , → , transitDroite
transitDroite, 4 , 4 , → , transitDroite
transitDroite, 3 , 3 , → , transitDroite
transitDroite, 2 , 2 , → , transitDroite
transitDroite, 1 , 1 , → , transitDroite
transitDroite, 0 , 0 , → , transitDroite
transitDroite, ∀ , ∀ , ← , stopÉtat : efface9
# Efface tous les 9 consécutifs; s’arrête sur le dernier blanc posé.
efface9, 9 , ☐ , → , efface9
efface9, ∀ , ∀ , ← , stop
Déplacer un entier naturel vers la gauche
Même si les possibilités de mise en forme sont très limitées sur notre bande, la présentation compte ! Souvent, après une série de conversions, on doit déplacer le résultat, un entier naturel, vers une nouvelle position, en général immédiatement à droite d’un signe =. Pour corser la difficulté, nous posons qu’il peut y avoir n’importe quoi entre le nombre et le signe =, y compris des chiffres qui ne font pas partie du nombre à transférer. Lors du déplacement, tous les signes présents entre le nombre et le signe = doivent être effacés (c-à-d remplacés par un blanc). La machine doit s’arrêter sur le signe =. Ici, le symbole ∀ sera d’une grande utilité. Au départ, la tête doit être positionnée sur le premier chiffre formant ce nombre à déplacer (donc le chiffre de gauche). À la fin, elle doit être positionnée sur le signe “=”.
Exemple: situation de départ : =☐ 1 2 3 x y z t 5 8 4☐ ☐ ☐ (tête positionnée sur le 5 : déplacer 584)
Situation d’arrivée: =584☐ ☐ ☐ ☐ ☐ ☐ ☐ ☐ ☐ ☐ ☐
Bien évidemment, la machine ne doit pas se “planter” si le nombre est déjà correctement positionné à la suite du signe =. Et si vous utilisez ma technique du X et Y décrite ci-dessous, elle ne doit pas planter non plus s’il n’y a qu’une seule case entre le = et le premier chiffre.
La collection est C={toute la collection de signes définis sur Actilud}.
Ici, il va falloir mémoriser les chiffres que l’on déplace. Avec la machine de Turing, la seule possibilité de mémoriser une information est d’utiliser un état pour chaque information à mémoriser. Parmi les états nécessaires au fonctionnement, Il faudra en créer autant qu’il y a de signes à transporter, soit 10.
Bien sûr il y a plusieurs façons de réaliser le programme. Programmer certains états est assez répétitif; alors, pour économiser le nombre d’états à programmer, mon idée a été la suivante. Tout d’abord, on nettoie bien la bande entre le signe = et le premier chiffre. On délimite l’espace entre le = et le premier chiffre par deux lettres, X et Y. Le segment [X,Y] se déplace au fur et à mesure que l’on déplace un chiffre à la suite de ceux déjà placés à droite de =. La lettre Y permet de tester la fin du programme : s’il n’y a plus de chiffre à droite du Y c’est terminé. X marque l’emplacement de la case dans laquelle il faut déposer un chiffre. Si on n’utilise pas cette astuce, il faut créer 10 états supplémentaires rien que pour déposer un chiffre à droite du signe = ! (notez qu’au lieu d’utiliser X et Y, on aurait pu utiliser uniquement X).
Voici le listing (spoiler)
Machine : [DéplaceNombreVersEgalGauche]
# Début : sur le chiffre le plus à gauche du nombre à transférer
# Fin : sur le signe =État : initialiser
# Quitter le chiffre pointé pour préparer la bande
initialiser, ∀ , ∀ , ← , remplir blancsÉtat : remplir blancs
# Remplir les cases à gauche de blanc jusqu’au signe =
remplir blancs, ‘=’ , ‘=’ , → , poser X
remplir blancs, ∀ , ☐ , ← , remplir blancsÉtat : poser X
# Après avoir trouvé le = ou déposé un chiffre, pose un x et part à la recherche du Y ou d’un chiffre.
poser X, ☐ , X , → , chercher Y
poser X, Y , X , → , prendreNombre
poser X, ∀ , ∀ , ← , retour sur égalÉtat : prendreNombre
# Si un chiffre est trouvé, entre dans l’état de déplacement qui lui correspond. Sinon, retour sur égal et stop.
prendreNombre, 0 , Y , ← , déplace0
prendreNombre, 1 , Y , ← , déplace1
prendreNombre, 2 , Y , ← , déplace2
prendreNombre, 3 , Y , ← , déplace3
prendreNombre, 4 , Y , ← , déplace4
prendreNombre, 5 , Y , ← , déplace5
prendreNombre, 6 , Y , ← , déplace6
prendreNombre, 7 , Y , ← , déplace7
prendreNombre, 8 , Y , ← , déplace8
prendreNombre, 9 , Y , ← , déplace9
prendreNombre, ∀ , ∀ , ← , retour sur égalÉtat : chercher Y
# Cherche le Y précédemment placé sur la bande. Si on trouve un chiffre à la place du Y, se placer dans l’état prendre Nombre sans bouger. Si on trouve le Y, le supprimer, aller à droite et aller à l’état prendre Nombre.
chercher Y, ☐ , ☐ , → , chercher Y
chercher Y, Y , ☐ , → , prendreNombre
chercher Y, 0 , 0 , prendreNombre
chercher Y, 1 , 1 , prendreNombre
chercher Y, 2 , 2 , prendreNombre
chercher Y, 3 , 3 , prendreNombre
chercher Y, 4 , 4 , prendreNombre
chercher Y, 5 , 5 , prendreNombre
chercher Y, 6 , 6 , prendreNombre
chercher Y, 7 , 7 , prendreNombre
chercher Y, 8 , 8 , prendreNombre
chercher Y, 9 , 9 , prendreNombreÉtat : retour sur égal
retour sur égal, ☐ , ☐ , ← , retour sur égal
retour sur égal, X , ☐ , ← , retour sur égal
retour sur égal, ‘=’ , ‘=’ , stop
retour sur égal, 0 , 0 , ← , retour sur égal
retour sur égal, 1 , 1 , ← , retour sur égal
retour sur égal, 2 , 2 , ← , retour sur égal
retour sur égal, 3 , 3 , ← , retour sur égal
retour sur égal, 4 , 4 , ← , retour sur égal
retour sur égal, 5 , 5 , ← , retour sur égal
retour sur égal, 6 , 6 , ← , retour sur égal
retour sur égal, 7 , 7 , ← , retour sur égal
retour sur égal, 8 , 8 , ← , retour sur égal
retour sur égal, 9 , 9 , ← , retour sur égalÉtat : déplace0
déplace0, ☐ , ☐ , ← , déplace0
déplace0, X , 0 , → , poser XÉtat : déplace1
déplace1, ☐ , ☐ , ← , déplace1
déplace1, X , 1 , → , poser XÉtat : déplace2
déplace2, ☐ , ☐ , ← , déplace2
déplace2, X , 2 , → , poser XÉtat : déplace3
déplace3, ☐ , ☐ , ← , déplace3
déplace3, X , 3 , → , poser XÉtat : déplace4
déplace4, ☐ , ☐ , ← , déplace4
déplace4, X , 4 , → , poser XÉtat : déplace5
déplace5, ☐ , ☐ , ← , déplace5
déplace5, X , 5 , → , poser XÉtat : déplace6
déplace6, ☐ , ☐ , ← , déplace6
déplace6, X , 6 , → , poser XÉtat : déplace7
déplace7, ☐ , ☐ , ← , déplace7
déplace7, X , 7 , → , poser XÉtat : déplace8
déplace8, ☐ , ☐ , ← , déplace8
déplace8, X , 8 , → , poser XÉtat : déplace9
déplace9, ☐ , ☐ , ← , déplace9
déplace9, X , 9 , → , poser X
