Le solveur 2.0 est plus performant que la version précédente. Parmi les nouveautés, la rotation des solutions permet de mieux comprendre le raisonnement suivi.

Rotation des  solutions

Des joueurs sur Actilud utilisent le solveur pas à pas pour apprendre à résoudre les intégrammes. C’est une très bonne idée. Mais il est quelquefois difficile de comprendre pourquoi le solveur a pris telle ou telle décision. C’est souvent parce que le solveur, même s’il fonctionne pas à pas, prend une foule de décisions d’un seul coup – et on a du mal à s’y retrouver ! C’est particulièrement vrai pour les techniques d’intersection, de répercussion ou de fusion.

Rappel du fonctionnement du solveur pas à pas

Lancer le solveur sur la grille de jeu.

Valider les modifications du solveur.

Annuler les modifications, d’abord le scintillement, puis toutes les couleurs.

Présentation de la rotation des solutions

La rotation des solutions se présente sous la forme d’une nouvelle icône dans la barre des outils. Lorsque l’on clique sur l’icône, la première solution apparaît; un nouveau clic fait apparaître la solution suivante, et ainsi de suite. Lorsque toutes les solutions ont été passées en revue, la rotation reprend avec la première solution, après une pause où aucune solution n’est affichée.

Notez qu’une solution s’appuie souvent sur les résultats d’une solution précédente- c’est aussi ce qui rend la compréhension difficile. L’ordre dans lequel vous passez en revue les solutions est donc très important; il reflète le raisonnement du solveur.

Les couleurs

Comme vous le savez sans doute, après l’utilisation du solveur pas à pas, si une technique est trouvée, les cases des grilles se colorent et les couleurs reflètent les changements opérés.

• le rouge indique un signe faux
• le vert désigne un signe vrai
• le jaune indique un changement concernant un booléen: nouveau booléen dans une case, ou remplacement d’un booléen par un autre.

Ces trois couleurs ne changent pas par rapport à la précédente version. Elles ne sont pas affectées non plus par la rotation des solutions.

Les bordures

Les solutions sont expliquées par les bordures.

Cette bordure désigne une case qui intervient dans une interaction; elle peut en être la cause ou ou la conséquence. En voici un exemple très simple.
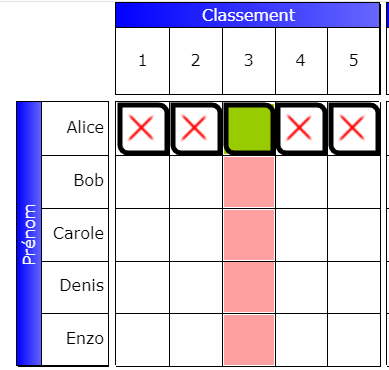Dans cette grille, la case en vert désigne une case vraie qui va apparaître suite à la technique du complément. La case apparaît parce qu’il y a 4 cases fausses sur la ligne. Les cases fausses, ici, sont les causes de l’interaction. La future case vraie en est la conséquence. Lorsque le solveur affiche la première solution, les conséquences font partie des cases colorées, alors que les causes ne sont souvent pas colorées. Mais attention ! Comme le solveur s’appuie sur les solutions précédentes pour découvrir de nouvelles solutions, ceci n’est plus vrai à la solution suivante ! De plus, il peut arriver que des solutions ultérieures modifient la couleur des cases de départ; donc les causes peuvent aussi être colorées.

Quand aux cases rouges, elles sont la suite logique de l’apparition de la case vraie. Mais là, le solveur n’indique rien. Son rôle a été de découvrir la case vraie. Ensuite, ce qui est trivial est ignoré pour ne pas surcharger les explications.

Case de référence. En général, cette case fait partie d’une alternative et contient donc un booléen. Les cases de référence permettent de comprendre les motivations du solveur. Ces cases, lorsqu’elles ne sont pas entourées par la bordure décrite ci-dessus, n’interviennent pas directement dans l’interaction, mais c’est parce qu’elles existent que l’interaction devient possible.

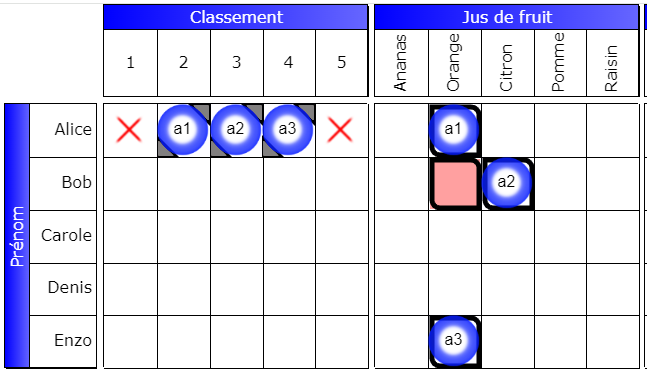
Ici, nous voyons que la case (Bob,Orange) est fausse, et nous comprenons que c’est à cause de l’interaction des trois booléens a1,a2 et a3. Cette case est à leur intersection. Mais pourquoi est-ce possible ? Voyez la ligne (Alice, classement) : les trois booléens a1, a2, a3 forment une alternative. Ces trois booléens-là, en (Alice,2), (Alice,3), (Alice,4),  n’interviennent pas directement dans la mise à faux de la case (Bob, Orange), car ce sont les booléens en (Alice,Orange), (Bob, Citron) et (Enzo,Orange) qui agissent. Mais elle l’explique : l’un des trois booléen de la ligne Alice est forcément vrai. Donc, quelque soit la valeur de a1, a2, a3 dans la grille (Prénom, Jus de fruit), Bob ne boit pas de jus d’orange.

L’encadrement de référence est utilisé dans l’implication et l’invariance. La case de référence subit l’hypothèse vraie et l’hypothèse fausse. Les autres cases sont la conséquence de ce test. Dans l’implication, si une conséquence est un booléen, il peut prendre la valeur de la case de référence. Comme la case de référence agit dans l’interaction, elle est aussi encadrée par la bordure d’interaction.

Case de référence qui intervient dans l’interaction. C’est un cas très fréquent.
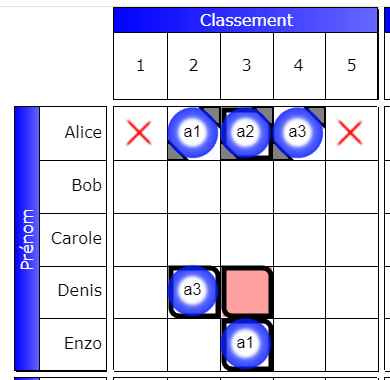L’alternative est formée par a1, a2, a3 (référence). Mais a2 intervient aussi directement dans l’interaction, ainsi que a3 de la ligne Denis et a1 de la ligne Enzo et bien sûr, la case fausse.

Pivot. Un pivot, c’est une case d’intersection entre deux rangées, que ce soit des lignes ou des colonnes. Ces rangées appartiennent à deux grilles différentes de celle où se trouve le pivot. Les pivots se retrouvent dans les techniques de répercussion et de fusion. Si le pivot est encadré, c’est qu’il intervient directement dans l’interaction, ce qui est le cas le plus fréquent.

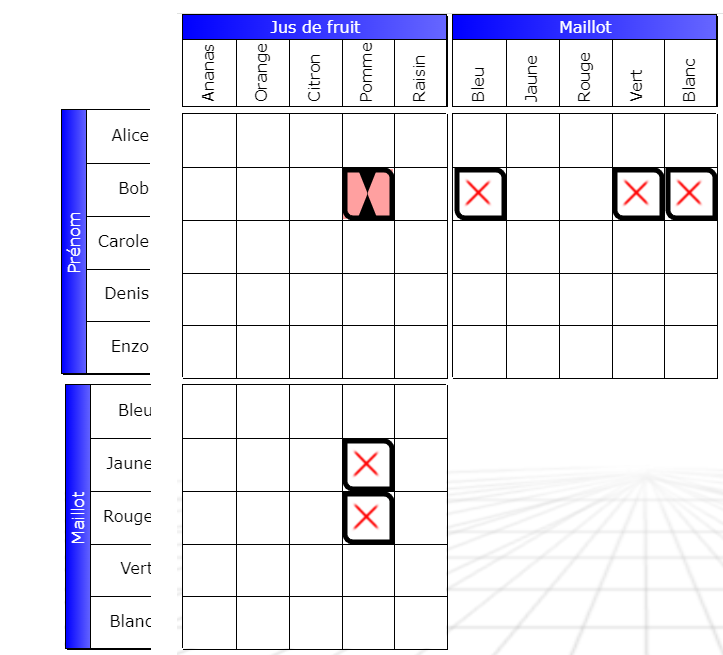
Bob ne boit pas de jus de pomme… parce que c’est impossible. Le pivot, résultat de l’intersection de la ligne (Bob, maillot) et de la colonne (Pomme, maillot), est forcément faux. On voit bien pourquoi grâce à l’encadrement des cases qui interagissent. Si Bob buvait du jus de pomme, il ne pourrait porter aucune couleur de maillot. La case pivot, ici, intervient aussi dans l’interaction, puisque son passage à faux en est la conséquence.

Booléen barré. Ceci n’apparaît que dans la grille des alternatives. Lorsqu’un booléen est barré, cela signifie qu’il peut être faux dans la grille du jeu, et qu’il est supprimé de la grille des alternatives.
Mais, dans la plupart des cas, cette marque concerne tous les booléens d’une alternative. Cela signifie qu’ils vont être retirés de la grille des alternatives car l’alternative qu’ils forment existe désormais dans la grille de jeu. Il n’est donc plus utile de la conserver dans la grille des alternatives.

Comme ce phénomène peut se produire à tout moment, il n’est pas spécifique à une technique donnée. Aussi peut-on retrouver des booléens barrés dans une technique qui, à priori, n’a rien à voir avec ceci. C’est juste le solveur qui signale qu’il a ôté les booléens de la grille des alternatives à ce moment.