Il est important que les élèves comprennent que quel que soit l’énoncé de type additif, il entre dans une seule modélisation, celle du modèle en barres classique :

Que l’on ait une addition ou une soustraction, c’est le même modèle qui sous-tend le problème.
Toutefois, comme tout modèle, le modèle en barres classique a ses limites. En particulier, il réduit toute soustraction à une addition à trou.
Certes, c’est vrai d’un point de vue mathématique.
Mais ce ne l’est pas dans la vie courante.
Lorsque j’ai 10 billes et que j’en perds 7, je ne fais pas une addition. Et je ne ressens certainement pas la perte comme un gain.
Même si je compte avec les doigts, je pars de 10, j’abaisse 7 et je compte ce qu’il reste. Alors qu’avec le modèle en barres classiques, je devrais partir de 7 et voir ce qu’il me manque pour arriver à 10. Ce n’est pas du tout le même raisonnement.
Répétons le, il est très important que les élèves comprennent que cette situation entre dans le cadre de la modélisation classique.
Mais d’un point de vue opérationnel, il m’a semblé pertinent de créer un nouveau modèle, la machine plus-moins, qui permet de mieux travailler la spécificité de la soustraction.
Si vos élèves sont suffisamment à l’aise avec le modèle classique, vous pouvez leur présenter le nouveau modèle. S’ils utilisent le site pour résoudre les problèmes, on peut même leur laisser le choix du modèle, selon leurs préférences ou, encore mieux, selon le problème du moment.
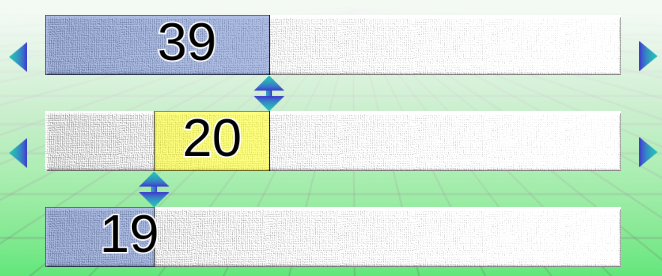
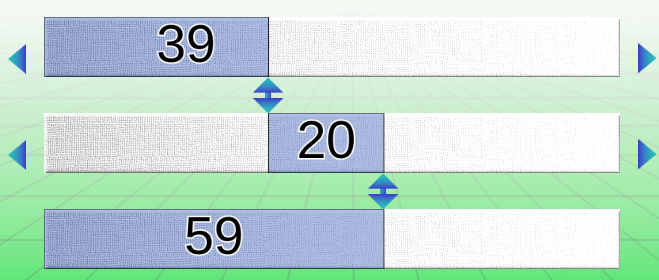
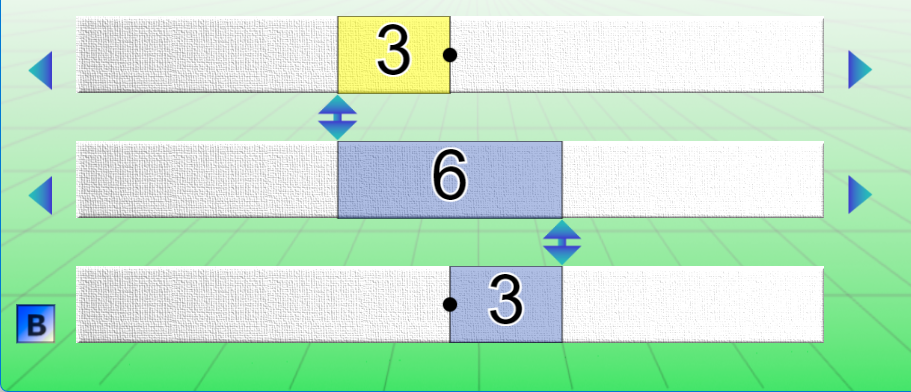
Les boutons A et B
Ces deux boutons situés en bas, à gauche de la machine, permettent de basculer entre deux modes de représentation.
Mode A
Il n’y a pas de partie négative; tous les nombres sont positifs et croissants à partir du bord gauche. Ce modèle est adapté à la plupart des problèmes de composition, transformation et comparaison.
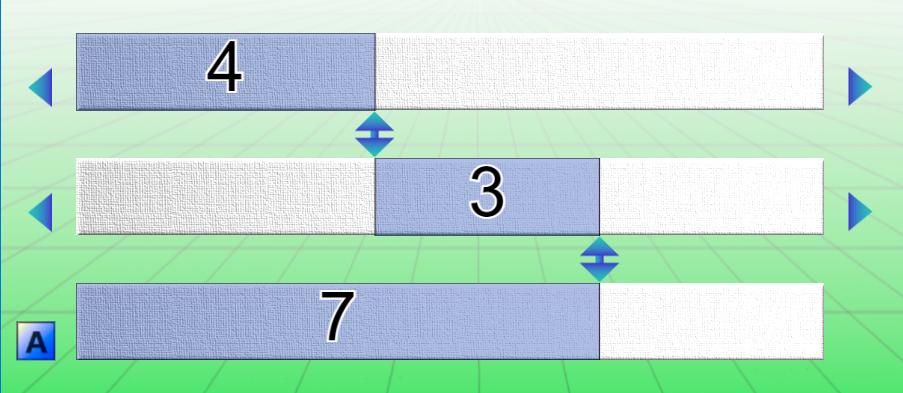
Mode B
Il y a une partie négative : la machine est « zéro centrée ». C’est utile dès que les élèves connaissent les nombres négatifs (il n’est pas nécessaire de les avoir abordés en classe ! Si vos élèves savent que la température peut chuter en dessous de 0 ils connaissent déjà les nombres négatifs). Dans le premier degré, cette représentation peut faciliter la résolution de problèmes de composition de transformations.
Conclusion
La machine « plus moins » est plus adaptée à certains problèmes de transformation et de composition de transformations. La machine classique est mieux adaptée aux problèmes de composition.
Attention, si vous vous lancez dans l’utilisation de ce modèle, sachez qu’il n’est pas documenté ! C’est une invention de ma part pour Actilud. Cette machine demande des moyens modernes pour fonctionner- un ordinateur, une tablette… dispositifs largement ignorés dans la didactique des maths, et donc à ma connaissance personne ne l’a imaginée.
Donc, soyez moderne, utilisez la machine « plus moins ». Avec prudence et discernement. Mais essayez la ! Vous verrez qu’elle est très intéressante aussi.
