Numbers are hidden and form a circuit. Each number is separated from the next by an operation. To find the numbers, all the operations must match.

The basic rules

Numbers are all natural integers between 1 and 100. This rule is fundamental! It allows you to frame your search.

We use the four basic operations: addition (+), subtraction (-), multiplication (x) and division (:).

According to the rule, subtraction must produce a natural number greater than 0. So, in the operation a – b , we must have a > b .

Division is Euclidean division without remainder. In other words, for the division a : b to be possible , b must be a divisor of  a.

8:2 ok
8:3 impossible
8:4 ok
8:5 impossible

The circuit is reversible. Simply change the direction of the arrows. The “+” then swaps with the “-“, the “x” swaps with the “:”.

To change direction, click on the double arrow in the center of the circuit.

Of course, the circuits offered on Actilud only have one solution, as long as the numbers are within the imposed limits.

The operators

An operator is the number that appears after the operation.

In addition and subtraction, the operator will always be between 1 and 10.

Multipliers and divisors range from 2 to 12.

The strategy

The first strategy is to write the equation corresponding to the circuit and solve it! This is a very interesting exercise in middle school, but of course it is not on the elementary school curriculum. For example, the equation of the circuit below (example 1) is:

a = 9 (a-2) / 6

which resolves to: a=6

a is the number in box A

Transforming a circuit into a formula is not easy! Operator precedence must be respected to write the operations in the correct order.

The other strategy is “brute force”: try all the numbers one after the other in a box, propagating them, until you get a consistent result! Obviously, while this strategy is fairly simple to program on a computer, it is hardly satisfactory for a human. It will probably be favored at the beginning by students, especially if we allow the calculation of operations by computer.

So let’s look at some ways to improve performance; our goal is to develop a sense of operations!

Definition: a, b, c, … are the numbers placed respectively in boxes A, B, C, …

Find the location of the smallest number

This clue allows us to target a starting square for our calculations. To do this, we must ask ourselves which operations in our circuit decrease a number. It’s easy: it’s subtraction and division. Within the framework of the rules explained above, as soon as a number is greater than 20, division decreases the number more than subtraction; we will therefore favor it, except in exceptional cases. When several successive operations are divisions and/or subtractions, we can be fairly certain that the arrival square of the series contains the smallest number.

Caution: associating division with decrease is true in the set of positive natural numbers, if the divisor is greater than 1. But this is not the case with real or decimal divisors between 0 and 1: 20 / 0.5 = 40.

In a three-step puzzle, it is often quite easy to find the box containing the smallest number:

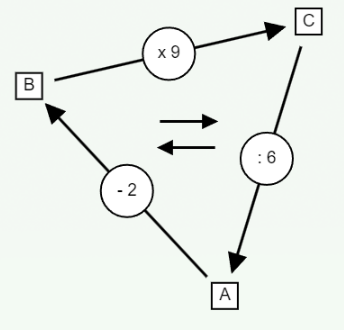
Here there are two successive operations of decrease: (: 6) and (- 2). For sure, box B contains the smallest number. A priori, the minimum value of b is 1 and its maximum value is 11, because it is followed by a multiplication by 9 whose result must not exceed 100: b ∈ [ 1 , 11 ]. This allows us to deduce the values ​​of c and to write them by extension: c ∈ { 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99 }.  We can then use the technique described below to finally discover that C must be a multiple of both 9 and 6, which gives: c ∈ { 18, 36, 54, 72, 90}. There are only 5 more possibilities to test.

Find the box that is a multiple of the two neighboring boxes.

When a multiplication is followed by a division, the box at the intersection of the two operations must contain a multiple that is suitable for both operations.

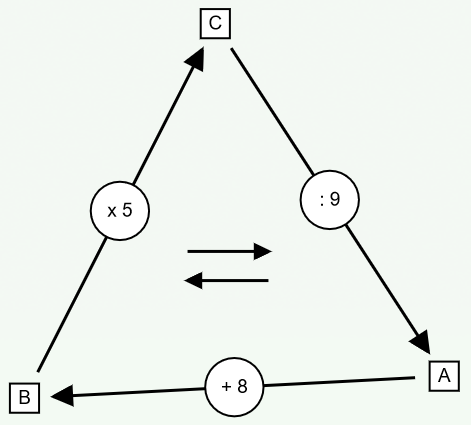
Box C must be a multiple of 5 but also divisible by 9. We must therefore find the multiples common to 5 and 9; there are only two possible between 1 and 100: 45 and 90. We therefore only have two tests to perform!

Note: this technique does not apply to the opposite case – a division followed by a multiplication.

Observe the circuit carefully and look for a general law

Still within the technique of multiplication followed by division, we can sometimes limit the number of possibilities by carefully examining the circuit. In the case below, we see that box F contains multiples of 10:

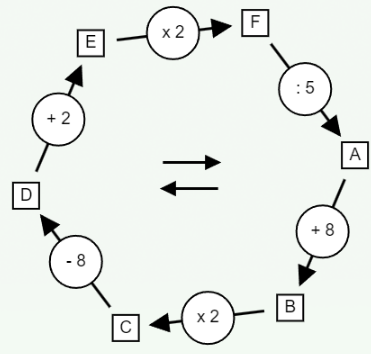
But let’s take a good look at the path that leads to square F. Let’s start from B. The number in B is multiplied by 2, which gives an even number in C. Then we subtract 8, but doing so still gives an even number. Then we add 2, which still gives an even number. Finally, this even number is multiplied by 2. Now, an even number multiplied by 2 gives a multiple of 4! So, the square in F contains a multiple of 20, which leaves only 5 cases to examine, instead of 10: f  ∈ { 20 , 40, 60 ,80, 100 }

Multiple arrivals or departures

If in a circuit, a box is at the arrival of several consecutive multiplications, it contains a multiple of these operations.

If in a circuit, a box is the starting point of several consecutive divisions, it contains a multiple of these operations.

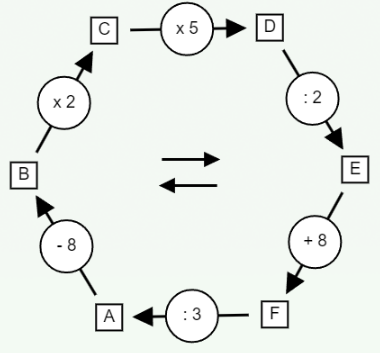
In the example above, box D is at the end of two multiplications, x2 and x5: it therefore contains a multiple of 10.

Note also that box E contains a multiple of 5! Indeed, to arrive at E from B, multiplication and division by 2 cancel each other out.

The meaning of operations

The word “meaning” has a… double meaning! On the one hand, it refers to the reversibility of the operation (A x B  ⇔ B : A), and on the other hand, it refers to the understanding of the operation.

In the example above, we see that we often reverse the calculations: in example 1, to get to box A from C, we do a division. But to find C from A, we do a multiplication.

To properly master the operations, it is therefore necessary to use reversibility.

But that’s not enough. You also need to understand and use the concepts of divisor and multiple . If you can recognize a multiple or a divisor at a glance, you can avoid a lot of calculations. Knowledge of the multiplication tables is very important here.

A simple way to introduce the concepts of divisors and multiples is to use something students already know: multiplication tables. Simply point out that any multiplication can be written in the form: divisor1 x divisor2 = multiple.

It is imperative to use a support to write down hypotheses; otherwise, one risks fumbling around without much efficiency. It saves time if one writes intervals for consecutive numbers, or extensive sets of possible numbers to be crossed off as one goes along.

When the grids have more than 3 squares, it is more difficult, but we can proceed in the same way, step by step.

From automatic operations to mental calculation

By default, after dropping a label on a box, you can click on the corresponding operation. This is automatically performed and the result, a new label, is placed in the next box. If there was already a different label in this box, it is moved to the side, which allows you to keep track of it.

Automatic operations allow students to focus on the essentials, discovering a strategy without being distracted by calculations. I recommend this approach at the very beginning. It allows everyone to clearly understand what’s happening, thanks to the label animations. You can also flip the arrows; the action is visual and clearly shows that the direction of the operations changes, and that the operations themselves are permuted.

Of course, automatic operations are crutches that, in the long run, risk reducing the effectiveness of research! Secondly, we can inhibit automatic operations, while retaining the possibility of performing calculations with the calculator – which is already more tedious and encourages students to mentally calculate simple operations.

Finally, once the students are trained, we prohibit any help (apart from the rough draft, of course), to encourage mental calculation.

In any case, it is advisable to bring a rough notebook. Alternatively, you can use the notepad provided for this purpose.

Mental arithmetic can be learned!

Just in case, here’s a helpful reminder of what students should know.

Know addition and multiplication tables well.

This is obvious. Without it, no effective mental arithmetic is possible. The game is also a good way to practice if you remove the automatic help.
It is recommended that students also know the table for 11 to 99 (which is easy) and the table for 12 (not so easy but so useful).

Know how to identify divisibility

Here is a quick reminder of techniques which, while not universal, are applicable to numbers up to 100.

divisible by 2: the number must be even (universal rule.)

Divisible by 3 : Add up all the digits in the number. The digits 9 can be replaced by 0. If the result is a multi-digit number, repeat the operation on the result until you get a single digit. In the end, the number obtained must be 0, 3, 6, or 9, i.e., a multiple of 3 (universal rule).

124932:
1 + 2 = 3
3 + 4 = 7
7 + 9 ⇔ 7 + 0 = 7
7 + 3 = 10, 1 + 0 = 1
1 + 2 = 3
124932 is a multiple of 3

divisible by 4 : the last two digits form a number which is itself divisible by 4. As we only learn the 4 times table up to 40, we can subtract 40 or 80 from the number formed by the last two digits if it is too large, before checking divisibility by 4 (universal rule).

Is 2576 divisible by 4?
76 – 40 = 36
36 is divisible by 4 => 2576 is divisible by 4

divisible by 5: the number ends in 0 or 5 (universal rule).

divisible by 6: the number must be even and divisible by 3 (universal rule)

Divisible by 7: The number must be in the 7 times table. If it is greater than 70, first subtract 70.
There is a universal technique, little known, which is not generally taught because it is too complex. We remove the last digit of the number, double it, and subtract it from the truncated number. We repeat this process as many times as possible. At the end, we check whether the result is in the 7 times table.

Is 2401 divisible by 7?
We remove the 1, we have 240 left
240 – (1×2) = 240-2 = 238
We remove the 8, we have 23 left
23 – (8×2) = 23 – 16 = 7 present in the 7 table
2401 is divisible by 7

divisible by 8: no special technique; if the number is odd, it is not divisible by 8. If it is even, it must appear in the 8 times table. Subtract 80 if it is greater.

divisible by 9:  use the rule of divisibility by 3. If the result is 0 or 9, the number is divisible by 9 (universal rule).

divisible by 10: the number ends with a 0 (universal rule).

divisible by 11: the number (smaller than 100!) is formed from two identical digits: 11, 22, 33, 44, etc.

divisible by 12: no special technique; check if the number is even. If it is, check that it appears in the 12 times table.