B- CODING

The designer is a powerful engine that is used on Actilud in the puzzles “Jogging”, “Kite”, “Fashion Show”, “Sand Yacht”, “Orchard” . It allows you to create random, different puzzles of varying difficulty, depending on the programming.

It therefore needs to be programmed with the instructions present in the left-hand selector, which offers 9 instructions.

Once programmed, the designer executes the instructions and generates a puzzle in the form of formal statements. This riddle is already playable, but to be readable by everyone, the formal statements still need to be translated into a text that everyone can understand.

To enter the coding part, click on the Menu icon in the toolbar and, in the dialog window that opens, choose the Code button.

The following window appears:

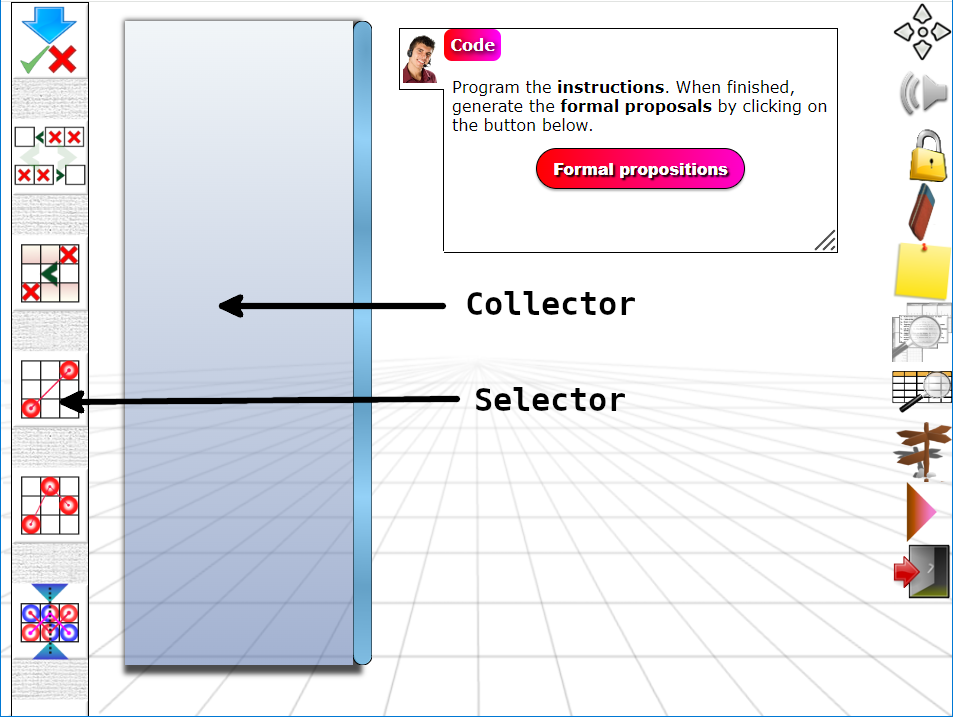
The collector contains and organizes the instructions drawn from the selector. Instructions can be moved within the collector to organize them as desired.

To instantiate an instruction, go to its icon in the selector, click or point and hold; the instruction appears. Simply drag it into the collector. Only instructions present in the collector will be taken into account during execution.

A minimum program

Let’s get started! We’re going to create a minimal program consisting of a single instruction that will generate a complete puzzle.

The data in the zebra puzzle is that of the predefined example : runners arrive in a specific order, wear a different colored jersey and each drink a different fruit juice at the finish.

When starting the program: button  use a predefined example;

Or click the menu icon in the toolbar, design, use a pre-defined example button  .

We’ll use the PLACE instruction:

The PLACE instruction icon is the first in the list. Expanded instructions appear as a strip.

When you click on the pencil , the advisor displays a description of the instruction and allows you to configure it. The changes are reflected in the display as soon as you confirm the entry .

As the name suggests, the instruction will place a true or false sign in a randomly chosen empty and suitable location on the grids.

Random choice

We will let the program itself choose whether to place a true sign or a false sign. To do this, in the Sign choice field, we choose random.

If we validate at this stage, the strip changes appearance:

Number of repetitions

We wouldn’t be very far ahead if our designer simply displayed a single symbol. Our example puzzle has six 5×5 grids, or 150 squares. Therefore, all 150 squares must be filled by the designer’s end. This is the role of the Maximum field. So, let’s change the maximum number of repetitions.

This is a maximum, but it won’t necessarily be reached. For my part, when I want to loop through an instruction to the end, I type 1000, regardless of the size of the grids.

So type 1000 in the Maximum field and validate.

As you can see, the change is reflected immediately after validation.

If the maximum is too low, the designer will multiply creation attempts but will never succeed in creating a complete puzzle. It is then necessary to interrupt the execution and modify the program.

Looking for solitude?

If you check the Isolated box, the randomly chosen boxes will be at an intersection where the row and column are completely empty: no false sign, no Boolean and obviously no true sign . Checking isolated can be useful if you want to make the puzzle a little more interesting but the calculation time will be increased.

In some cases, using isolated makes computations impossible; this is the case here if you set  Sign Choice  to false and  isolated  to true. With this single instruction set like this, the solver will never be able to create a puzzle.

Execution !

Click the advisor’s formal proposals button . If it doesn’t appear, click the pencil icon for the instruction you’re currently editing in the collector.

The advisor offers two difficulty levels. Leave the standard level. Check that the Maximum number of attempts before retrying field contains 10,000 (ten thousand) and confirm. After a few seconds of work, the result should appear:

 

Here is a list of formal propositions. They are already usable by the solver.

This is my list! Yours is bound to be different, since this is all random!

Use the Autocomplete button then click on a statement to make it appear in the grid.

Text explanation

But what does the line mean:

White ∩ Grape= True

The intersection of the white row and the grape column contains a true sign .

Furthermore, there is no possibility of confusion. If there is ever a risk of confusion with two identical items (such as the orange color of a jersey, which can be confused with orange juice), the designer will systematically indicate the corresponding heading:

Orange Jersey ∩ Orange Fruit Juice = False

Bis repetita placent

What does the Maximum number of attempts before  advisor restart field mean, in which we set the value to 10000?

The designer operates recursively. It may occasionally stumble into a dead-end calculation. The number specified is the maximum number of evaluations that a configuration is allowed to run before the designer restarts the program—it tries again.

This can be seen when the attempts counter increases.

If you set the value too low, the designer will not have the opportunity to make all the necessary evaluations to find a viable puzzle.

So, if you see the number of attempts increasing too quickly, it means the number of evaluations allocated is too low. Stop the process and increase the value.

Conversely, if the value is too high, the designer may get lost in his calculations. Reduce the value.

It all depends on the program, of course.

For our simple program, the value of 10000 is perfect because it requires a lot of evaluations, but the risk of going astray is low. But for a more complex program, we will probably need to lower this value. Often, the value 1000 is a good compromise for more sophisticated programs.

So the maximum number of attempts allows the designer to be set.

• we decrease the value if the calculations are too long;
• we increase the value if the number of attempts explodes!

Standard or expert?

At the moment, the editor only offers two operating choices: standard or expert .

Standard mode

Suitable for simple puzzles.

• instructions showing true signs are preferred;
• advanced techniques, such as invariance or implication searching, are not used.

For a given program, the puzzles produced will be quite short.

Expert mode

Suitable for difficult puzzles. Longer puzzles are generally produced.

• the designer tries to maintain the booleans as long as possible: quick solutions are therefore rejected;
• advanced resolution techniques are performed;
• The puzzle must be solved with at least one appeal to one of these advanced techniques; otherwise it is rejected as “too simple.”

In our example, using expert mode is possible if we only place false  signs ; but you generally have to wait quite a long time: advanced resolution techniques are not very available because here, our programming (a single, very simple instruction that we repeat) is basic. In expert mode , the designer multiplies the attempts and rejects those considered too easy. But if you wait enough, he will eventually find a solution… which will take a very long time.

A simple program for ages 8 and up

With a little help and explanations, an 8-year-old should be able to do this. The educational value, besides coding, is mainly to encourage them to write logic statements.

Our new program contains two instructions: the PLACE instruction, which we just saw, and the next instruction, THRESHOLD.

The THRESHOLD instruction must be placed first.

Since we are using the predefined example, this instruction will only apply to the Ranking series, which is the only one with an order relationship.

What does the THRESHOLD instruction do? It introduces a limit into a series, for a given item. Here’s an example:

Alice arrived before the 3rd.

This proposition places three false signs, at the intersection of Alice and 3rd, fourth and fifth.

Recommended settings:

THRESHOLD :

• isolated: true
• maximum number of repetitions: 10

PLACE:

• choice of sign: random
• isolated: false
• maximum number of repetitions: 1000

In fact, since we’re asking for isolation for THRESHOLD, there will never be 10 repetitions. But it doesn’t matter if this maximum is never reached; what we want is to get a large number of formal proposals for this instruction.

Here is what our program looks like before it is executed:

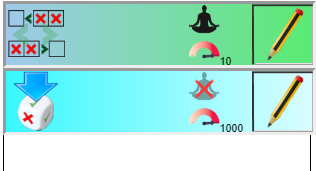
To terminate a program, it is recommended to include a “fill the holes” instruction. Here we use “random” PLACE, but in more sophisticated programs, a “false” PLACE repeated 1000 times is recommended.

The settings are standard and the maximum number of attempts is 10000.

We should obtain a formal statement with about fifteen propositions, like the example below.

Grape < 3

The person drinking grape juice came in before third place.

How does the designer work?

If you’re curious, here’s how it works.

Let’s say a program consists of a series P=(i ₁ , i ₂ , i ₃ , …. i _n ) of elementary instructions. An elementary instruction is one that is executed only once. When an instruction is repeated n times by the program, this means that there are n elementary instructions in a row that will be executed.

Each instruction, when executed, produces one occurrence drawn at random from all those possible. For example, for the instruction PLACE false, there are roughly 150 possible occurrences, since there are 150 boxes in our grid (in fact there are fewer, since there are calculated inferences: when we place a “true” sign, there are automatically 8 false boxes).

The designer throws an occurrence of i ₁. If it succeeds, he throws an occurrence of  i ₂ , then i ₃ , and so on. If, on reaching the occurrence i _p, there is a failure (impossible to solve the puzzle because of contradictions), the designer tries another occurrence of i _p, chosen from all those still available. If none succeeds, the designer keeps the series(i1, i2, … i _p-2 ) and calculates a new occurrence of i _p-1(since “under” the previous occurrencei _p-1  no ip passes), then continues with i _p .

This is why some calculations can take an enormous amount of time. In this case, you need to limit the number of evaluations. As chance has a way of doing things, we always end up finding an acceptable solution by re-trying new calculations from the beginning, rather than struggling to finish titanic calculations that could take millennia.