by In the Numbers and Operations section, you will find an assortment of abacuses available for free work, group use, or individual exercises.
The counting abacus
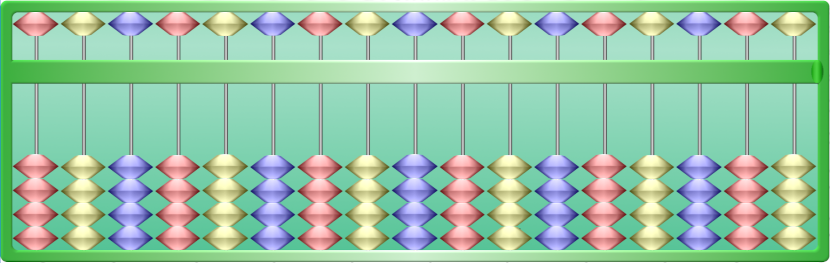
The counting abacus on Actilud uses the same codes as a traditional children’s abacus. It consists of 10 rows of ten tokens, each token worth one unit. There is no positional logic: the value of the token does not vary according to its row.
On Actilud, the lines have a variety of colors—which children generally like—but each line is divided into two parts of 5 tokens, which are easily distinguishable because they use complementary colors. This makes it easier to overcount from 5.
Each abacus generates its own colors, which are never the same from one instance to another.
To use the counting abacus, slide one or more tokens from one side to the other. The direction of movement depends on the model chosen. In the settings menu, you can choose a direction of movement from left to right, or vice versa. The most recommended direction is moving the tokens from left to right, as this is the common direction of writing in our societies. However, Actilud also provides a direction from right to left.
As the name suggests, the counting abacus is useful for students who still need to count to succeed in a calculation.
The advantage is that you can easily write the tens by moving a row of 10 beads in one go. To move from left to right, you activate the leftmost bead and move it to the right, which will push the others.
Understanding decimal decomposition is therefore greatly facilitated: if I have to write 38, I slip in three tens and then another line of 8 beads, thus performing the decomposition into tens: 38 = 10 + 10 + 10 + 8. The number 8 can itself be decomposed by taking 5 tokens of the same color on a line and adding the missing 3. The student is thus invited to move from a logic of counting units to a logic of grouping by tens and overcounting.
This abacus is suitable for operations on whole numbers less than or equal to 100. The sum does not exceed 100.
In free practice, the notepad allows you to visualize the numbers throughout the exercises. The software adds up all the tokens on the right (or left depending on the model chosen), regardless of the distribution of the tokens on the abacus.
The Suanpan, or Chinese abacus
The Suanpan is a positional logic abacus. The columns are arranged from right to left, from the lowest weight on the right to the highest on the left, exactly as numbers are represented.
So the units are on the right, followed by the tens in the rod immediately to the left, then there are the hundreds and so on.
Each column is organized with reference to the anatomy of the hand. The top two quinary tokens correspond to the two hands. The bottom unary tokens correspond to the five fingers of the hand.
The value of the tokens is multiplied by a factor of 10 when moving from one column to another.
To write a number, we move the tokens closer to the horizontal bar that crosses the abacus – the reckoning bar. We therefore move the quinary tokens down and the unary tokens up.
Here is one way to write the number 15,375:
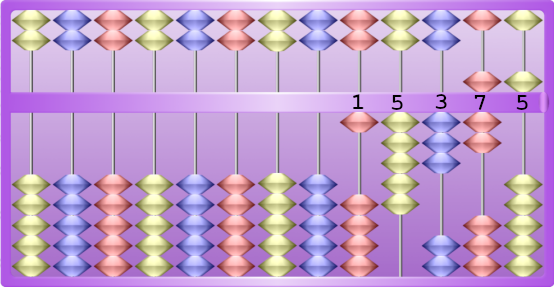
Note that in the number illustrated above there are two ways to write the digit 5: either with 5 tokens in the bottom column, or with a quinary token in the top column. Preference should be given to the most compact writing possible, namely a quinary token rather than 5 unary tokens.
There are three ways to write the ten; again, the most compact is preferred.
- one quinary token and 5 unit tokens,
- two quinary tokens,
- an unary token in the upper ten, which is the best solution.
The trick is to transform the unary tokens into either quinary tokens or higher-weight unary tokens. To transform 5 unary tokens into one quinary token, a skilled manipulator will make a single gesture with the thumb and index finger, to lower a quinary token and, at the same time, lower the 5 unary tokens. On Actilud, since “multi-touch” is not programmed, this must be done in two steps.
The rule is therefore simple:
- 5 unary tokens transform into one quinary token
- two quinary tokens, or ten unary tokens, transform into one unary token of the higher ten (left column)
This way, by successively reducing the tokens, we can perform complex calculations. On Actilud, we offer addition and subtraction. But we can also try multiplication or division, as free work.
The decimal separator
This is an educational exclusive available only on Actilud! The decimal separator (ofen a point or a comma) is the small tab, initially on the right of the reckoning bar, which can be moved along the axis; it indicates the start of the decimal part. Try it out in free practice with the notepad. This allows you to use the abacus with decimal numbers.
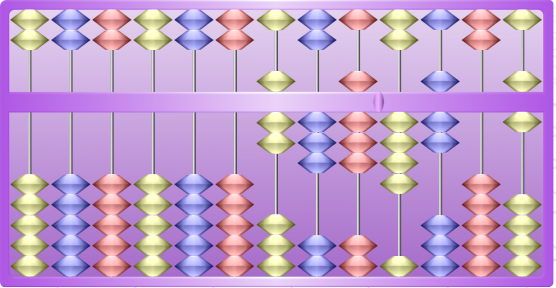
On Actilud, the Suanpan is available in 4 different sizes: 13, 10, 7, and 4 rods. Since we group numbers into sets of three digits, the columns are colored in three colors: yellow, red, and blue. The color to the left of the tab defines the units (yellow by default if the tab is on the right), then the tens (red), then the hundreds (blue). Then, we start again with the same color for the thousand units, tens of thousands, hundreds of thousands, and so on. In the illustration above, the units are in red because the tab has been moved.
The Soroban and the Roman abacus
The Soroban, or Japanese abacus, is the simplified version of the Suanpan. Here, there is only one quinary token per column, and 4 unary tokens instead of 5. This allows only one writing for each number. Thus, a ten can only be written using a single unary token that is moved up in the upper tens column, unlike what happens with the Suanpan.
As a result, the calculations are a little less natural, since it is no longer possible to make reductions, as one could do with fingers and hands. Reductions must be anticipated.
Our Soroban also has, as an educational exclusive, its decimal separator, which works on the same principle as that of the Suanpan.
The use of the Soroban will be reserved for students who already know how to calculate, to arouse their curiosity and develop their mental agility.
It is a very efficient calculation technique and was used a long time ago by the Romans.
A little tour in Roman antiquity
Actilud also offers a simulation of Roman abacuses, still in the numeration section. These abacuses work on the principle of the Soroban. For those who are interested, I made a video that explains in detail the calculation methods to use. This video explains the operation of the Roman educational abacus, which is nothing other than a Soroban with 4 columns ( see the video -in french for now).
The video specifically explains how to handle quinary and decimal passages. In the game menu, there is an entry that allows you to practice quinary or decimal passages.
Finally, the curious will find in the game a reproduction of two Roman abacuses, in ivory and bronze, usable without constraint: if you teach fractions, you will undoubtedly enjoy calculating ounces, semunciae and other duellae, as our ancestors did.
The Stchioty
The Stchioty, or Stchoty, is the Russian abacus. Actilud offers it in two main variations: with 10 or 9 tokens per line, and 4 orientations! depending on whether you want to use it in the European, Russian, Arabic, or personal way! Of course, I adapted it a little. Ours does not have a 4-beads rod, which was used in the past (not so long ago… until 1990) to calculate quarter Kopek. It also gained its decimal separator. The starting position of the separator allows you to identify the “units” row.
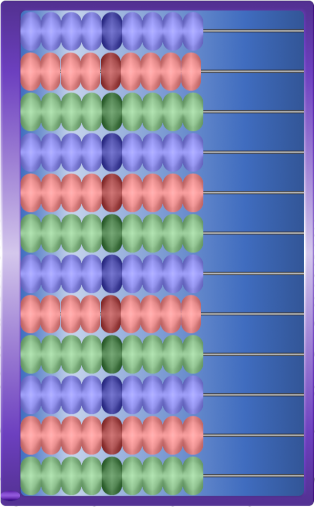
The Stchioty is like the counting abacus, but with positional algebra. So there’s a “units” row, a “tens” row, a “hundreds” row, and so on.
Each token has the value of its row, always multiples of 10.
The central tokens are accented to clearly distinguish the quinary values.
The 10-tokens abacus allows reductions: when the value 10 is reached, all ten tokens are returned to their starting position and a token of the higher ten is lowered. The operation is then reminiscent of the Suanpan without the quinary.
The 9-tokens abacus works more like a Soroban, without the quinary tokens of course.
In a pedagogical progression, the Stchioty is quite suitable as a successor to the counting abacus.
Exercises: working with integers or decimals
In addition to free work, the exercises allow you to :
- represent integers or decimals on abacuses
- add integers or decimals on the abacuses
- subtract integers or decimals on the abacuses
The numbers are of course limited in size by the capacity of the chosen abacuses. If it is considered too large, it can be further reduced; it is possible to limit the maximum to 100 on all abacuses, and to 1000 on all except the counting abacus. On large abacuses, the largest number will be 10 12 -1.
The maximum number of decimal places is also configurable, between 1 and 6.
It should be noted that using the abacus with decimals requires the correct positioning of the decimal separator. For example, in the following case: 14.5 + 13.58 the student must realize, when writing the first number, that he must leave two decimal places and not one, otherwise he will not be able to write the second. Of course, the software warns him if he makes the mistake. In operations, the software does not always put the same number of decimals to the operands! This is what makes the exercise all the more interesting.
The other advantage of using abacuses with decimal numbers is that it is the position of the decimal separator that determines the position of the unit. I think that in understanding decimal numbers, the fact that we can write the same decimal number in several places on the abacus, depending on the position of the decimal point, is a determining factor.
The software takes this into account and accepts all valid configurations, as long as the numbers are correctly written and the calculations are feasible.
To learn how to add or subtract, you can take a look at the video on Roman abacuses. It only covers the Soroban, but adapting it to other abacuses is fairly easy.
Progress of an operation
First, the software indicates the operation that will be performed; it is an addition or a subtraction, depending on the settings. At this stage, you are asked to enter the first number. This is essential to ensure that the operation will be performed correctly on the abacus.
Once the number is entered, the student must validate it. If the number is correct, we move on to the next step; if not, we must start again, but the student then benefits from the help of the notepad, which indicates the value of the abacus.
The second step is to perform the calculation. Here, the eraser doesn’t erase the abacus, but replaces the original number. This is useful in case of hesitation, if you want to start again.
After the first mistake, the notebook becomes accessible; the pupil can then see the result. This doesn’t help much at the moment, since the goal is precisely to calculate it. But the pupil can always try to do a mental calculation.
After a second error, the calculator becomes accessible. The pupil can then try to use it… if the requested number fits on the calculator! The calculator only offers 8 digits… So, mission impossible as soon as we encounter a whole number of one hundred million or more, or a decimal with many places after the decimal point. In passing, we discover the power of these abacuses, capable of surpassing the size and precision of the numbers on our calculators.
But this difficulty is not a real problem, because the very large numbers are only proposed – obviously – if the pupils are already able to perform calculations on more accessible numbers. Letting them handle very large numbers is then an excellent opportunity to surpass themselves, a challenge, which some will appreciate.
Link to the Roman abacus video . (french)
Links to the games:
