Adding sticks
Stick arithmetic is probably the easiest to implement with a Turing machine. The collection to use is C={ ☐, |, X, =, +}.
We write an addition on the strip with sticks, for example: ||||+||=
The result should be of the form: ||||+||=||||||
Start on the = sign or on the stick immediately to the right, as you wish. End on the first blank to the right of the answer.
Description
The head first goes to the left. If it encounters an X, the + sign, or the = sign, it continues left. If it encounters a stick, it transforms it into an X and moves right until it encounters a blank. There, it writes an X and begins moving left again. If it encounters a blank while going left, it returns to the right, transforming all the Xs into sticks, and stops at the first blank.
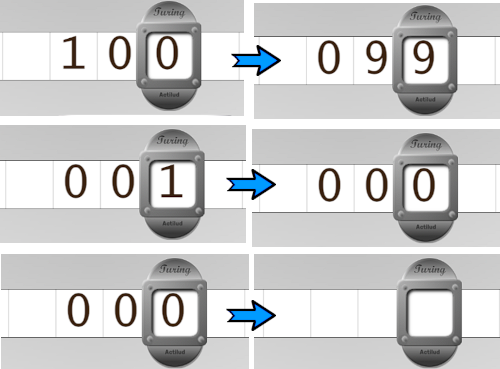
Universal decrement of a natural number
We often need to evaluate the value of a number, and the easiest way to do this with the Turing machine is to decrement the number. We are going to create a Turing machine that can be reused in larger programs. This involves decrementing a natural number placed on the tape by one digit per square. If the integer reaches its final value, 0, then the 0 must be erased; if there are several consecutive 0s remaining, they must all be erased. The program must stop on the last digit, or on the last blank it has written if it has erased everything. Why? Because another program that uses our machine must “know” whether the machine has performed a decrement or not. As long as it stops on a digit, it means that the decrement has taken place. If it stops on a blank, it means that the decrement is complete. This is how our machine passes the information to the calling machine.
Our machine must also allow for the possibility that there may be signs other than blanks on either side of the number. We therefore prefer to use the sign ∀ to identify any sign other than the digits.
Here are some examples; the position of the head indicates the starting point and the ending point.
Solution: The Decrement Machine (spoiler)
Machine: [Decrementer]
# Decrements a natural number. If there are any remaining 0s, replace them with blanks. Always stops on the last digit, or the blank.
# Start: on the rightmost data item
# End: on the rightmost data itemState: Decrement
Decrement, 9 , 8 , → , transitRight
Decrement, 8 , 7 , → , transitRight
Decrement, 7 , 6 , → , transitRight
Decrement, 6 , 5 , → , transitRight
Decrement, 5 , 4 , → , transitRight
Decrement, 4 , 3 , → , transitRight
Decrement, 3 , 2 , → , transitRight
Decrement, 2 , 1 , → , transitRight
Decrement, 1 , 0 , → , transitRight
Decrement, 0 , 9 , ← , Decrement
Decrement, ∀ , ∀ , → , erase9State: transitRight
# Skips all digits up to the last digit. Stops on the last digit.
transitRight, 9 , 9 , → , transitRight
transitRight, 8 , 8 , → , transitRight
transitRight, 7 , 7 , → , transitRight
transitRight, 6 , 6 , → , transitRight
transitRight, 5 , 5 , → , transitRight
transitRight, 4 , 4 , → , transitRight
transitRight, 3 , 3 , → , transitRight
transitRight, 2 , 2 , → , transitRight
transitRight, 1 , 1 , → , transitRight
transitRight, 0 , 0 , → , transitRight
transitRight, ∀ , ∀ , ← , stopState: erase9
# Erases all consecutive 9s; stops on the last blank.
erase9, 9 , ☐ , → , erase9
erase9, ∀ , ∀ , ← , stop
Place N apples!
In some cases, you need a large number of objects on the tape to test a program. For example, you would need 100 apples to check whether a counting program goes from 1 to 100. Of course, if you have time to waste, you can manually place the apples one by one on the tape and test the program.
But we can also create a Turing program! We write a natural number greater than 0 on the tape, the head is placed on the last digit.
And here is the final situation: the head stops on the first apple in a series. The number originally written on the strip is erased. The apples are placed to the right of the initial number.
![]()
Convenient, isn’t it? To run the program, once the debugging phase has been completed, we recommend using the fastest operating mode – the “horse to finish” button, for example. Execution time increases rapidly with the number of apples.
c= {[0-9],☐,apple}
Solution 1: Everything in the same machine (spoiler).
Machine: [Repeater]
# Decrements a natural number and places that many apples to the right of that number.
State: Decrement
# Decrements a number
Decrement, 9 , 8 , → , TransitRight
Decrement, 8 , 7 , → , TransitRight
Decrement, 7 , 6 , → , TransitRight
Decrement, 6 , 5 , → , TransitRight
Decrement, 5 , 4 , → , TransitRight
Decrement, 4 , 3 , → , TransitRight
Decrement, 3 , 2 , → , TransitRight
Decrement, 2 , 1 , → , TransitRight
Decrement, 1 , 0 , → , TransitRight
Decrement, 0 , 9 , ← , Decrement
Decrement, ☐ , ☐ , → , Delete9
State: Delete9
# Deletes all 9s and stop.
Delete9, 9 , ☐ , → , Delete9
State: TransitRight
TransitRight, ☐ , apple , ← , TransitLeft
TransitRight, ∀ , ∀ , → , TransitRight
State: TransitLeft
TransitLeft, apple , apple , ← , TransitLeft
TransitLeft, ∀ , ∀ , Decrement
Solution 2: two machines, the one that decrements is a repeat of the previous exercise (spoiler)
Machine: [AddApples]
# Start: on the rightmost data
# End: on the rightmost dataState: throwDecrementer
throwDecrementer, ☐ , ☐ , stop
throwDecrementer, ∀ , ∀ , evaluation, [Decrementer]State: evaluation
# Evaluates the result of the decrementer. If it is a number, add an apple. Otherwise, stop.
evaluation, 0 , 0 , → , addApple
evaluation, 1 , 1 , → , addApple
evaluation, 2 , 2 , → , addApple
evaluation, 3 , 3 , → , addApple
evaluation, 4 , 4 , → , addApple
evaluation, 5 , 5 , → , addApple
evaluation, 6 , 6 , → , addApple
evaluation, 7 , 7 , → , addApple
evaluation, 8 , 8 , → , addApple
evaluation, 9 , 9 , → , addAppleState: addApple
# Adds an apple to the next apple string, if there is room.
addApple, apple , apple , → , addApple
addApple, ☐ , apple , ← , backBackState: Backspace
# Backspaces to the initial number.
Backspace, apple , apple , ← , Backspace
backspace, ∀ , ∀ , startDecrementer
#——————————
Machine: [Decrementer]
# Decrements a natural number. If there are any 0s left, replace them with blanks. Always stops on the last digit, or the blank.
# Start: on the rightmost data item
# End: on the rightmost data itemState: Decrement
Decrement, 9 , 8 , → , transitRight
Decrement, 8 , 7 , → , transitRight
Decrement, 7 , 6 , → , transitRight
Decrement, 6 , 5 , → , transitRight
Decrement, 5 , 4 , → , transitRight
Decrement, 4 , 3 , → , transitRight
Decrement, 3 , 2 , → , transitRight
Decrement, 2 , 1 , → , transitRight
Decrement, 1 , 0 , → , transitRight
Decrement, 0 , 9 , ← , Decrement
Decrement, ∀ , ∀ , → , erase9State: transitRight
# Skips all digits up to the last digit. Stops on the last digit.
transitRight, 9 , 9 , → , transitRight
transitRight, 8 , 8 , → , transitRight
transitRight, 7 , 7 , → , transitRight
transitRight, 6 , 6 , → , transitRight
transitRight, 5 , 5 , → , transitRight
transitRight, 4 , 4 , → , transitRight
transitRight, 3 , 3 , → , transitRight
transitRight, 2 , 2 , → , transitRight
transitRight, 1 , 1 , → , transitRight
transitRight, 0 , 0 , → , transitRight
transitRight, ∀ , ∀ , ← , stopState: erase9
# Erases all consecutive 9s; stops on the last blank.
erase9, 9 , ☐ , → , erase9
erase9, ∀ , ∀ , ← , stop
Move a natural number to the left
Even though the formatting possibilities are very limited on our tape, presentation matters! Often, after a series of conversions, we need to move the result, a natural number, to a new position, usually immediately to the right of an = sign. To make things more difficult, we assume that anything can exist between the number and the = sign, including digits that are not part of the number to be transferred. When moving, all signs present between the number and the = sign must be erased (i.e., replaced by a blank). The machine must stop on the = sign. Here, the symbol ∀ will be of great help. Initially, the head must be positioned on the first digit forming the number to be moved (i.e., the left-hand digit). Finally, it must be positioned on the “=” sign.
Example: starting situation: =☐ 1 2 3 xyzt 5 8 4☐ ☐ ☐ ( head positioned on 5: move 584)
Arrival status: =584☐ ☐ ☐ ☐ ☐ ☐ ☐ ☐ ☐ ☐ ☐
Obviously, the machine shouldn’t crash if the number is already correctly positioned after the = sign. And if you use my X and Y technique described below, it shouldn’t crash if there’s only one box between the = and the first digit.
The collection is C={the entire collection of signs defined on Actilud}.
Here, we will have to memorize the numbers that we move. With the Turing machine, the only possibility of memorizing information is to use a state for each piece of information to be memorized . Among the states necessary for operation, we will have to create as many as there are signs to be transported, i.e. 10.
Here, we have to memorize the digits we move. With the Turing machine, the only way to memorize information is to use a state for each piece of information to be memorized. We’ll need to create as many states as there are signs to be transported, i.e. 10, in addition to the other states.
Of course, there are several ways to implement the program. Programming certain states is quite repetitive; so, to save the number of states to program, my idea was the following. First, we clean the strip between the = sign and the first number. We delimit the space between the = and the first number with two letters, X and Y. The segment [X,Y] moves as we move a number after those already placed to the right of =. The letter Y allows us to test the end of the program: if there are no more numbers to the right of Y, it’s over. X marks the location of the box in which we must place a number. If we don’t use this trick, we have to create 10 additional states just to place a number to the right of the = sign! (note that instead of using X and Y, we could have used only X).
Of course, there are several ways of implementing the program. Programming certain states is rather repetitive; so, to save the number of states to be programmed, my idea was as follows. First, we clean up the strip between the = sign and the first digit. The space between the = and the first digit is delimited by two letters, X and Y. The segment [X,Y] moves as you move a digit following those already placed to the right of =. The letter Y is used to test the end of the program: if there are no more digits to the right of Y, it’s over. X marks the location of the box in which to place a digit. If you don’t use this trick, you’ll need to create 10 additional states just to place a digit to the right of the = sign! (note that instead of using X and Y, we could have used X only).
Here is the listing (spoiler)
Machine: [MoveNumberToEqualLeft]
# Start: on the leftmost digit of the number to be transferred
# End: on the = signState: initialize
# Leave the pointed digit to prepare the tape
initialize, ∀ , ∀ , ← , fill blanksState: fill in blanks
# Fill the boxes to the left with blanks up to the sign =
fill in blanks, ‘=’ , ‘=’ , → , set X
fill in blanks, ∀ , ☐ , ← , fill in blanksState: set X
# After finding the = or dropping a number, drop an x and go looking for the Y or a number.
set X, ☐ , X , → , search Y
set X, Y , X , → , pickNumber
set X, ∀ , ∀ , ← , return to equalState: takeNumber
# If a number is found, enters the corresponding move state. Otherwise, return to equal and stop.
takeNumber, 0 , Y , ← , move0
takeNumber, 1 , Y , ← , move1
takeNumber, 2 , Y , ← , move2
takeNumber, 3 , Y , ← , move3
takeNumber, 4 , Y , ← , move4
takeNumber, 5 , Y , ← , move5
takeNumber, 6 , Y , ← , move6
takeNumber, 7 , Y , ← , move7
takeNumber, 8 , Y , ← , move8
takeNumber, 9 , Y , ← , move9
takeNumber, ∀ , ∀ , ← , return on equalState: search Y
# Searches for the Y previously placed on the strip. If a number is found in place of the Y, go to the Take Number state without moving. If the Y is found, delete it, go right and go to the Take Number state.
search Y, ☐ , ☐ , → , search Y
search Y, Y , ☐ , → , takeNumber
search Y, 0 , 0 , takeNumber
search Y, 1 , 1 , takeNumber
search Y, 2 , 2 , takeNumber
search Y, 3 , 3 ,
takeNumber search Y, 4 , 4 , takeNumber
search Y, 5 , 5 ,
takeNumber search Y, 6 , 6 ,
takeNumber search Y, 7 , 7 , takeNumber
search Y, 8 , 8 , takeNumber
search Y, 9 , 9 , takeNumberState: return on equal
return on equal, ☐ , ☐ , ← , return on equal
return on equal, X , ☐ , ← , return on equal
return on equal, ‘=’ , ‘=’ , stop
return on equal, 0 , 0 , ← , return on equal
return on equal, 1 , 1 , ← , return on equal
return on equal, 2 , 2 , ← , return on equal
return on equal, 3 , 3 , ← , return on equal
return on equal, 4 , 4 , ← , return on equal
return on equal, 5 , 5 , ← , return on equal
return on equal, 6 , 6 , ← , return on equal
return on equal, 7 , 7 , ← , return on equal
return on equal, 8 , 8 , ← , return on equal
return on equal, 9 , 9 , ← , return on equalState: move0
move0, ☐ , ☐ , ← , move0
move0, X , 0 , → , drop XState: move1
move1, ☐ , ☐ , ← , move1
move1, X , 1 , → , drop XState: move2
move2, ☐ , ☐ , ← , move2
move2, X , 2 , → , drop XState: move3
move3, ☐ , ☐ , ← , move3
move3, X , 3 , → , drop XState: move4
move4, ☐ , ☐ , ← , move4
move4, X , 4 , → , drop XState: move5
move5, ☐ , ☐ , ← , move5
move5, X , 5 , → , drop XState: move6
move6, ☐ , ☐ , ← , move6
move6, X , 6 , → , drop XState: move7
move7, ☐ , ☐ , ← , move7
move7, X , 7 , → , drop XState: move8
move8, ☐ , ☐ , ← , move8
move8, X , 8 , → , drop XState: move9
move9, ☐ , ☐ , ← , move9
move9, X , 9 , → , drop X
