Requiring little material: two pawns, two L-shaped tokens of different colors, a 4×4 checkerboard, and having very simple rules, the L game is educationally very interesting because it allows the development of the spatial representation of objects. It is a fun application of the concepts of translation, symmetry and rotation.

The rules of the L game

Two players take turns opposing each other. One player holds the red L, the other the blue L. The other two pieces are neutral, meaning they belong to both players. Initially, the grid is in the following situation:

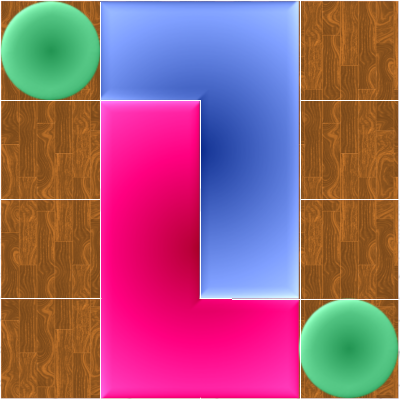A random draw can be made to determine who goes first. The player with the lead must first move his L to an empty spot on the grid. To do this, he can use any combination of the following transformations:

• translation: a linear movement from one location to another
• rotation of 90°, 180° or 270°
• symmetry: left/right inversion, top/bottom, or both.

On Actilud, the player uses the buttons on the toolbar to perform transformations.

The player has lost if it is impossible to move his L to a new position.

Once his L is placed in a new position, the player can, if he wishes, move one of the two pawns to the empty square of his choice.

On Actilud, the player can move one of the two green pawns to a new empty square, or click on one of the two pawns without moving it to indicate the end of his turn.

The aim of the game is to position the pieces in such a way as to block your opponent.

The strategy

There are exactly 15 winning positions, regardless of rotations and symmetries. This Wikipedia article will give you all the details . Here are those 15 positions, reproduced from the Wikipedia article.

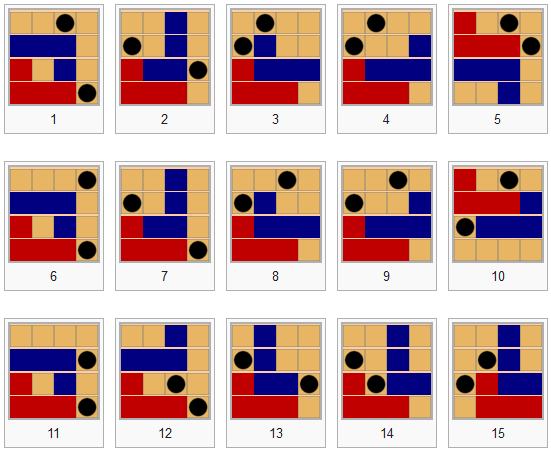
If you look closely at the blue L, you’ll see that at no point does it touch any of the corners. The winning strategy is therefore to avoid placing your L on the corners. If you manage to reproduce one of these 15 figures (or their symmetry/rotation), you’ve won. Just as there are winning positions, there are also losing positions to avoid! I refer you to the Wikipedia article. Of course, all losing positions use one of the corners of the grid.

So there’s a strategy that, while not guaranteed to win, does prevent you from losing. Two “perfect” players are guaranteed to play forever!

Player versus player

It’s undoubtedly the most fun way to approach this game, because it involves the human dimension! A little camaraderie and competitive spirit always improves results. What’s more, if you’re running a class, it’s often easier to put two students in front of a machine. This is the approach I recommend for introducing this game.

As I point out at the end of the article, the game can also be made and used in the classroom without any computer support. Then, once the students have mastered the rules, they can be introduced to the winning strategy of avoiding corners, and play individually against the computer to improve their performance.

Player versus machine: the algorithm used on Actilud

The algorithm on Actilud is is fully capable of never losing. I’ve carefully programmed all the winning and losing situations into it, and it works! But who wants to fight a machine that can’t lose? So there are 5 difficulty levels, all of which can lose.

The good loser level

The good loser level is probably best suited to beginners and those who are reluctant to make an effort (although…). In this level, it will be very difficult for the player to lose, because the algorithm carefully avoids playing the 15 winning situations… and plays randomly among the remaining combinations. But be careful, the computer can still win if the player is placed in one of the 14 losing positions!

As a result, games can last a long time, especially if the player plays as badly as the computer.

The goal here is to get students to anticipate their opponent’s moves, giving them a good chance of winning if they apply themselves. If they try not to use corners at this level, they should win sooner or later!

The good comrade level

In this level, the computer always plays badly; as in the previous level, it randomly draws a combination from the list of possible moves while eliminating winning situations 3 times out of 4. This therefore ultimately gives a low probability of winning, but the computer is still very distracted.

The objective is the same as in the previous level.

The expert level

This is actually an average player level. This time, the computer prioritizes strategy by trying to avoid corners. Move choices are made as in the Good Friend level, so the computer, still distracted, may still miss a possible winning move.

The master level

Here, the computer is not distracted at all. If it happens to be able to place one of the 15 winning combinations, it makes no bones about it! Otherwise, he avoids playing in corners, preferring moves that force his opponent to play in a corner. A difficult but interesting level. The computer is a good player here.

The Grandmaster level

This level works like the master level, but the computer predicts a move in advance and puts the opponent in the position of not being able to make a winning move on his turn. However, it doesn’t go any further. To win, the player has to get the computer into one of the 14 losing situations, by forcing it into a corner. Good luck with that! Personally, I’ve never managed it.

At the very beginning, I added the “invincible infernal machine” level, in which the program also avoided losing situations. In other words, the games could last a long time but were not really satisfying, because the machine had become a “perfect” player! The only satisfaction you could derive from the game, at this level, was to last as long as possible against it!

Interest and limits of the site

Particular care has been taken in the representation of rotation and symmetry; a short animation shows the pieces rotating or reversing. Translation is manifested by the displacement of the computer’s L. This is important for mental representation. However, be careful, this remains a screen representation, therefore in two dimensions.

This game can easily be made by the pupils themselves with a bit of strong cardboard; it’s an opportunity to do some practical geometry: use the ruler, compass and square, draw lines and right angles. At the end of the project, we don’t just hand the work back to the teacher and wait for a grade. We play with it. Which brings the satisfaction of reusing self-created material.

Manipulating the cardboard L helps to assimilate symmetry and rotation; indeed, manipulating real objects is a necessary step in the construction of a coherent representation of the world; the virtual can accompany and enable us to go further, it can even replace concrete manipulation, but only when the brain has already had sufficient real-life experience in the field.

Start the activity.