The game “Mass and Weight Across the Solar System” helps you understand the difference between mass and weight. It’s also a good way to practice the concept of framing. Through the game’s genesis, this article details the principles involved and their consequences. Finally, we’ll understand why it’s difficult to weigh a lemon on Phobos.
The principles
Mass is a value that measures the quantity and quality of matter. Mass is measured in grams (g). For example, one liter of molten lead is heavier than one liter of molten glass.
Mass exerts an effect on space-time: gravity. The greater the mass, the stronger the gravity. In space, each celestial body exerts its own attraction on its surroundings and is subject to that of others, depending on its mass and the distance separating it from other masses.
On Earth, we have instruments that allow us to precisely measure gravity. The higher you go in a balloon, the more gravity decreases, because you move away from the center of gravity. But if you position yourself above a large rocky massif, like a mountain, it increases, because the mass beneath the balloon is greater.
Weight is a value that measures the action of gravity on mass.
Mass and weight are related by the formula: P = Mg, where P is weight expressed in Newtons (N), mass is expressed in grams and g is the coefficient of gravitation, expressed in m/s² (meters per second squared).
Consumer devices that measure weight are rarely graduated in newtons. Instead, kg or g are used. In this case, the previous formula remains valid, but the units change. Weight is expressed in “grams,” which, for a physicist, is rather an error. Therefore, to differentiate, we will speak of “gram-force” or “gram-weight.” The coefficient g no longer has a unit and is equal to 1, and therefore we have P=M.
Bathroom scales and electronic table scales, which are used in the kitchen to measure flour or sugar, are the most common weight-measuring devices. These devices operate using a spring that compresses to varying degrees depending on the weight placed on the scale. These scales are sensitive to changes in gravity.
To measure mass, we use a Roberval balance. However, to work, a Roberval balance also needs gravity! Try operating it in a weightless space station! You’ll have some trouble moving the scales.
So why do we say that the Roberval scale measures mass?
Since the plates are close together, we consider that the gravity acting on the left plate is the same as that acting on the right plate.
On Earth, an orange weighs about 200g. I place my orange on the left pan and add the equivalent of 200g in marked masses to the right pan. I obtain a balance.
If I now go to the surface of the sun, the orange no longer weighs 200g but 5.6kg-weight! But the marked masses will also be heavier, in the same proportion. I place the orange on the left-hand pan: it descends. To restore balance, I place 200g of marked masses on the right-hand pan. This amounts to placing 5.6kg-weight. We ultimately obtain the same balance as on Earth. The measurement on the Roberval balance therefore does not depend on gravity.
This is in theory. But in practice, things are a little more complicated.
The genesis of the game
When I initially programmed the Roberval scale, and later the electrical scale, I included the formula P=Mg with the parameter g , which indicates the ratio between gravity coefficients. This ratio is equal to 1 for Earth’s gravity. The idea was to be able to easily create a game where I could simply modify this parameter to simulate another star. Since gravity is 28 times higher on the Sun, I simply replace the value 1 with 28, and that’s it.
But when I finally created this game, things weren’t as simple as I initially thought…
The mass of fruits and vegetables and the precision
First of all, you should know that fruits and vegetables have a mass that is randomly generated to mimic nature as closely as possible. A lemon, whose measured mass is 113g, can have a different effective mass. Here, it is 112.84453671587923g.

Objectively, the left-hand, heavier pan should be tilting downward. Why is this balanced? Look at the illustration above. At the bottom of the scale is the word “0.5g.” This indicates the accuracy, which is ±0.5g. The difference between the lemon’s mass and the marked masses is within the accuracy limits: -0.5g < (112.84453671587923 – 113)g < 0.5g, and this is why the pans balance.
Accuracy is a measure of frictional forces. Our scale attempts to adhere to the laws of nature as closely as possible, and so frictional forces are also simulated. Here, they have been adjusted to allow the use of the smallest possible marked mass, 1g. Our scale is only accurate to the nearest gram.
In the virtual weighing game, the accuracy has been reduced to ±5g (the smaller the accuracy, the larger its value!):

The lightest object is the blue triangle, which has a mass of 10g. To balance the boards, we must therefore reduce the precision; it is to the nearest decagram. Moreover, in this game, we cannot find a cherry, because the mass of a cherry may be too low to counterbalance the frictional forces. If we place a cherry on an empty board… well, nothing happens.
Meet on Phobos
Phobos, one of Mars’s two natural moons, is so light that it looks more like a pebble. The force it exerts on nearby bodies is too weak for it to clump together and resemble the other planets.

Gravity on Phobos is much weaker than on Earth. And this is where the trouble begins if you want to weigh a lemon on Phobos:

Lemon is much too light! You need a much heavier fruit. Melon, for example:
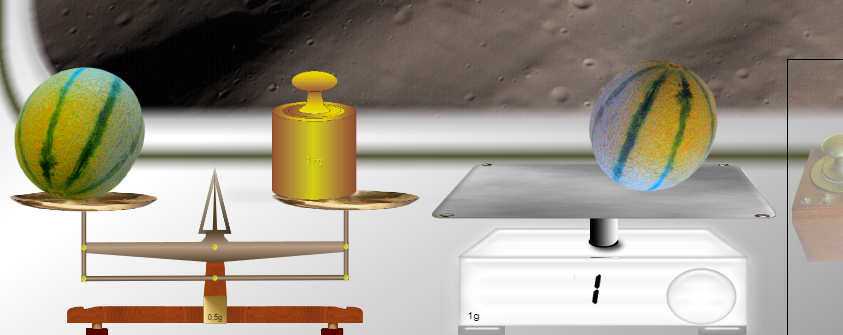
The spring scale barely moves and measures a weight of 1g. The Roberval scale, on the other hand, balances for all masses between 430g and 2429g:

Why this phenomenon? Because of the precision of the scale, of course! Be careful, the friction forces are the same, whether on Phobos or on Earth. The precision interval, expressed in grams, does not change; but its value expressed in g-weight is modified, because of the lighter gravity. A mass marked 200g weighs only 0.1g-weight on Phobos. This is insufficient to activate the scales. See below the calculation of the limit weight interval. For Phobos, the interval is ]-1000g-weight, +1000g-weight[ (the limits are open, that is to say that the scales will move from a difference of ±1000g-weight). As long as the difference in weight between the two pans is between these two limits, the scale will not move. The scales move as soon as one of the two limits is reached or exceeded. The interval therefore has a range of 2000g-weight, from which we subtract 1 because of the open limits, i.e. 1999g-weight. We measured this range with the two weighings above: it represents the absolute value of the difference between the two weighings that we carried out: | 2429 – 430 | = 1999.
Note: The melon’s mass can be correctly estimated by averaging the two measurements. But we don’t go that far in the game. Here it is 1429.5 g to within ±0.5 g.
Ultimately, for Phobos, our scale is not accurate enough. I’d better replace it with a much more accurate model.
To make this game, I could have modified the precision of the scales, which, on Earth (but not on Phobos, of course) would have required weighing with the decigram, the centigram and the milligram. However, it is already complicated enough to weigh correctly down to the gram. There is also an ergonomic problem, that of the size of the masses marked increasingly lighter, and therefore visually smaller, which must nevertheless remain large enough to be grasped with the mouse or the finger. I therefore abandoned the idea.
I could also have adjusted the scale’s accuracy based on gravity. But this would have misled players – the idea is to use the same device on all the planets and stars and definitely not change it in between.
This is why what I intended to be a simple weighing game ultimately became a game of framing a weighing interval. On low-gravity planets at least.
See you on the Sun
Our spacecraft has a magnetic field strong enough to push particles away! Otherwise, it wouldn’t have been able to pass through the solar corona, which has a hellish temperature of a million degrees, and then withstand the surface temperature of 5,500°.
Here, gravity is much higher. Let’s see what happens and take our lemon again. On the spring scale, it weighs about 3200 g.

Let’s move on to the Roberval scale. There, we encounter another surprise: it’s impossible to balance the scales!


What’s going on? Again, it’s a matter of precision.
The masses placed on the trays are 28 times heavier than on Earth. So, a mass marked 1 g will weigh 28 g on the Sun.
Now, our lemon, which does not weigh a precise number of grams, cannot be weighed correctly. It is either too heavy or too light. All we can do is frame it in: 124g < mass of lemon <125g
On the sun, our Roberval scale has become far too precise. To get a better measurement, you need to use lighter marked masses, or reduce the scale’s precision!
And the melon?
Fortunately, our scales are of very good quality. The Roberval scale is a simulation of very solid steel. As for the spring scale, it is capable of absorbing very heavy objects, even if the maximum tolerated threshold is exceeded, and this without wear. However, the melon has no chance of being weighed on it:

Calculate the weight limit interval
This interval is the one in which a difference in weight between the trays has no effect. Calculating the limit weight interval is quite simple. We take the lower and upper values of the precision interval and divide them by the gravity coefficient.
The default precision interval is -0.5g, +0.5g
Here are the different gravity coefficients used in the game:
Sun: 28.02
Mercury: 0.377
Venus: 0.905
Earth: 1
Moon: 0.1657
Mars: 0.379
Phobos: 0.0005
Jupiter: 2.528
Europa: 0.133
Saturn: 1.065
Uranus: 0.886
Neptune: 1.137
On Earth: ]-0.5g-weight, +0.5g-weight[ The scale tips as soon as the difference between the two pans is 0.5g-weight.
On Phobos:] -1000g-weight, +1000g-weight[ The scale tips if the difference between the two pans is at least 1000g-weight. Below that, it will not move.
On the Sun: ]-17.8mg-weight, +17.8mg-weight[ If we weigh a fruit or a vegetable, the pan most of the time tips to one side or the other, because the difference between the pans is most often outside the indicated range, given that we use marked masses limited to the gram.
 Link to Activity: Mass and Weight Across the Solar System
Link to Activity: Mass and Weight Across the Solar System
