Merging is the inverse of repercussion. The technique can find pivot cells that are false, and, in some cases with Booleans, true cells . Two rows can produce a false pivot cell if combining the two rows results in a false row.

NB: You must have a good understanding of the repercussion technique before tackling this.

By rotation…

Let’s look at the example below:

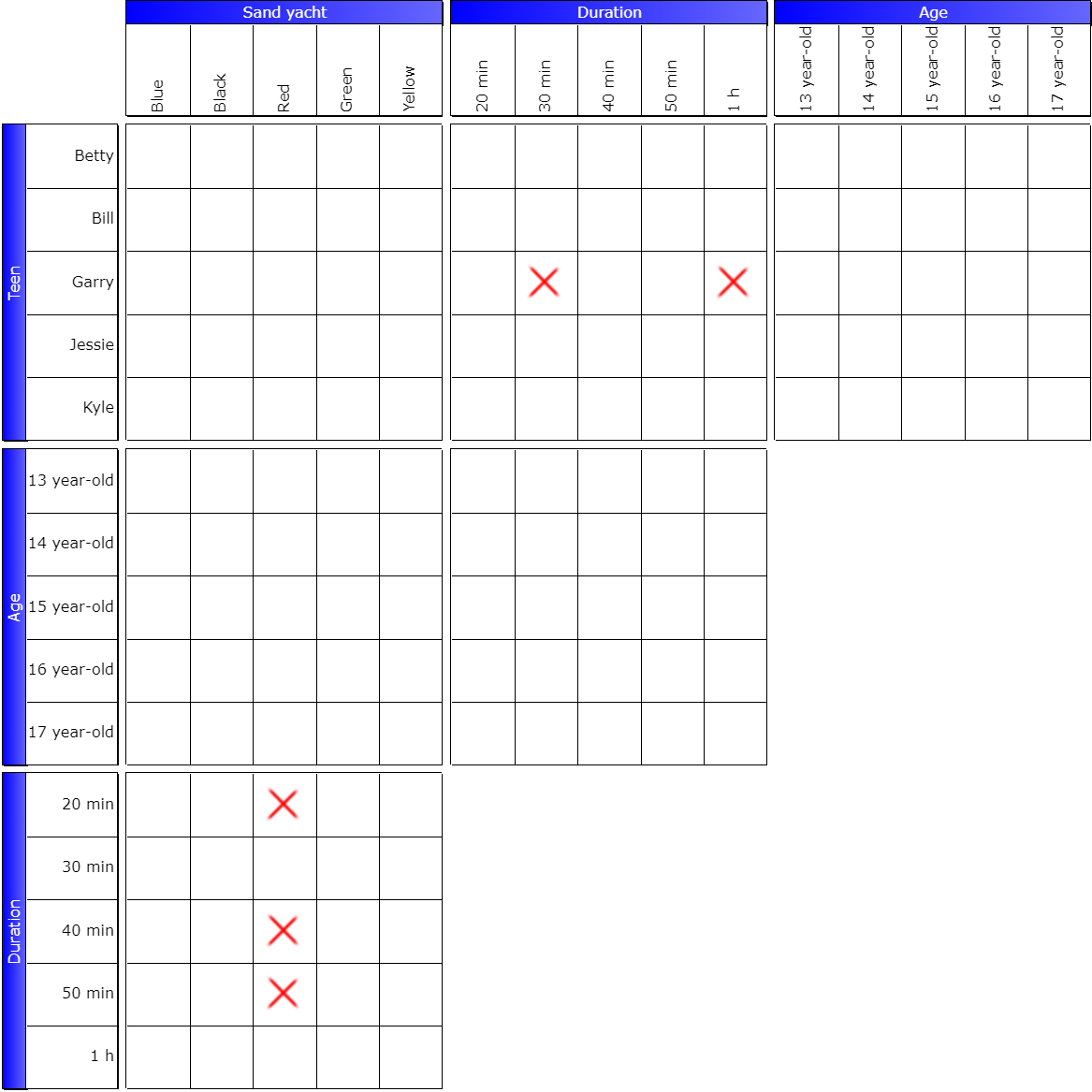
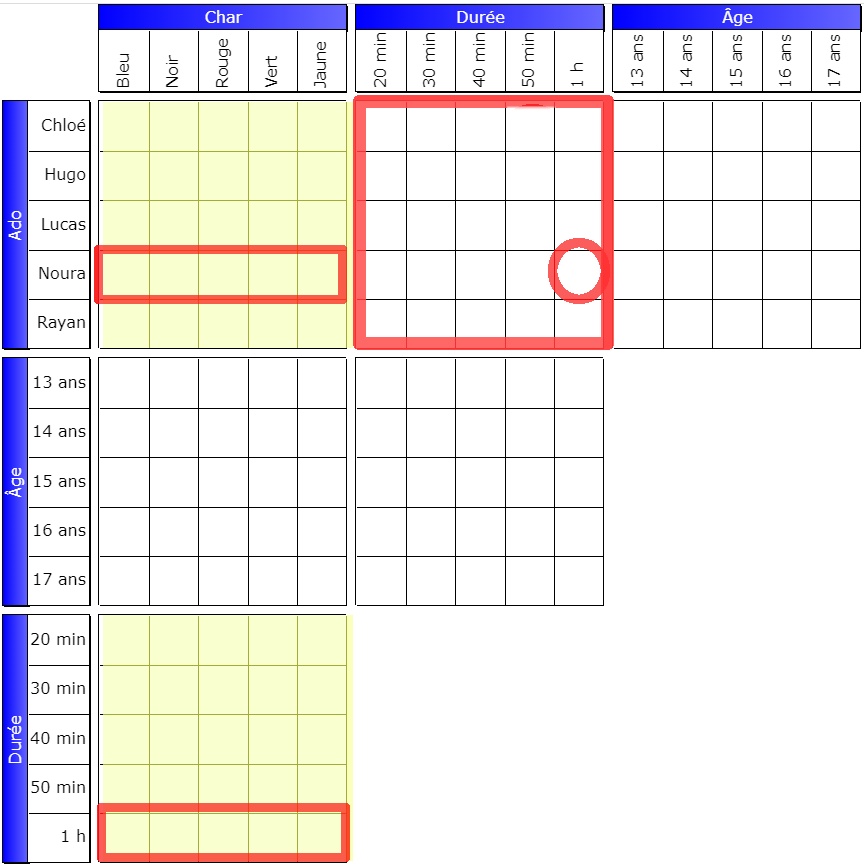
Garry doesn’t drive for 30 minutes and an hour; as for the red yacht driver, he doesn’t drive for 20, 40, and 50 minutes. So the question is: Does Garry drive a red yacht?

The answer is no, of course, because if it were, he couldn’t drive for any of the times shown! Which isn’t possible, of course, since by definition, you need one true sign per row.

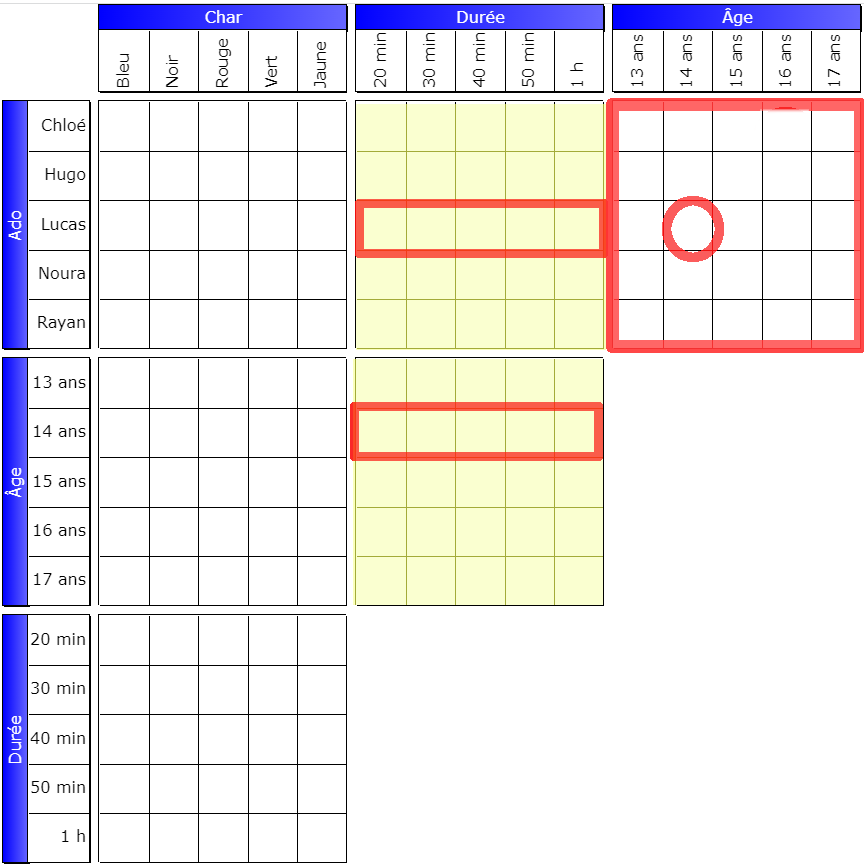
There’s a more visual way to figure this out. Let’s first find the pivot box:

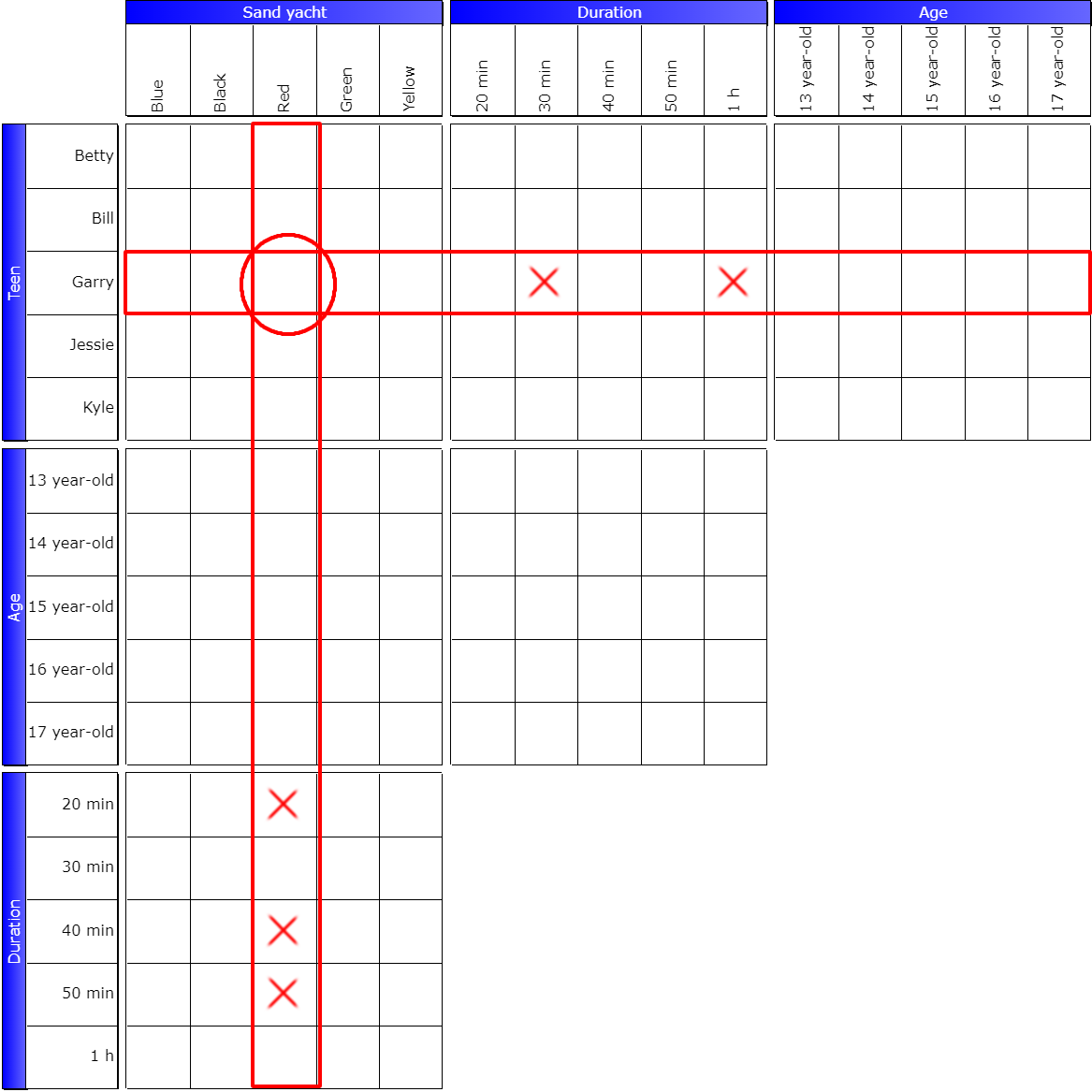
It is (Garry, Red). But this time, when we perform a repercussion between the two grids, we obtain an impossible result:

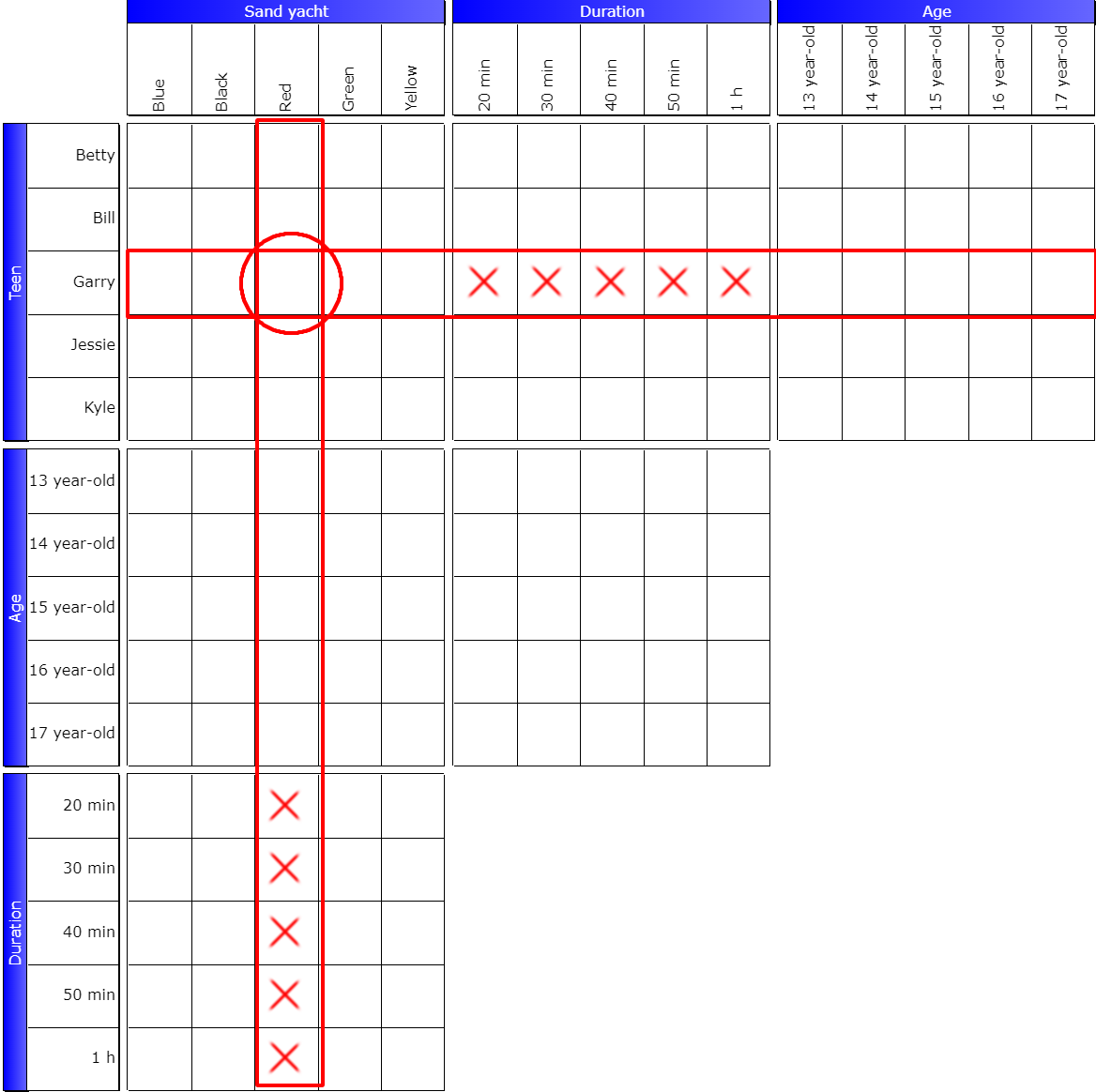
Since this event cannot occur, the pivot box is therefore necessarily false:

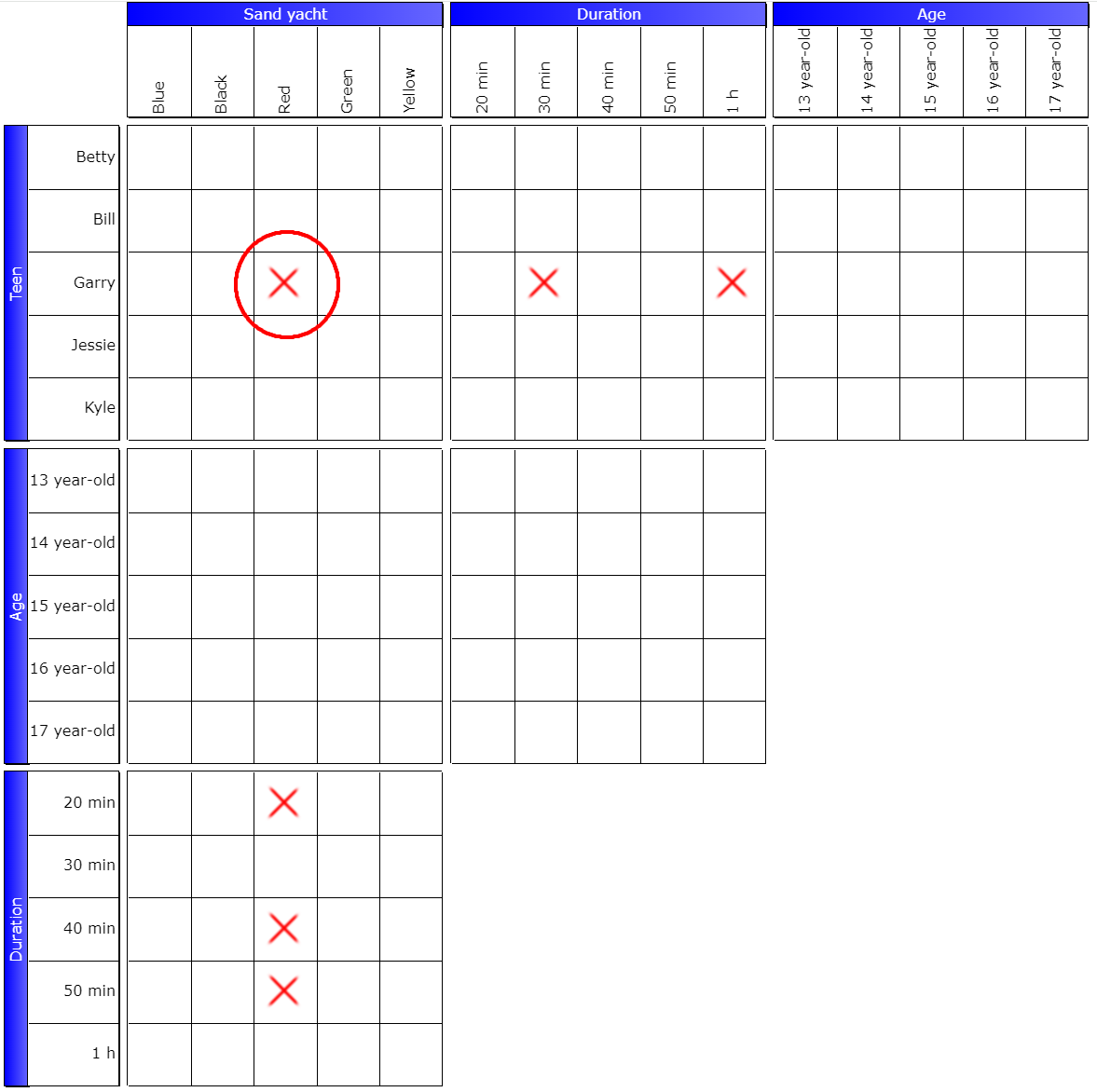
By translation

What is true by rotation is also true, of course, by translation.

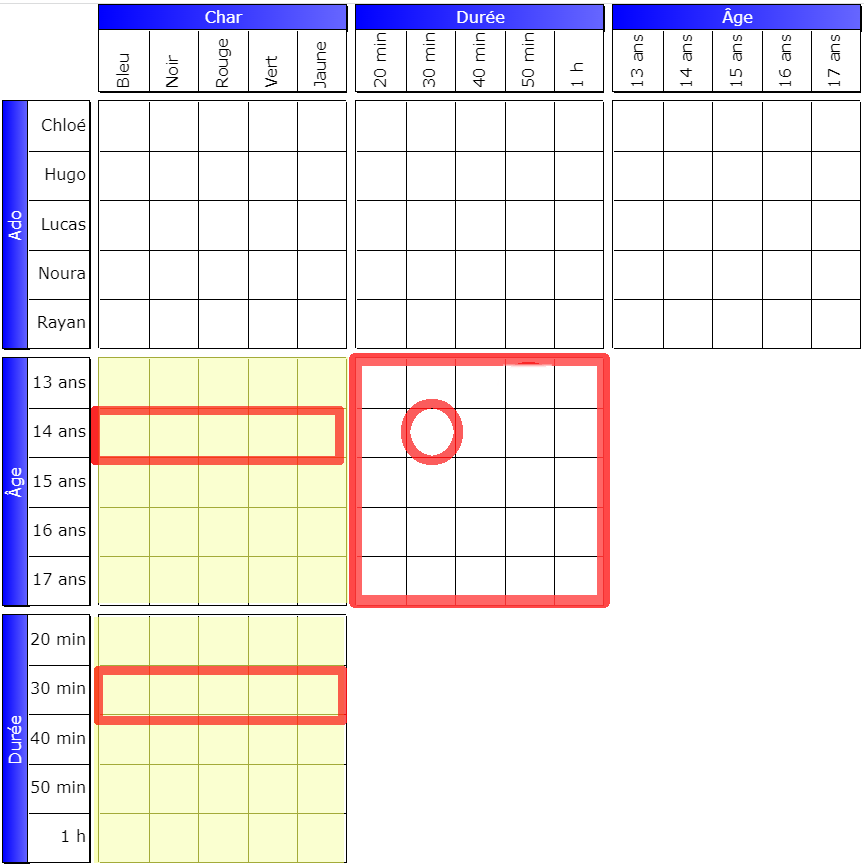
The 14-year-old doesn’t drive for 30 minutes. If we translate the two columns, we realize that we get a column of false signs.

Merging technique and Booleans

Find false boxes

Merging is even more interesting when it occurs with Booleans; if it shows a contradiction, then surely the pivot box is false.

Let’s look at the -very simplified- example below:

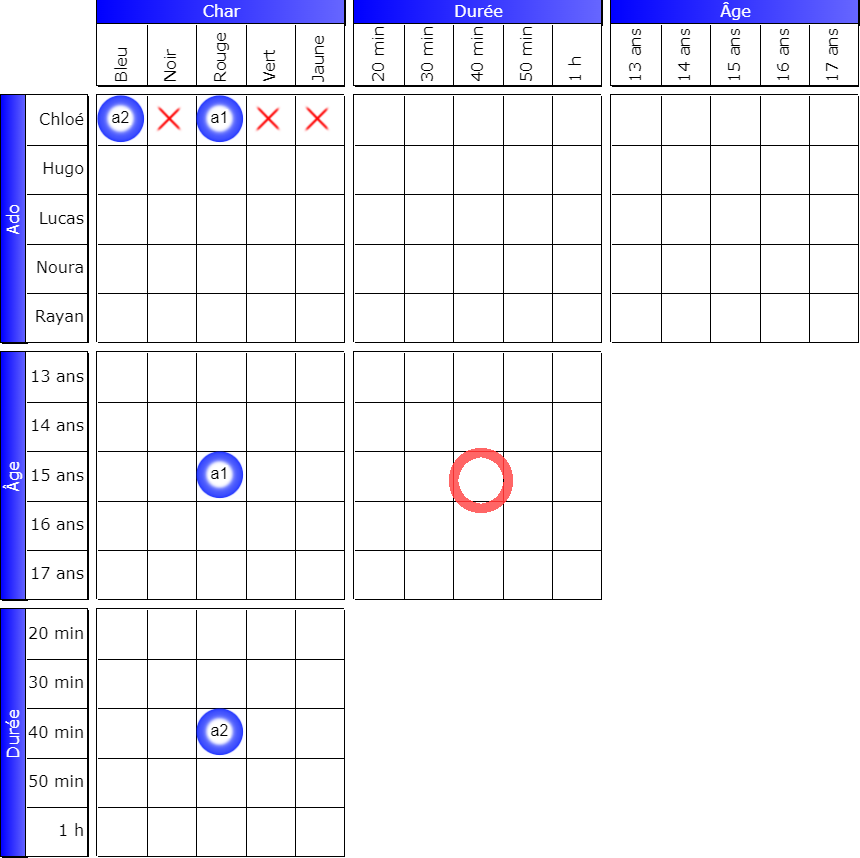
First, notice that Chloe is driving either a blue yacht or a red yacht. Therefore, one of the two Booleans, a1 or a2, must be true, but they cannot both be true: a1 ≠ a2

Let’s ask ourselves the following question: can a 15-year-old drive for 40 minutes?

If the answer is true, then we have created a true pivot between the 15 years and 40 min lines :

So, we need to mirror the two lines , which produces the superposition of a1 and a2. This means that a1 = a2! But this contradicts what we already know. So the 15-year-old can’t drive for 40 minutes.

And Chloe? Can she drive for 40 minutes? No, for the same reason.

You see that the merging technique gives particularly interesting results with Booleans.

Find true boxes

Sometimes, the merging technique still allows us to discover true signs:

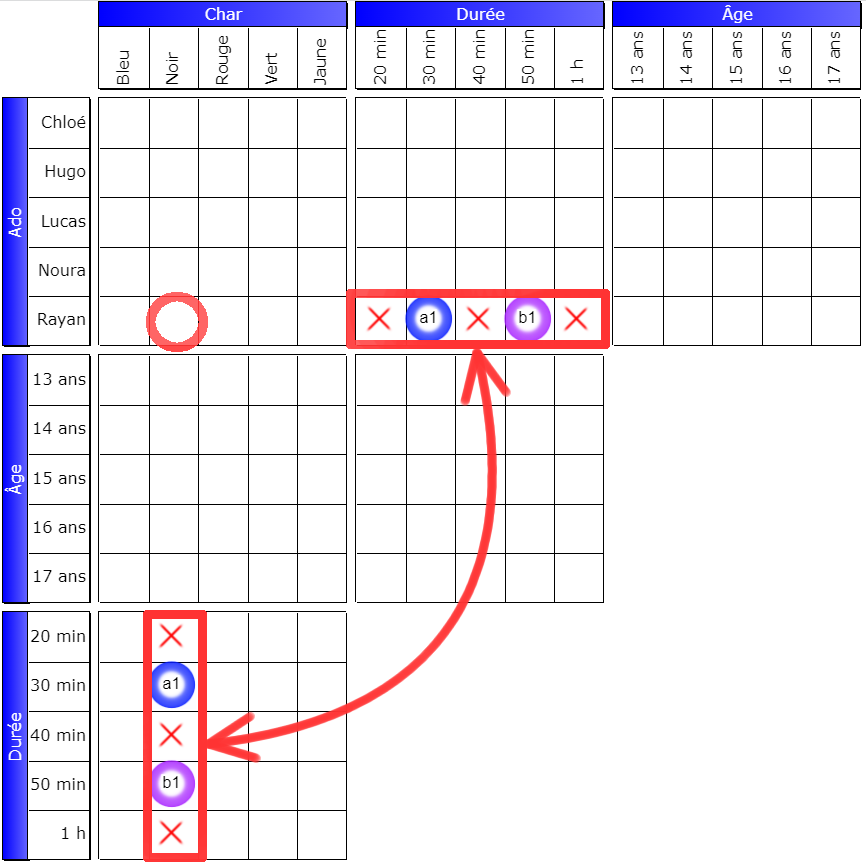
Does Rayan have a black yacht? The answer is yes! Because if we superimpose the two rows corresponding to the pivot, we see that they are strictly identical. So, regardless of the state of Booleans a1 and b1, we can safely say that yes, Rayan is indeed driving the black yacht!

Note: this only works if each row has no empty boxes.

Find the pivot boxes

For the sake of simplicity, we will call “pivot” not only the boxes around which rotations are performed, but also those from which translations are performed – even if, strictly speaking, it is no longer really a “pivot”.

By rotation

The pivot boxes by rotation are located on the central grids:

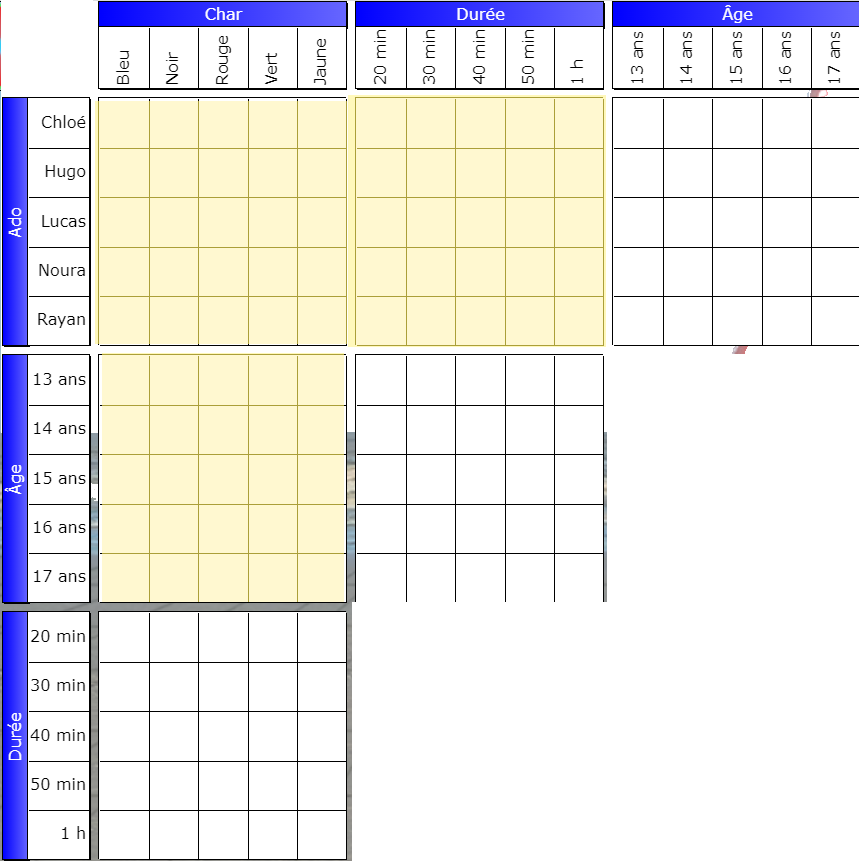
Here is where the peripheral grids are located when the central grid is first (Teen, Yacht):

Here is the rotation for the second grid (Teen, Duration):

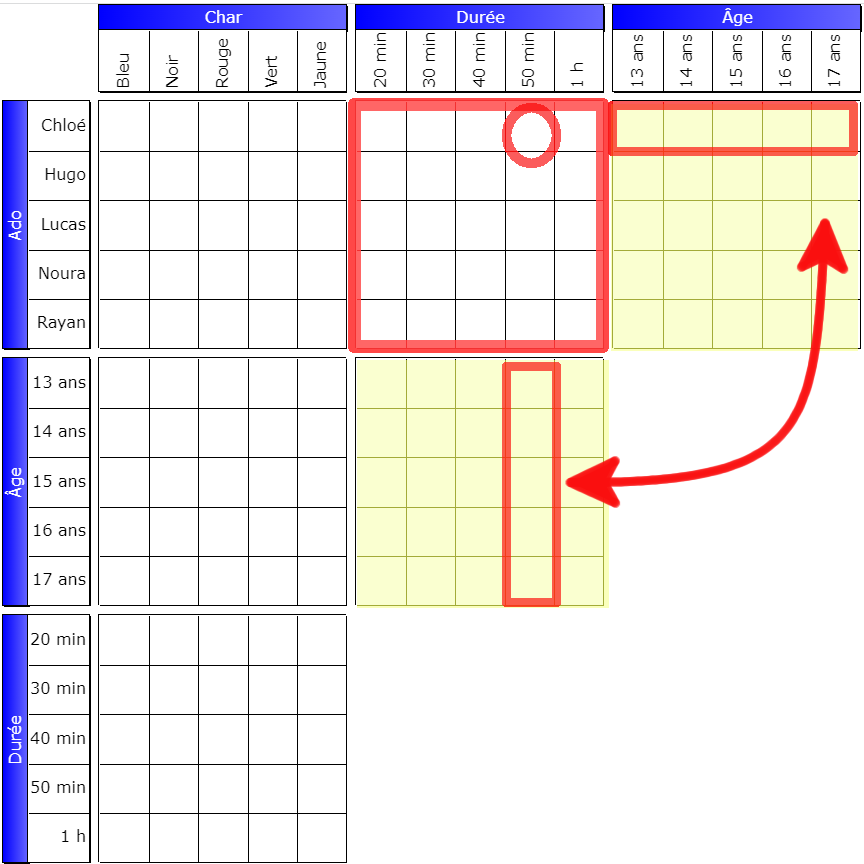
Here is the third central grid, (Age, Yacht)

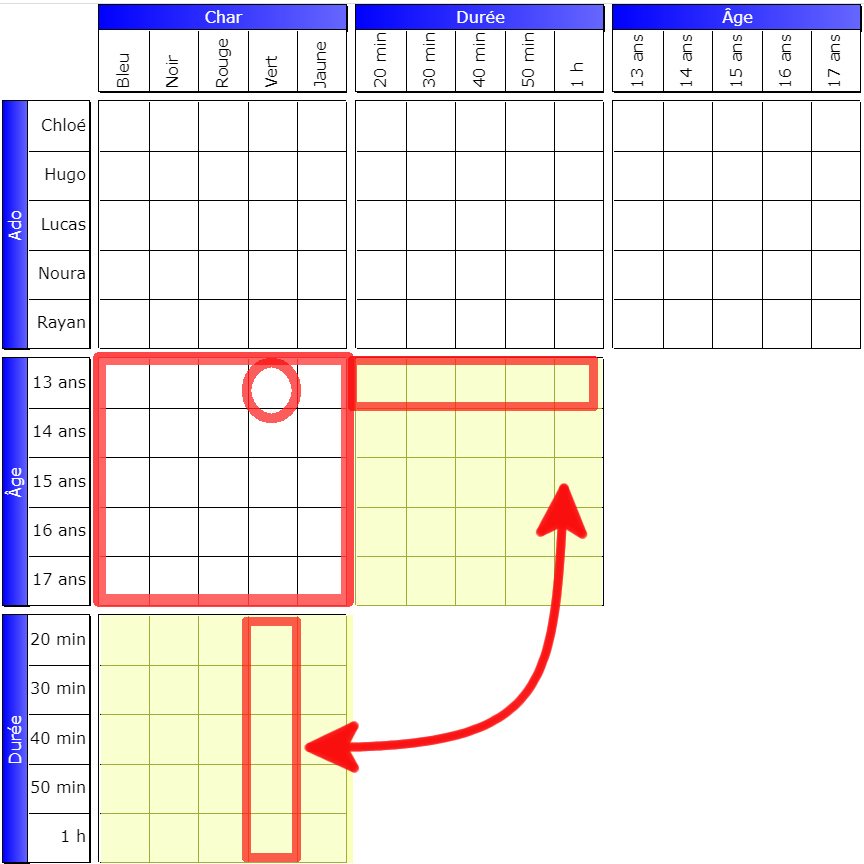
By translation, columns

The grid containing the pivot is always located below the left grid. The pivot box is at the intersection of the two column headers: (15 years, 30 minutes) for the first example.

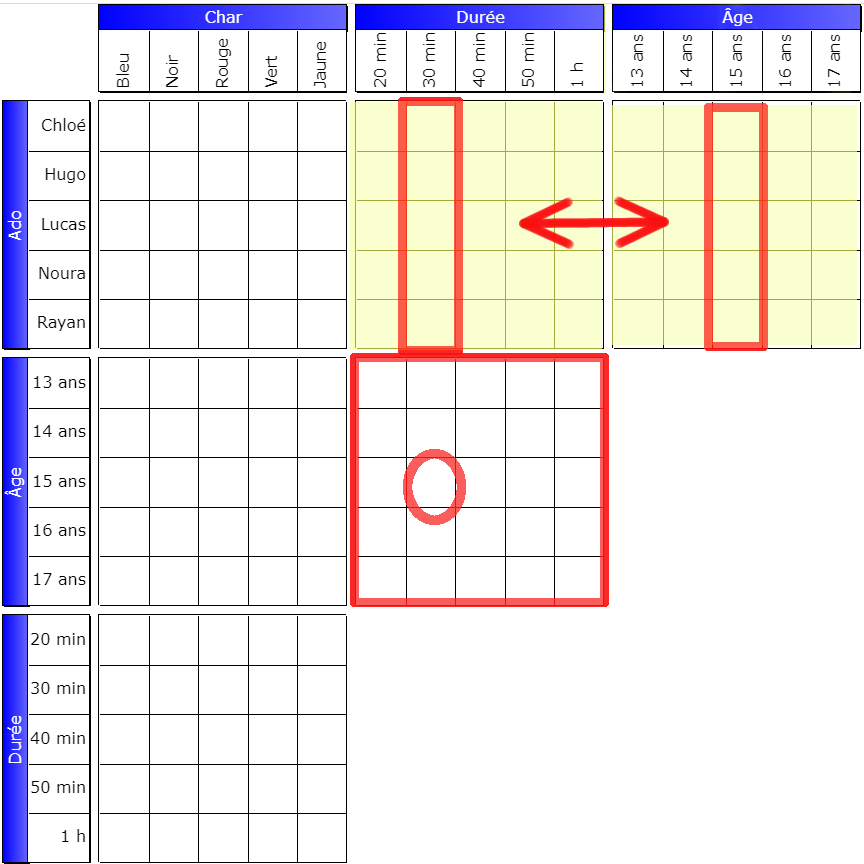
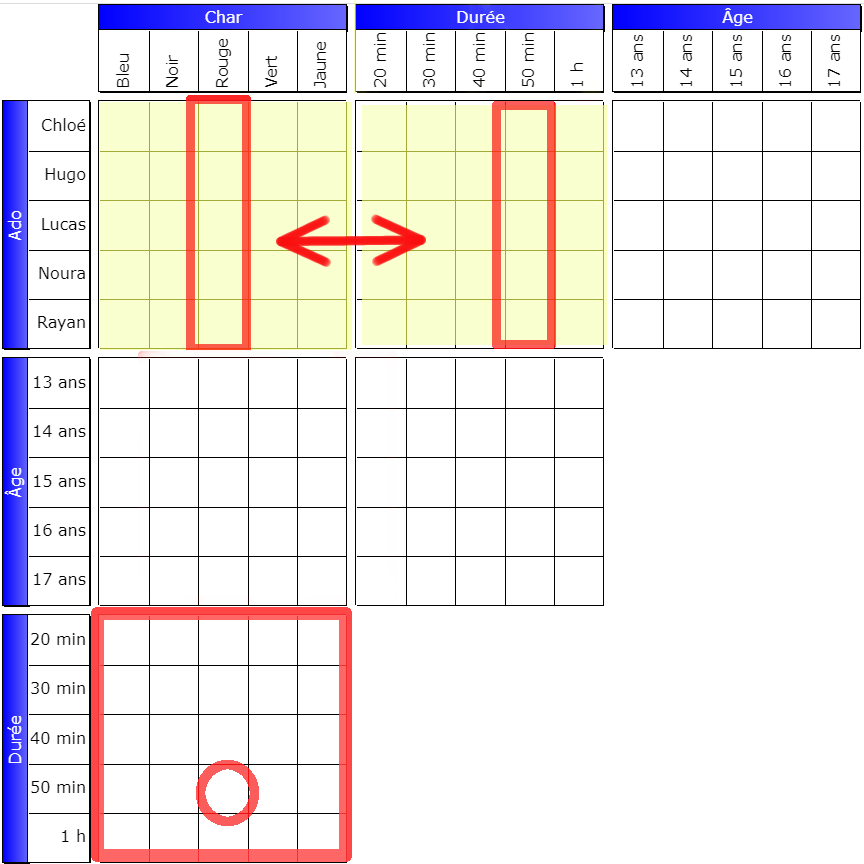
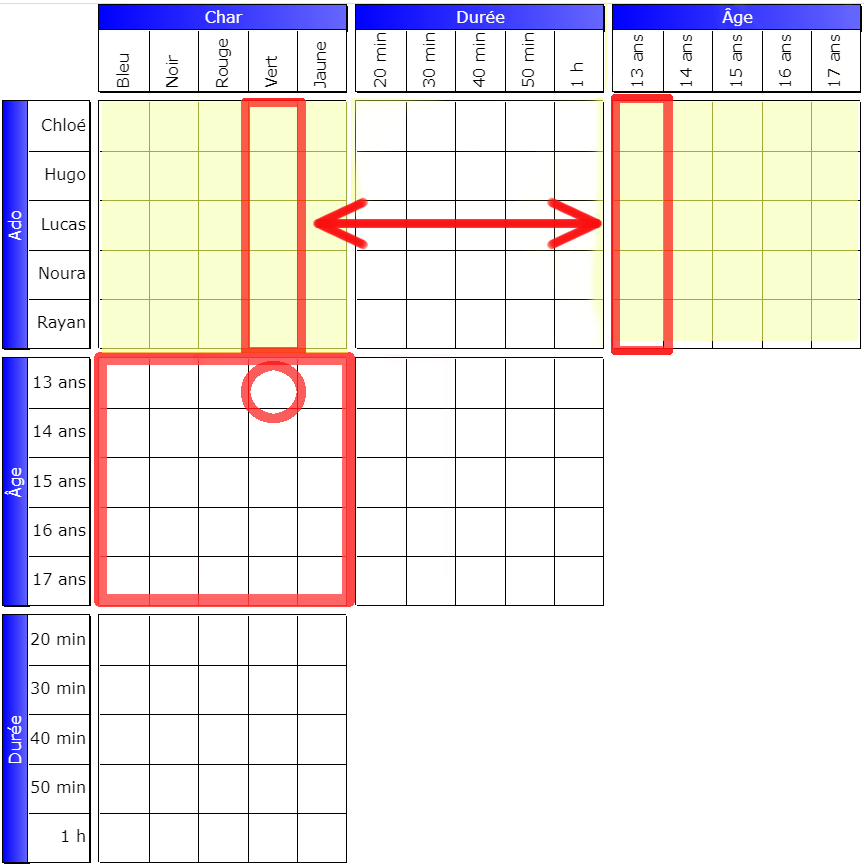
By translation, lines

The pivot grid is always to the right of the top grid. The pivot box is at the intersection of the headers of the rows concerned; it is the box (Garry, 14 years old) in the first example.