Let an alternative be formed of n Booleans. Any cell located at the intersection of the n Booleans of the alternative is false.
The technique is simple when applied to a single grid, which is what motivated the creation of this rule.
When applied to different grids, the technique is a reprise of the merging technique with Booleans forming an alternative.
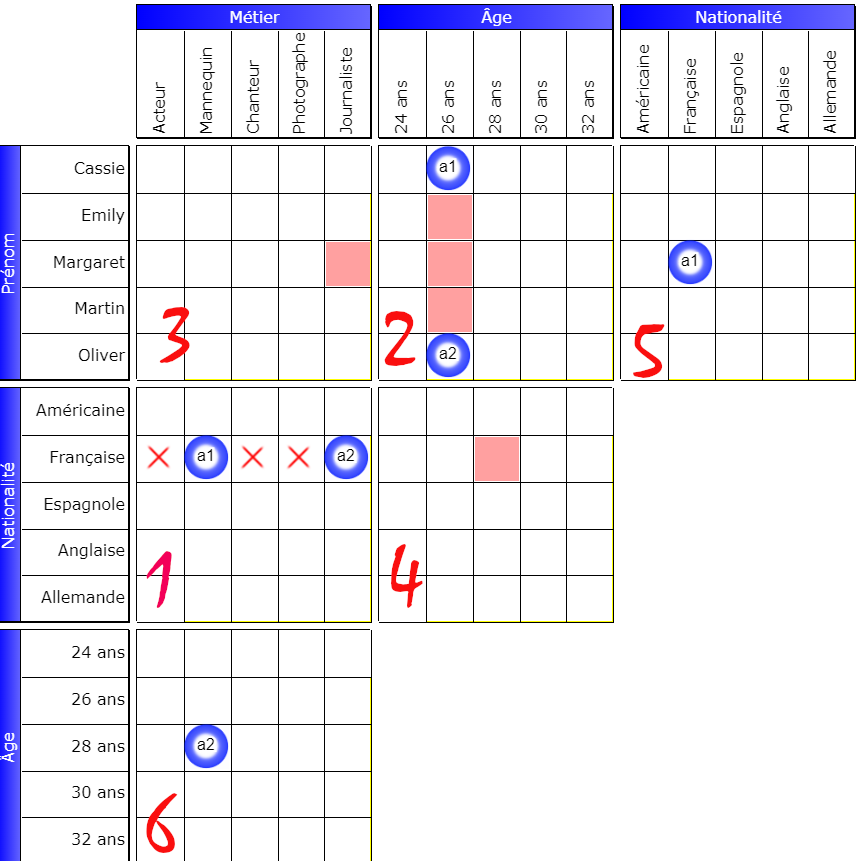
In the grid marked 1, there is an alternative: the French person is either a model or a journalist, which is materialized by the booleans a1 and a2. We therefore have a1 ≠ a2 .
Booleans a1 and a2 are scattered across the other grids.
In grid 2 we see that all the boxes at the intersection of a1 and a2 are false. This is normal since a1 and a2 form an alternative defined in grid 1.
Things are more subtle in grid 3 and grid 4. Let’s apply the merging techniques.
In grid 3, Margaret cannot be a journalist. If we merge the row containing a1 in grid 5 with the column containing a2 in grid 1, we discover that a1 = a2. However, since a1 ≠ a2, the merge is not possible and therefore the pivot cell (Margaret, journalist) is false.
In grid 4 , the French guest cannot be 28 years old. Let’s merge the row containing a2 from grid 6 (row 28 years old ) with the row containing a1 from grid 1 ( French row) . Here again a1=a2 which is not possible and therefore, the pivot box (French, 28 years old) is false.
It’s the same principle with the following riddle:

Still applying the fusion techniques, we discover that the pivot boxes (Cassie, Actor) and (Margaret, Photographer) are necessarily false.
To easily spot these cases, look at the rows containing the same Booleans, identify the common headings, and find the pivots: here the common heading is French (“Française”).
Hard, hard… a little invariance
There are cases of intersection that are more difficult to find. Consider the grid below, taken from the “orchard” puzzle. I’ve emptied all the boxes except those relevant to my purpose.
These intersection cases actually fall under invariance, an advanced technique that is described in another chapter. But this is a very simple case of invariance, which is why the solver is able to reveal it by processing intersections, when dealing with alternatives of two Booleans.
Look at the grid below.
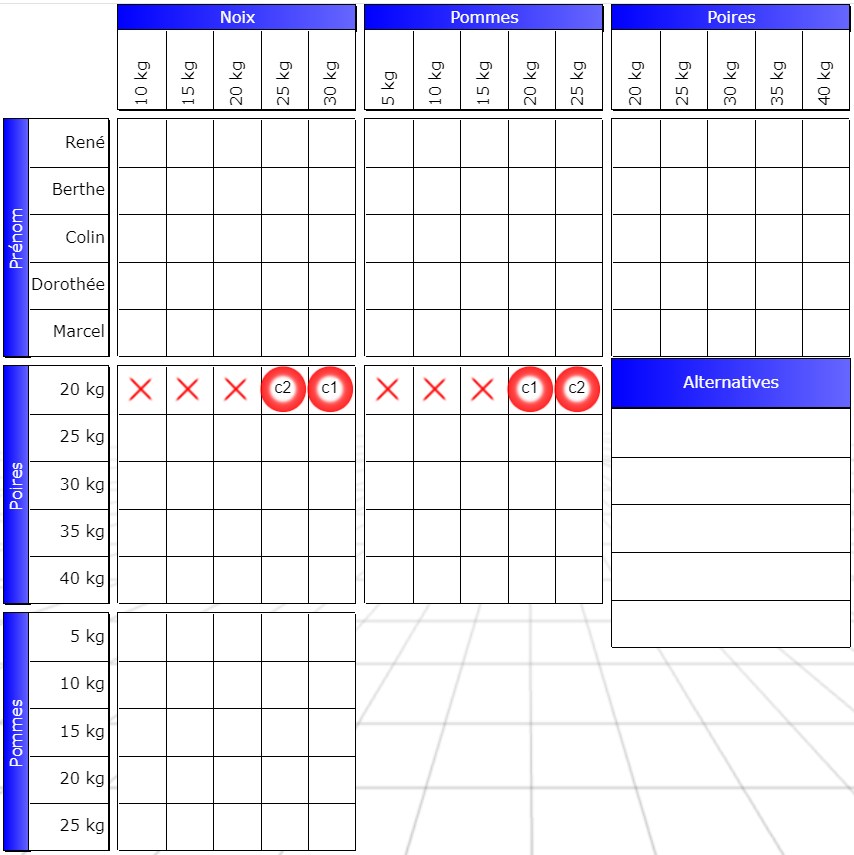
There are two boxes that are always false. Do you see them?
To find them, simply ask yourself what happens if c1 is true, then what happens if c2 is true. We then discover two boxes that are always false. If you haven’t found them, take a little time to discover them before reading on.
Here is the answer:
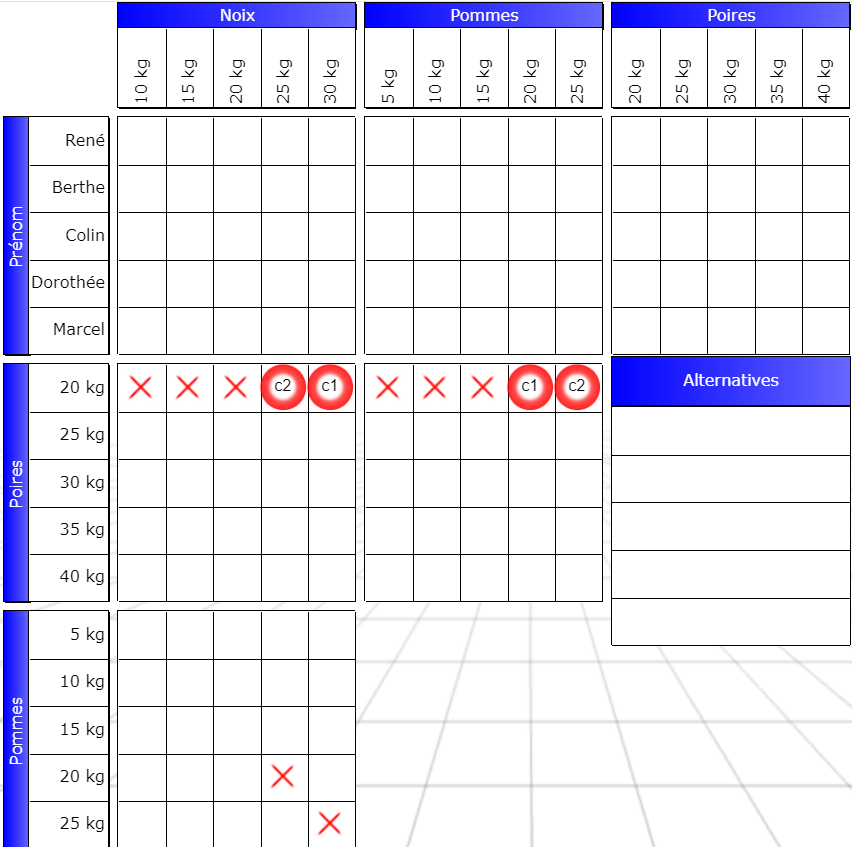
There’s an easier way to discover these squares. Using intersection, that is.
First, note that c1 and c2 are alternatives. One is true, the other is false. Instead of reporting the true signs in the bottom “apples” (“pommes”) grid, let’s report the Booleans c1 and c2 , depending on whether one or the other is true. If c1 is true, it will be true in the “apples, 20kg” row . If c2 is true, it will be true in the “apples, 25kg” row .
Here we only reproduce the bottom of the grid:
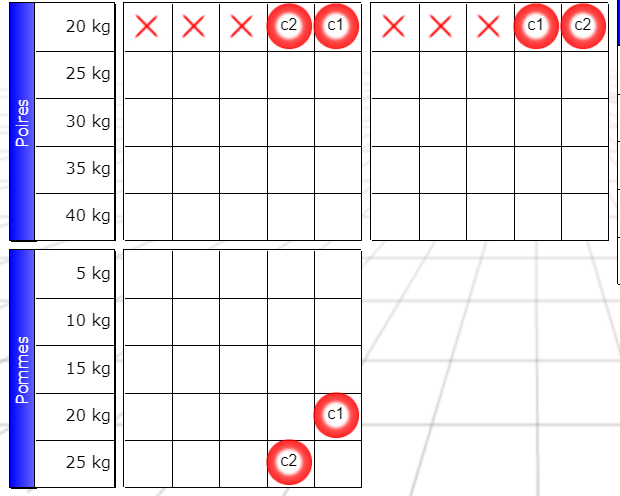
This is a form of repercussion that we have not yet studied.
Now we just need to apply the intersection to them:
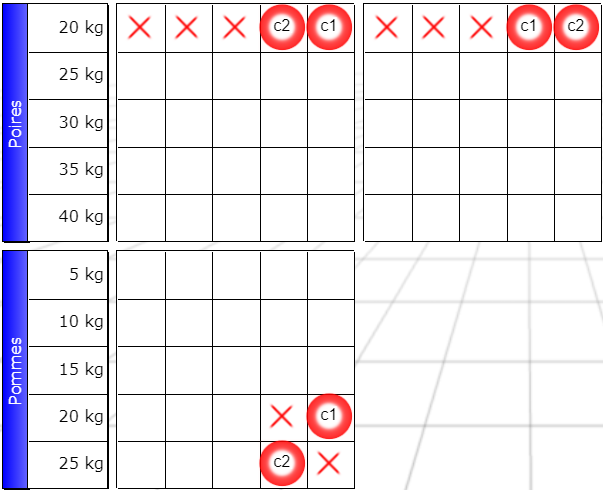
You can leave both Booleans in place. The solver doesn’t: it just puts the false signs in place, without passing on the Booleans.
