As with addition, the examples presented in this article involve numbers greater than 100. It is of course possible to use dominoes with numbers less than 100.

Subtraction

Subtraction is not commutative: a – b ≠ b – a. The operand a is the one from which we will subtract the value b . If we use dominoes to do a subtraction, we obviously need two bars. We will place the value a in the top bar.

Let’s perform the following subtraction: 523 – 345

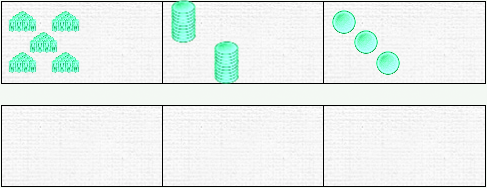
To perform the subtraction, we will remove 345 tokens from the top bar and transfer them to the bottom bar. As with addition, whatever remains in the top bar will be the result. The initial value a is therefore destroyed and the value b is found in the bottom bar.

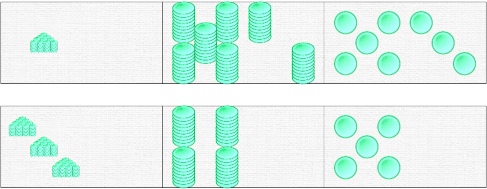
There’s no major difficulty in performing the calculation with the dominoes. We’ll remove tokens to form the value 345 at the bottom, ensuring that there are no 10 tokens in a domino. The student’s task is therefore to write 345 on the bottom dominoes using the tokens available on the top dominoes, making the necessary conversions, and then to read the result from the top bar. Before reading the result, make sure that all passages have been made. The order in which the passages are made is irrelevant, and the student performs no calculations.

So much for dominoes. Now let’s review the two most common operating techniques.

Two common subtraction techniques

The operating technique is a convention; for a long time, French schools taught only the technique known as “conservation des écarts” (gaps conservation). It’s a bit complicated, but it’s compact, and that’s probably why it was chosen. But the truth is, few students understand it. For years, they learned the technique mechanically, applied it to find the right result and that was enough – teachers didn’t ask for more. The good student applied the technique in the same way as he recited his lessons by heart. He wasn’t asked to understand, just to reproduce.

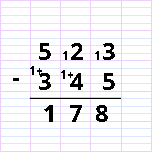
NB: In the most traditional method, we do not write the “+” after the 1 that we add in the middle line. This creates a little confusion.

The other Anglo-Saxon technique is called “exchanging.” It has the advantage of being easier to understand, but perhaps requires a little more care in writing. There are some variations in the representation of this method.

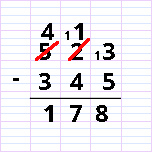
As you can see, the exchanging method is much closer to what can be achieved with decimal dominoes.

Using decimal numbered dominoes: from passing to exchanging

First, let’s prepare the ground: write the operation to be performed and place the first number in the top dominoes.

As with addition, we will first deal with the units, then the tens, then the hundreds.

A detailed example on units

We need to place 5 tokens in the bottom ones domino. We can already transfer the first three. Then, as usual, we’ll take a pile from the tens domino and transfer it to the top ones domino. Finally, we transfer two more tokens to the bottom ones domino.

Here is a short summary of the 3 steps of this manipulation:

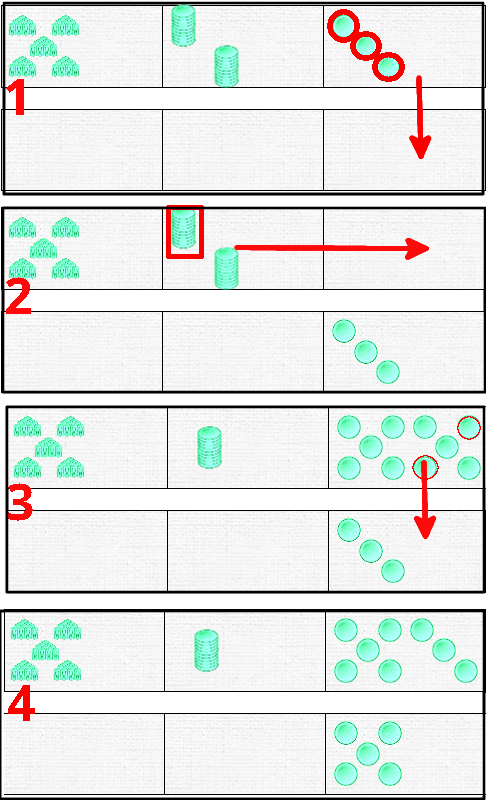
Normally, if the students have had time to manipulate the dominoes, this sequence of actions should pose no problem. Now let’s see what happens with our operation.

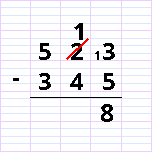
Let’s tell the students right away that our written operation is going to be different from what happens with dominoes.

The first difference with dominoes is that we’re not going to proceed unit by unit. That would take far too long! So we’re going to try subtraction, find that 3 is too small compared to 5 – using the time-honored formula: “three minus five, we can’t”, and pass the ten. “I’m borrowing a ten – there’s one left”. We place the 1 above the 2-tenner and write the small 1 in front of the 3. This is where we need to explain: it corresponds to the ten chips we’ve transferred to the domino. By adding 10 units to the three already there, we get 13 – which is the same as writing “1” in front of the 3. This is the second difference with the domino, which cannot contain 13 tokens.

Then, of course, we calculate 13-5 and mark the result. We see that this is indeed what appears in the top units domino.

Thanks to the decimal numbering system, students should have no difficulty understanding the tens passages. We can emphasize the operational differences between the domino and the exchaning technique, but not the passage itself, which has been seen and reviewed during counting and addition.

Now just continue with the tens, alternating between working with dominoes and representation.