How to use decimal dominoes to learn tens and counting to 100.

That’s it, the pupils are counting to 10. They are used to adding and removing tokens one by one. They can count up from a pile of 5 and even create numbers by removing a few tokens, such as obtaining a 9 from a pile of 10.

Now they need to go further and understand tens. For this, the decimal domino is an interesting aid.

Dominoes “tens” and “units”

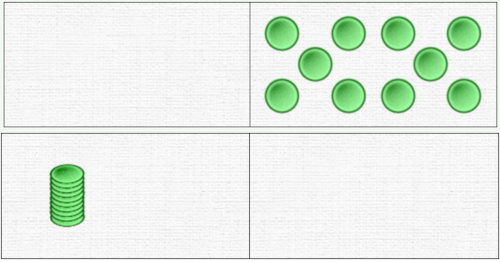
In free work, we start with a bar containing two dominoes, “tens” and “units”. Setting 1,2,1,-.

On the left we have the selector with the unit token, the stack of 10 and the stack of 5.

Once again, we use an interactive digital board: as always, the gesture is important, and must be seen, hence the importance of dramatizing the activity.

Discovering, passing on and deepening the notion of tens

It’s best to explain to the pupils in advance what we’re going to do; in new situations, it’s important to be explicit and prepare them for the novelty. So, let’s show them the worksheet above and tell them our objective: to place 11 tokens. Let’s ask them what happens if we add a token when there are already 10, to get 11, and let them express themselves a little. They’ll probably be surprised to find two dominoes side by side – explain that we’re going to use both dominoes. Chances are, they’ll suggest placing the extra unit in the second domino. Which, given the information they have, is an idea worth testing!

Let’s start the activity. Let’s create the ten by iterating the unit using the domino on the right:

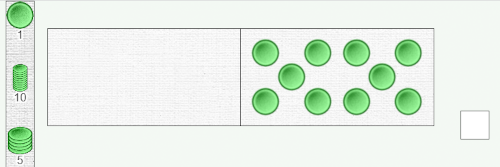
To get to 11, the pupils might suggest adding the extra token to the other domino. But before doing so, we’d better check that it isn’t actually possible to add it to our first ten tokens. So let’s try it: add a token to the ten already there and see what happens.

Impossible to place an extra token in the domino: an error tone sounds, the token goes to the small box, our waiting room. Clearly, there’s no room left in the right-hand domino for one more token.

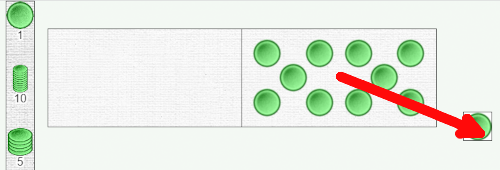
So let’s try to move the token to the left domino…

Again, it’s a categorical refusal. The token is moved to the left-hand domino, which returns to its original position.

The teacher takes the opportunity to provide some important information: the domino on the left only accepts stacks of 10 counters ! This is why the single counter is refused.

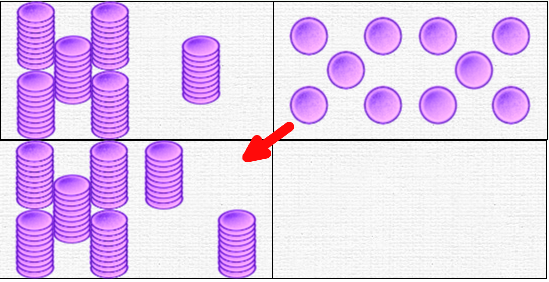
Second important piece of information: you can build a stack from 10 tokens. How does it work? The teacher grabs one of the ten chips in the right-hand domino and moves it to the left-hand domino. All the chips in the right-hand domino come together and pile up: we have a stack on the left, and nothing on the right.

The animation that occurs at this point is very important for understanding: the tokens move and stack. The stack is not a separate object: it’s the chips, but arranged differently. Don’t hesitate to repeat the animation. Replace the stack of 10 in the right-hand domino: the stack unravels and the ten chips are put away. Repeat to show how the stack is formed. There’s a similar activity that can be done without computers, with cube bars.

Video: The transition to ten.

Stack formation only works with 10 tokens. If one is missing, the token is simply rejected by the domino on the left, and returned to the waiting box. You can show this to the puils now, or let them experiment later to discover it for themselves.

Let’s return to our initial objective: how to place 11 counters. The solution then appears quite easily. We have ten in the stack, and the domino on the right is empty. So we just need to add a token: we have 11 of them: 10 on the left, 1 on the right.

To introduce the concept of ten, we still need to equate the pile of 10 tokens with the ten, which shouldn’t be too difficult: since there are ten tokens in a pile, it’s a ten, because we hear “ten” in “ten.” We will generalize this concept with other collections of objects.

To introduce the concept of ten, we still need to assimilate the stack of 10 tokens with the ten, which shouldn’t be too difficult: as there are ten tokens in a stack, it’s a ten, This concept can be generalized to other collections of objects.

At this point, pupils may be curious and eager to use the dominoes: we can let them explore. This phase is important: each student should be able to take time performing the manipulation, to fully understand and assimilate it. For this, tablets or individual computers are good allies.

Go further

Numbers up to 19

We can build each of these numbers using our dominoes, as we study them. We can certainly place the tokens one by one starting from the empty domino, but the ideal is obviously to overcount from 10. To clearly mark the transition to the ten, I suggest placing the 10 bar first in the units domino , which produces 10 counters and makes the transition to the ten obligatory, thus helping to reinforce the concept.

The number 20

… is handled like the number 10: on our two dominoes, 20 is initially represented by a ten and 10 units and we make the transition.

Numbers up to 99

…follow the same routine.

The following section is only for French students. Others are lucky enough to have “septante,” “octante,” and “nonante”!

The number 100

With two dominoes, the number 100 appears in two forms: 100 = 9 tens and 10 units, which we convert to 10 tens.

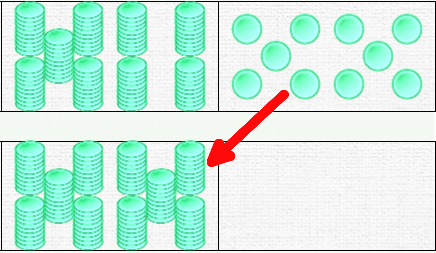
We note that we could continue and add units – up to a value of 110. But it’s better to stop there. This is the moment to bring out a third form of domino: the hundred domino! To do this, we move on to three dominoes, setting hundreds, tens, and units … and we reproduce the transition. I propose to designate the pile of stacks of 10 forming the hundred by the term “pile” or “pile of stacks,” to differentiate it from “stack.”

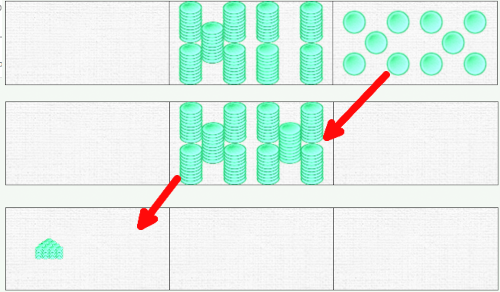
The three representations of 100 with three decimal dominoes, and passage from one to the other.

With three dominoes, we therefore have three possible representations of the number 100. The third form is the one that must be retained to write the number. See the point of vigilance below, which is valid for 10 tens as well as for 10 units.

Once you get to the hundred domino, the pile of 100s decreases a little in size; when there are several, this makes counting easier.

Beyond 100…

Always the same routine, we stop at 1000 because there are no more dominoes!

Writing the number

A point of vigilance

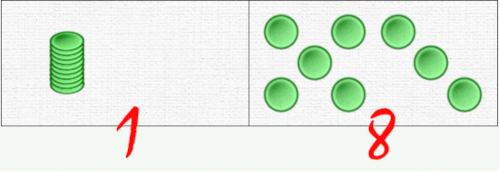
In the decimal system there are ten digits, from 0 to 9. There is only one way to represent the ten by a number: it is 10 – that is, one ten, 0 units.

But, in our decimal numbered dominoes, there are two representations:

The two ways to represent the number 10 with the “tens” and “units” dominoes

It is therefore important not to move too quickly to decimal writing, as one might be tempted to do without thinking!

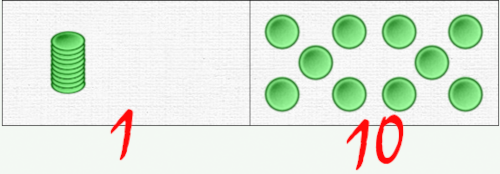
As is often the case, the easy way out is a trap!

For the record, during the development I had automated the passage of the ten. As soon as the units domino received the tenth token, the ten tokens grouped together and joined the tens domino. Finally, I abandoned the idea because it does not allow us to clearly understand that a ten = 10 units: we do not have time to see the ten tokens because they are immediately transformed into a ten. It seemed to me much more relevant to make a specific, voluntary manipulation on the part of the student mandatory.

Furthermore, mathematically the following formula is correct: 20 = 1 ten + 10 units. Our students should be aware of this, and for this, we can count the tokens.

Of course, this remark is also valid in the case of the number 100, with 10 tens.

The special status of the 10 domino

Notwithstanding the cautionary point described above, the writing of the number follows naturally from the arrangement of the tens and units in the domino. But a little additional explanation may be useful to explain that 1 ten and 10 units is 20 and not 110.

In the decimal system there are ten signs to designate the numbers: 0 to 9. We can associate the first configurations of our domino units with a digit.

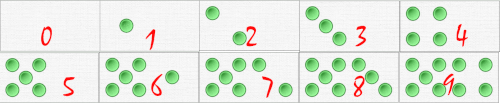
A digital strip like this can be posted in the classroom.

We see here that we are simply associating the conventional representation of the domino with another conventional representation, the digits. Students should be familiar with this representation of dominoes. There is a different number, and only one, to designate each of these dominoes.

What happens to domino 10?

We no longer have a digit to represent this domino. The stock is exhausted! The only way to represent it is the number 10. But this number is made up of two digits, 1 and 0. How can we do this? This is where the passage with our two dominoes comes in.

Writing “large” numbers without even knowing how to name them

Why not ?

Once students know how to handle dominoes and write the numbers from 0 to 9, we can very well offer them the following activity: using dominoes to write numbers (less than 100 all the same) without even having studied them. It’s up to the teacher to name the number.

Here are two cases; the second requires intermediate manipulation.

6 tens and 10 units = 7 tens and 0 units = 70

Digital tables

At this point, the table can be used to write the number of tens and units. The table allows students to understand the logic behind writing decimal numbers and enables them to write some simple equalities. “Tens” and “units” can be abbreviated as “t” and “u.” Note that the boxes “100’s,” “10’s” and “1’s” do not designate the digits of hundreds, tens, and units, but the number of hundreds, tens, and units. This point is fundamental. If it is not understood, many errors are likely to occur, and it is impossible to understand numbers described as “5 tens and 18 units.”

70 :

10’s	1’s
6	10
7	0

As you can see, we write 10 units in the “u” column if the domino has it, but we add a second row for the conversion. This prepares students for more complex equivalences, which we can tackle when 100 is exceeded: for example, 15 tens = 1 hundred and 5 tens. This also prepares them for the transfer of carryover in additions.

When we get to 100, we will use the three-column table, with the hundreds “c”. It’s exactly the same principle. The three-story representation of 100 seen above can therefore be written as follows:
100 :

100’s	10’s	1’s
0	9	10
0	10	0
1	0	0

Conversions between units, tens, hundreds

To study conversions, we can transpose statements involving the decomposition of a number into dominoes. This is already a complex case; it is recommended to start with a simpler example.

Write the number corresponding to :

100’s 10’s 1’s

4 16 14

The student can manage dominoes quite easily.

The most immediate way is to use a bar of 3 dominoes and place each element one by one, grouping the stacksof 10 towards the higher power of 10. This requires careful counting, but the method is simple to implement.

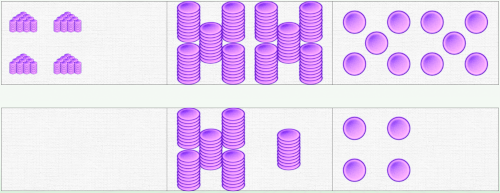
Another method uses two domino bars, but it only works with certain statements: you must not exceed 20 tens and 20 units, which is the case here. It allows you to better check the number of pieces placed.

The student begins by placing all the pieces, counting the elements in the corresponding top and bottom domino.

His goal is to group all the pieces into a single bar. He doesn’t have to follow any particular order, but he must take into account size constraints—10 elements maximum per domino, which still requires sequencing his actions correctly. He will have to group the ten tens from the top bar into a hundred, and the ten units into a ten. He must also add the other chips and check that there are no more dominoes with 10 elements (we will avoid reaching 10 hundreds).

In the end, he gets this, which is the answer. All that’s left is to write it in numbers: 574

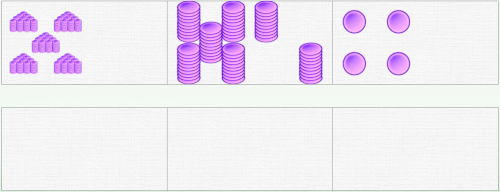
Of course, you can start conversions with just tens and units.

The rule
To write a number from decimal dominoes, you must first complete all the passes.

Only then can we count the number of hundreds, tens and units.