Learning to count, discovering numbers: the decimal number domino can provide a visual aid to this learning process. This article explains the pedagogical principles behind this tool and suggests a few activities.

Warning

The teaching guidelines given here are general. Whether you use them with dominoes or not, you can apply them to all other counting situations.

The decimal domino described here is one of the activities that can be proposed to pupils, among others, in kindergarten up to at least first grade. Activities should be modulated according to the age of the children, and should not be rushed. Parents, don’t rush things – it can be detrimental!

The different aspects of a number

The nominal aspect

These are the signs, graphic or sound, that we use to represent a number. The sign 7 is written in English as “seven” and is pronounced /ˈsɛv^ən/, /ˈsɛvən/ or /sev′ən/, according to the country. The nominal aspect depends on local conventions and the language used – for example in Burmese it is written as ၇.

There are many possible representations. The domino below is another conventional representation of the number 7.

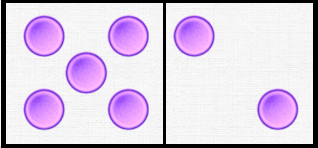The cardinal aspect

This is the most common aspect: a number is used to represent a quantity of elements in a set.

There are 7 bikes under the courtyard.

The ordinal aspect

It is quite easy to understand this aspect when studying a language and learning the ordinal numeral adjectives: first, second, third, fourth… When learning to count, we often simplify by replacing the numeral adjectives with their nouns: one, two, three, four…, thus using the number rhyme. The ordinal aspect is therefore the position of an element in an ordered series of elements where each element has an order number.

Counting: numbering and enumeration

Counting involves all three aspects described above. The nominal aspect is when a sign is used to identify the number—whether that sign is a digit, a written word, or a spoken word. The cardinal aspect is when the quantity of elements is found—the cardinal of the set. The ordinal aspect is in the strategy used to count. Indeed, to count, you have to order a series, even if the elements that compose it are all identical and placed haphazardly. If I have to count the number of marbles in a bag, I can take them out one by one and place them in a container, thus creating an artificial order and taking advantage of this action to count them. The same goes for the tokens of our dominoes.

We distinguish between counting-enumeration and counting-numbering (Rémi Brissiaud).

Counting-numbering is commonly used in families. Objects are pointed out one by one and numbered. The number rhyme is recited and then stopped at the last object – the last number expressing the number of objects. However, this creates a shift in meaning, from numbering an object to expressing a quantity of objects. When this is done, young children do not associate the number spoken with the quantity of objects in the collection, but with the object being counted itself . This can create significant problems in understanding number.

To correctly assimilate the measurement of quantity, it is important to proceed by counting-enumeration, by iteration of the unit.

Decimal number dominoes and iterative counting

The decimal-numbering domino is just one of the tools you can use to learn to count. It should not be the only tool, of course, and should not replace the manipulation of real objects. However, its automation can be used to vary teaching by adding a visual “extra”: the automatic movement of the tokens in the domino. Ideally, you should use an interactive digital board rather than a simple video-projector, because the gesture is very important, it’s part of the counting procedure, and for that it needs to be seen: it needs to be dramatized. If we’re lucky enough to have one, we’ll reserve the tablets for individual or small-group work.

Settings: free work, “unit” mode and a single bar ( 1,1,1,-)

You can place tokens one by one into the displayed domino. Notice the selector on the left: it contains a unit token, but also a stack of 10 tokens and a stack of 5. We’ll come back to this.

Let’s use counting-enumeration technique. Here is a possible example of how to present the activity.

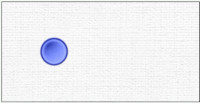
Let’s place the first token. Take it from the selector, move it to the domino, then say “There is one token.”

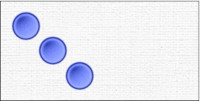
Take another token from the selector, move it, and drop it into the domino. Then, say “and another… 2.” Note that ” and another ” can be said when you take the token from the selector. But to say the 2, you have to wait until the token has found its place in the domino (important). By doing this, you make it clear that it is not the “two” (cardinal) token that you are taking, but the second (ordinal) one; the moved token is assimilated to the unit (” and another “).

Continue with “and another… 3”. And so on.

In doing so, we describe the action of adding the token to the domino, as well as the result of the operation (the cardinality of the set) in a single, very simple sentence.

Of course, we’ll stop counting based on the children’s ages. For little ones (3-4 years old), going up to 3 or 4 is great!

The three ways of representing tokens in dominoes

Standard mode, with a classic representation of numbers in two parts of 5.

The “columns” mode where the numbers are distributed two by two, from top to bottom, in 5 columns.

Finally, the random mode, where the ten positions are chosen at random, can be clicked multiple times; this changes the arrangement of the tokens each time.

When using two domino bars, only the top bar is affected by the mode change. The bottom bar remains in standard mode.

Organized or random positions

By using the positions of the tokens in the standard mode, students will eventually identify numbers by the positioning of the domino tokens, which is always the same for a given number. This is normal and is one of the advantages of computerized dominoes. Each time a token is placed or removed, the others rearrange themselves to form the classic domino figures in decimal numbering. Ultimately, recognizing a figure improves counting because it makes overcounting easier . Overcounting is the act of counting by starting the enumeration with a known number greater than 1.

Normally, for 1, 2, 3 and sometimes 4 tokens, the brain should be able to conceive of the number without having to count. Here the position of the tokens in the domino is not important. But from 4, the organization becomes useful for overcounting. This ability of the human brain to recognize small quantities is called ” subitizing “. Caution: this does not exempt you from learning to count by iterating the unit from 1. Just because the child recognizes the quantity “3” does not mean that he knows how to count and has acquired the notion of number.

Counting in this way and associating an arrangement with a number enables the child to acquire the conviction that the arrangement summarizes the counting of the whole; it is no longer necessary to count from the unit.

Counting and changing the position of tokens

This activity is more interesting from numbers 4 or 5, since numbers up to 3 are recognized without counting. But of course, nothing prevents you from practicing it on smaller numbers.

Settings: free work, “unit”, two bars and standard mode (1,1,2,-) .

Start the counting activity as described above on the top bar. Stop when you reach a target number, for example, 5. Here, change the standard mode to “columns” mode or “random” mode. The arrangement of the tokens changes to reflect the new mode (first arrow in the illustration below).

The question to ask is: “Are there still 5?” Pupils may be tempted to count without moving the pieces, by pointing at them; but to avoid counting-numbering, we can take each token one by one and move it to the bottom domino, repeating the rhyme “and another 1…” (second arrow) . The bottom domino is not affected by the change of mode and therefore displays the number 5 in a more classic and recognizable form – the one we had at the start of the game.

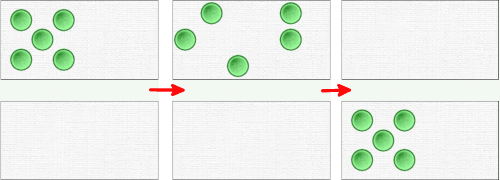
Note: There is no automatic reordering of tokens in random mode when adding or removing them.

After these masterful manipulations, pupils can explore on their own. Counting is probably more interesting to practice in pairs.

The number 5

What we’re talking about here works best in classic representation – standard mode.

The selector shows a stack of 5 tokens, which can be moved to the domino-unit in a single operation. The stack is then transformed into 5 independent tokens. A short animation shows the 5 tokens leaving the stack and moving to their own positions, providing a clear understanding of the situation.

If there’s no more room to add 5 tokens, the whole stack goes into the small box to the right of the domino. This is the “waiting room”. If you want to place the stack, you must first remove the excess tokens from the domino. So it’s best to start with an empty domino.

The stack of 5s is the starting point for counting! Apart from the fact that it’s much faster, the main benefit is to break the rythme, which starts at 1; the pupils understand that 5 is another possible starting point. “I’ll put 5, then 1, 6”. When the pupil says: “I put 5”, he takes the pile of 5 and places it in the domino. A single gesture, but 5 tokens. This further reduces the importance of counting-numbering and clarifies the notion of number as a measure of quantity.

With 5 this activity has another interest: gently preparing the basic decompositions from there: 6=5+1, 7=5+2, etc.

The countdown

Counting down begins with an initial number of tokens. Here, the stack of 5 is interesting because it allows you to start the game from an empty domino without having to count the units. To remove a token, simply move it to the area outside the domino. The token is then instantly destroyed, and the remaining tokens are reconfigured.

If you’re just starting out, it’s best to wait until pupils can orally identify a number from the arrangement of the tokens. That’s why I think the classic mode is necessary here, at least at the beginning.

This time the rhyme becomes: ‘I put in 5’, ‘I take out 1, 4′, and so on. The fact that pupils recognize the classic arrangement of the tokens can help them with this task. If they don’t know the number sequence, they may tend to recount the remaining tokens from 1. Hence the importance of recognizing an arrangement and associating it with a number. In my opinion, if they recount, it’s better to postpone the activity and train them in incremental counting in standard mode.

For students who are very successful at counting backwards in standard mode, it may be interesting to repeat the game in random mode. There, there is no longer any recognition of the number by the arrangement of the tokens! The memory of the numerical sequence is mobilized, with perhaps a little recounting to be tolerate here, in case of hesitation – possibly using two bars to facilitate counting (setting 1,1,2,-).

Of course, this activity can be adapted to suit the age and ability of the pupils. Other activities involving one or two unit dominoes are possible; it’s up to each individual to adapt this tool to his or her class.

The number 10

If working with a single domino, the number 10 cannot be exceeded.

The stack of 10, in the selector, allows you to place 10 tokens at once, provided the domino is empty.

Using the stack is useful when counting backwards from here. But it can also be used, like the stack of 5, to quickly create certain numbers.

Placing quantities of tokens

A target number is set, different ways of reaching it are identified, and an attempt is made to determine the most efficient one (i.e. the most economical in terms of moving tokens).

The classic procedure, which has been used since the beginning, consists of placing the tokens one by one until the target number is reached. If the target number is greater than 5, the trained pupil will over-count, using the stack of 5. To obtain 9 tokens, the most efficient procedure known at the moment is to place the stack of 5 tokens and iteratively count up to 9, i.e. 5 manipulations. That’s 5 manipulations.

But we know that to place 9 tokens, it’s more efficient to place 10 and remove 1! The same goes for obtaining 4 from a pile of 5.

This activity is particularly rich in terms of learning, as we reinforce the notion of numbers by looking for the quickest way to obtain them. What’s more, in a small way, we’re introducing (but not naming) subtraction.

And reading the number?

As you can see, in free-work mode, the number is only displayed in the form of dominoes. Numbers are not displayed. This is deliberate. The aim here is to focus on manual, visual (by arranging the tokens) and oral (numerical counting) learning. Adult support is therefore necessary, at least initially. Reading numbers is not covered here. Teachers are free to supplement this as required. The construction exercises in the other menus can only be used if the student can read at least the first ten numbers.