Introduction to Booleans

A Boolean is a two-state variable, which is generally assigned the values ​​true or false. In a zebra puzzle, the use of Booleans allows us to identify boxes whose behavior follows the same rules: the boxes identified by the same Boolean are either all true or all false. Thanks to them, a statement can be coded directly in the grids. Once the statement is entered, there is no need to return to it. Most zebra puzzle statements can be coded using Booleans: as soon as a statement is precise, it can be coded with Booleans. Imprecise statements do not allow immediate coding. In the grid below:

• Enzo arrived 2 minutes before Océane is a precise statement
• Enzo arrived before Océane is imprecise. To code it, you have to return to the statement several times, at different stages of the resolution.

When solving a puzzle in a magazine, to represent a Boolean, you can write a letter in boxes. There are 26 letters in the alphabet, which is more than enough. For example, here’s a way to code the following proposition in the puzzle “Jogging on the Beach” as if it appeared in a magazine:

Enzo arrived 2 minutes before Océane.

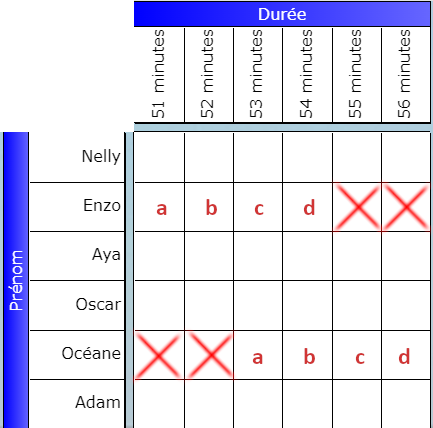
This coding establishes the order relationships between the boxes in the Enzo line and the Océane line . If Enzo runs for 51 minutes, then Océane runs for 53 minutes – this is the Boolean a. The same applies to the other Booleans. We also see that some values ​​are not possible and are represented by the false sign (the cross).

This coding with letters taken from the alphabet works well on paper where the boxes are small.

On the Actilud website, however, I chose a different representation. Each Boolean is formed by a letter and a number, and each letter is associated with a color. Booleans are displayed as colored dots:

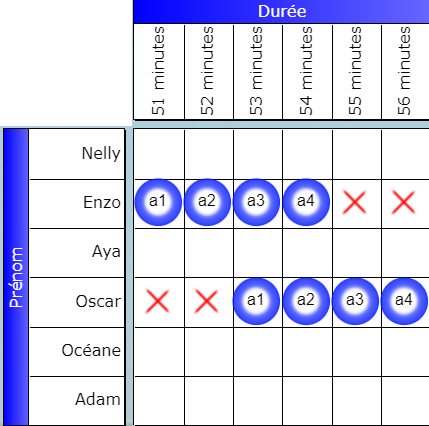
The previous coding with the booleans {a, b, c, d} here becomes {a1, a2, a3, a4}.

The advantage is to increase the overall readability of the grid. Indeed, using the same letter associated with different numbers for a given proposition makes it easy to identify the Booleans that fall under this proposition, since each letter is associated with a given color, here blue, which makes it obvious at a glance. But, from a purely logical point of view, the two representations are strictly equivalent.

Basic Mathematical Rules

We will need to know the basic rules of Boolean algebra. These rules are quite intuitive. Let a and b be two Booleans.

Rule of and

(a and b) is true only if a is true and b is true. In all other cases (a and b) is false.

a→ b↓	FALSE	TRUE
FALSE	FALSE	FALSE
TRUE	FALSE	TRUE

This rule is cited for the record. We use it implicitly in integrams. Let us take the riddle “kites”. The statement formed by the compound proposition Sandra plays for 30 minutes and has a blue kite is true only if the two elements that constitute it, Sandra plays for 30 minutes and Sandra has a blue kite , are true. Now, since by principle the statements are true , the constituent elements are therefore always true.

Exclusive or rule ( or )

(a or b) is true only if one of the two Booleans is true. In particular, (a or b) is false if both a and b are false or true.

This rule is very widely used in integrams; it establishes the alternatives.

a→ b↓	FALSE	TRUE
FALSE	FALSE	TRUE
TRUE	TRUE	FALSE

If both a and b are true, either (a or b) is false. This is certainly true in alternatives. The chapter on alternatives is entirely devoted to this rule, so we won’t dwell on it. Let’s take a simple example to understand:

Nelly flies her kite for 30 minutes or 50 minutes.

We can clearly see that Nelly cannot drive for both 30 and 50 minutes. Only one of these two possibilities is correct. This is a typical case of exclusive or. Exclusive or can be translated by the phrase: either…, either…, but at the cost of a certain heaviness in the sentence:

Nelly flies a kite for either 30 minutes or 50 minutes.

The expression or often takes on the mathematical meaning of exclusive or. 

Here is the associated video (in French for instance) ; if it doesn’t appear, refresh the page.