Alternatives are the starting point for many techniques. This section does not cover any specific technique, but explains the principle of the alternative, which will be reused in specific techniques.
In a statement, alternatives are mutually exclusive propositions.
Simple case: in a grid
Alice wears a blue, red or green swimsuit.
The expression or corresponds to the exclusive or of mathematics: Alice wears either the blue jersey, or the red one, or the green one, but she does not wear multiple colors. Nor does she wear the other colors present in the grid.
Reporting this statement in a grid is very simple:

Simply complete the row with false signs in the boxes that are ignored.
Complex case: on several grids
But an alternative can also relate to several grids:
The first is either Bob or the red jersey.
Let’s analyze this sentence. Bob cannot wear a red jersey. Indeed, if Bob is first, then he cannot wear red. But if he is not first, then the red jersey wins, and so again Bob cannot wear red.
To encode this situation in a grid, we need booleans.
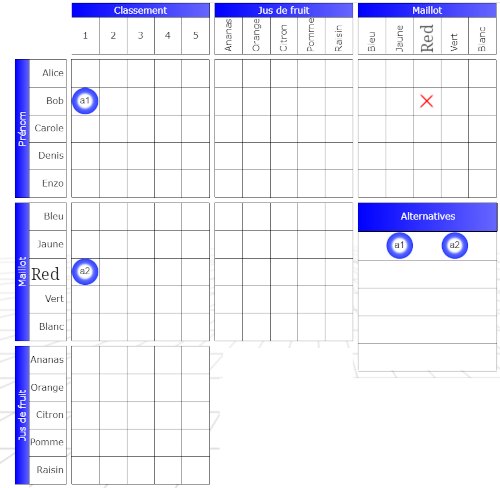
We need two different Booleans, for example a1 and a2 . To code the alternative, we place a1 at the intersection (Bob, 1) and a2 at the intersection (Red, 1). If we were working with a pencil and eraser, we would note in a corner of our paper that a1 and a2 form an alternative. On the site, we place a1 and a2 in the alternatives grid, in the same row, to indicate the alternative to the solver.
To consider that two Booleans form an alternative is to assert that:
- if one is true, the other is false,
- they can’t both be true,
- they can’t both be wrong.
And we place the false sign at the intersection of (Bob, Red) because we know that Bob is not wearing a red jersey.
Generally speaking, an alternative can involve more than two terms. In fact, multi-term alternatives are very numerous in zebra puzzles and can be generated by all sorts of statements. In this case, only one term (a Boolean) is true, all the others are false.
The solver removes alternatives from the alternatives grid
When it realizes that an alternative from the alternatives grid is found in the zebra puzzle, the solver removes it because it is no longer necessary to keep it.
Generalization
In reality, an alternative occurs when a row contains no true cells. Indeed, even a completely empty row is an alternative, since by construction, only one cell in the row must be true. But this doesn’t get us very far. Better to use Booleans; empty cells don’t contain enough information.
So let’s look at a case of alternatives coded with booleans, from a statement.
Let’s take a proposition from the fashion show, on Actilud and see how to code it:
Cassie is 4 years younger than the model.

We use the Booleans a1, a2 , and a3 to code the situation. We note in passing that Cassie cannot be a model. We distribute the Booleans according to the model’s and Cassie’s ages. We obtain two rows each containing three Booleans and two false signs: a1, a2, and a3 form an alternative.
It is not necessary to place them in the grid of alternatives: in fact, the simple fact of appearing in the same grid, on a row with two false signs, therefore without any empty box , is the signature of a three-term alternative.
Note that if there were one or two empty cells in the row containing a1, a2, or a3, these Booleans would not form an alternative. If that empty cell contained the true sign, then all three would be false!
There is an alternative when a row of n boxes contains b different booleans and p false boxes, with b+p=n.
Put more simply: in a row, as soon as there are Booleans with false signs, without any empty boxes, then there is an alternative:
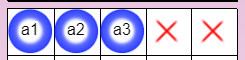
Alternatives are fundamental to solving zebra puzzles. To convince yourself, see the other techniques presented after this one.
Special cases
Alternative formed by a single Boolean
This never happens in a statement! but a multi-Boolean alternative gradually shrinks, until it contains only one Boolean.
When an alternative contains only one boolean, that boolean is considered true.
Alternative within an alternative
This is a nice case that rarely happens but which allows us to move more quickly towards the solution.
If we have an alternative [a,b,c,d] and over time we discover an alternative [a,b] on the grid, this means that c and d are false!
Video
The video below shows how the Booleans a1 and a2 react depending on the player’s action, when they are declared as forming an alternative (presence in the alternatives grid): when one is false, the other is true.
