Available in the Logic Puzzles section, the game Admission to the Gorgias Academy combines reading with logic. To solve the riddles, you need to read the statement carefully and, above all, analyze the propositions made and rank them according to the number of liars.
The principle
The player lives in Greece in 450 BC. He wishes to enter the Gorgias Academy, where Logic, among other things, is taught. He takes an entrance exam. In each examination room, his teachers, the academicians, ask him to choose a numbered ball and place it in an urn. Only one of these balls allows the player to advance in the game. The others lead to failure.
The player has two indications:
- the number of liars, indicated in the statement
- the academicians’ proposals
Some of these statements are true and others are false. The number of false statements corresponds to the number of liars. To get out of this situation, the player must:
- classify academicians into liars and “truthful,” placing them in the “true” zone and the “false” zone.
- find the correct numbered ball and place it in the urn
If both conditions are met, the player advances to a new room, containing one more academician. If he fails, he loses a point and starts again in the same room. The game stops when the points run out; however, there are still more than enough to move forward without worry.
A few historical notes
Gorgias lived to a ripe old age (108), and was in his thirties in 450 BC, the date of our enigma. Although he probably never founded an academy, he had many students who paid dearly for his teaching of rhetoric. In his treatise on non-being, he demonstrates, or attempts to demonstrate, through logical reasoning, that there is no possible ontology, which was obviously not to Plato’s taste, who widely denigrated him and with him all sophistry.
If you look at the academicians, who are drawn at random, you’ll see that there are men, of course, but there are also women. Of course, there’s no respect for historical truth here! It’s an adjustment to contemporary realities!
Truth, lies and injunction
If we analyze what the academics have to say, we discover that they are of two kinds.
- the propositions: “Ball 2 brings failure”
- injunctions, which are not, strictly speaking, propositions: “Don’t choose ball 3!”
A proposition, in logic, is a statement that can be true or false. However, an injunction is not a proposition; it is an order that, a priori, cannot be true or false. However, if we read the introductory statement carefully, we know that we must “divide the academics between liars, who wish the player to fail , and those who tell the truth, who wish him to succeed .”
In general, there’s an independence between the will to help or harm, and the will to tell the truth or lie. In fact, you could imagine a puzzle where it’s the liars who want to help the player! So the introductory sentence is extremely important, because it’s the one that establishes whether the injunctions are true or false.
Why did I include injunctions? Quite simply to vary the reading experience (just a little).
If you have students, it’s important to make sure they understand the role of introductions in logic problems.
Two levels of interpretation
To make the analysis a little more challenging, you can select the “difficult” level in the sentence interpretation settings. In this difficulty level, some academics refer to the words of other academics. We then have to transform their words to solve them.
Alpha says, “I agree with Omicron.”
Omicron says, “Choose the 5 ball!”
We need to transform Alpha’s proposition. He agrees with Omicron, so this means he is saying the same thing as Omicron: “Choose ball 5!” We can then apply a truth or lie status to these propositions.
Alpha says: “I agree with Omicron” ⇒ “Choose ball 5!”.
Omicron says: “Choose ball 5!”
Here is another case:
Alpha says, “Don’t listen to Omicron!”
Omicron says, “Don’t choose the 3 ball!”
Here Alpha disagrees with Omicron. In fact, he recommends not listening to him. So we must say the opposite of Omicron . After transformation, this gives:
Alpha says: “Don’t listen to Omicron!” ⇒ “Choose ball 3!”
Omicron says: “Don’t choose ball 3!”
Finding the “truthful” and the liars: Staying consistent
This is the most interesting part of our puzzle. Initially, all the academics are placed in the “truthful” zone: ![]() . The liars’ zone,
. The liars’ zone, ![]() , is empty.
, is empty.
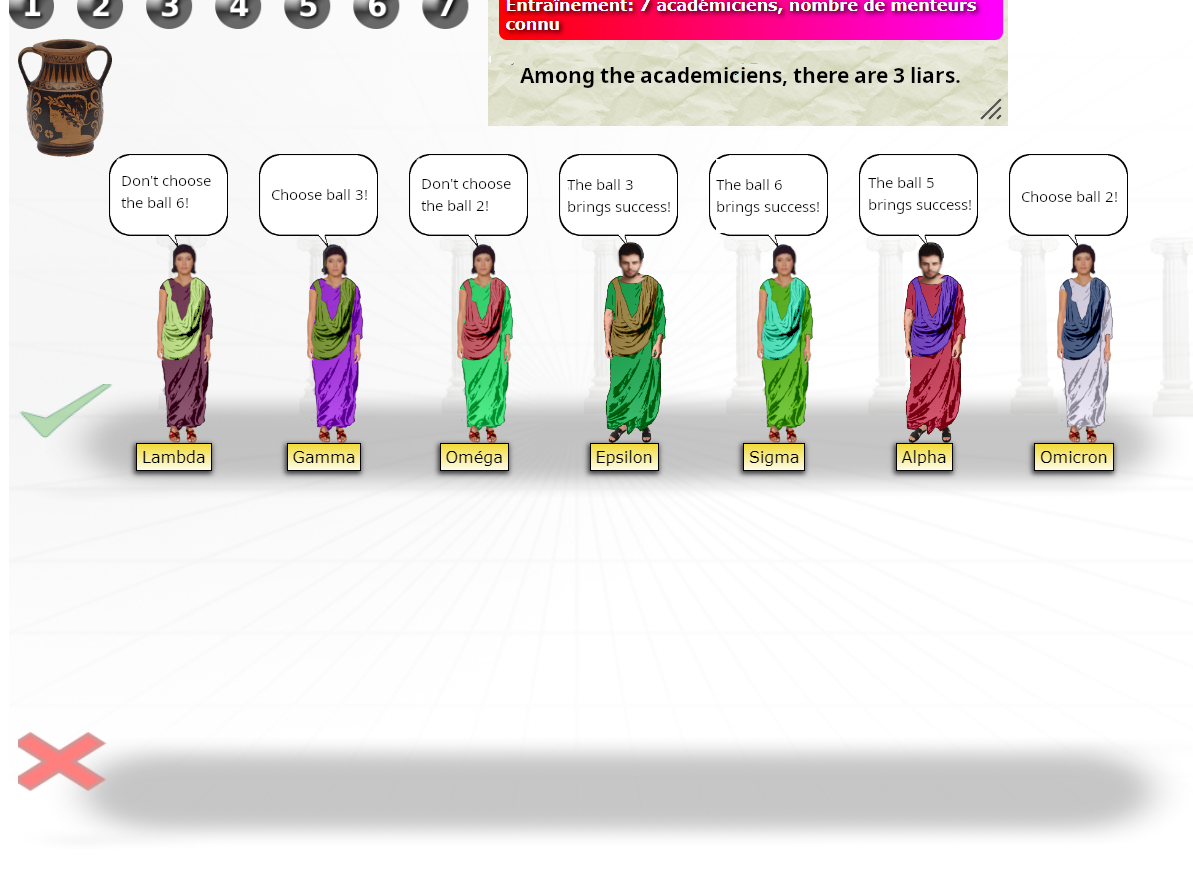
In the illustration, there are three liars. So we need to move three academics into the area ![]() . But how do we do this? By making the statement coherent .
. But how do we do this? By making the statement coherent .
Consistency is key
From the introductory statement we know three things:
- there is a solution
- This solution is unique
- there are three liars
There is a solution, so we can solve the puzzle and we can reject an answer that does not offer any “winning” balls.
The solution is unique, so we must reject any answers that produce multiple “winning” balls.
There are three liars: so three academics are needed in the lower area.
How can the statement be made coherent? By grouping together the statements that talk about the same ball and reversing the liars’ propositions.
Reverse the propositions
Here’s how it goes for the second academician, Gamma:
She says, “Choose ball 3!” which translates to, “Ball 3 brings success!”
If she lies, her guess becomes, “Ball 3 brings failure!”
Group together statements that talk about the same ball
We see by carefully observing the puzzle above, that there is a problem with ball 2.
Omega: “Don’t choose ball 2!” ⇒ “Ball 2 brings failure.”
Omicron: “Choose ball 2!” ⇒ “Ball 2 brings success.”
One of them is lying, of course.
If Omega is the liar, then Omicron is telling the truth. So ball 2 leads to success. But the statement also indicates that ball 3, ball 5, and ball 6 lead to success. Now, we know that there can only be one ball. If we maintain that Omega is a liar, there must be 5 liars for the solution to be coherent: “Ball 3 brings success” (two liars), “Ball 6 brings success,” “Ball 5 brings success,” and of course, “Do not choose ball 2.” However, this number of liars does not correspond to the statement: 3 are required. We can therefore say with certainty that Omega is telling the truth and that Omicron is one of the liars.
One thing leads to another, and by moving the figurines around the zones, we end up with a coherent solution: the liars are the last three (Sigma, Alpha, Omicron). The result is a single piece of advice, given by two academicians: choose the 3-ball.
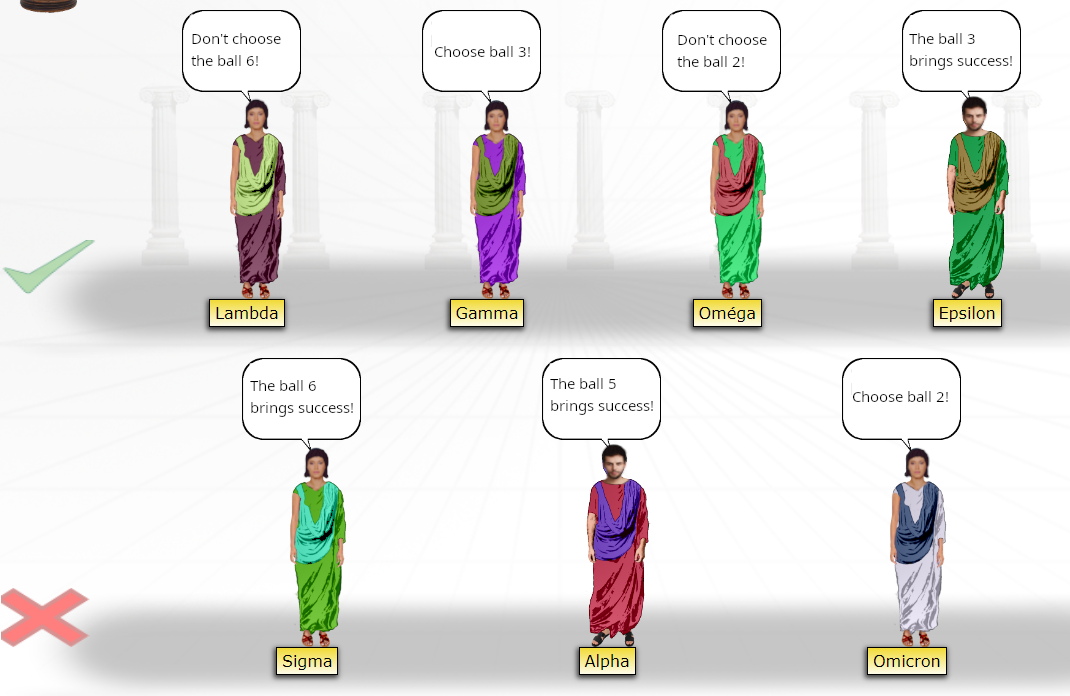
Sometimes the number of the winning ball does not appear directly. You have to eliminate all the losing balls and see that there is only one ball left, which is the winner.

The two liars are Epsilon and Alpha. We cannot therefore choose ball 2, 4, or 1. This leaves ball 3, which is the solution.
Since there’s only one solution, there’s no need to look for other possibilities. Once you’ve found a solution, it’s bound to be the right one!
Number of liars unknown!
The end of the puzzle gets trickier! We know there’s a unique solution, but we don’t know how many liars there are!
So how do we do it?
Consistency, again and again
We’ll have to go through all the possibilities. Fortunately, for an unknown number of liars, there are only a maximum of 4 academicians! For four academicians, there can therefore be 0, 1, 2, 3 or 4 liars.
To determine the number of liars, we need to test, for each number of liars, whether there is a unique solution. If there is no solution, or if there are several, we eliminate the number of liars and move on to the next one.
A simple case to start with

Omega: Ball 2 brings failure.
Alpha: Don’t choose ball 2!
Omicron: Don’t choose ball 2!
Sigma: Don’t choose ball 2!
Let’s take a look at the illustration above. It seems that our academics have agreed: don’t take the No. 2 ball! This is a good sign: the puzzle will be easy.
0 liar
Very interesting situation. Everyone’s telling the truth, so we can’t take ball 2. But we still don’t know which ball to take! With 0 liars, we can see that there are three possible balls – 1, 3 and 4 – which contradicts the introductory statement that only one ball leads to freedom. So, with too many solutions to conclude, we deduce that there is no single solution – as stipulated in the statement. As we are told that there is a unique solution, there are no 0 liars.
1 liar, 2 liars, 3 liars:
None of these cases is possible! Since they’re all saying the same thing… They can only be telling the truth – which is not possible, as we’ve seen – or lying, all together. With these numbers of liars, there’s always a contradiction. But we have to be consistent. I told you the puzzle would be easy!
4 liars: bingo!
They’re all lying. So you have to move everyone to the line ![]() , take ball 2 and drop it in the urn. That’s it!
, take ball 2 and drop it in the urn. That’s it!
A slightly more complex case to continue
Again, academics are talking about the same ball, but this time they don’t agree.

Omega: The ball 3 brings success!
Omicron: Don’t choose the ball 3!
Sigma: Choose the ball 3!
Lambda: The ball 3 brings failure!
Two academics say that one should never take the 3 ball. Two others, on the contrary, claim that one should take it.
Here, at least, it’s easy to find the number of liars! There can only be two, if we want to avoid contradictions. Moreover, liars come in pairs: liars are either Omega and Sigma, or Omicron and Lambda. Any other combination of two liars leads to a contradiction.
Omega and Sigma Liars
If Omega and Sigma are the liars, we know not to choose the 3-ball. Very well, then. But which ball to choose? We can’t be sure. We find ourselves back in the previous situation. There is no single solution. So liars can’t be Omega and Sigma.
Omicron and Lambda Liars: Bingo!
Yes, here they are, the liars! So we know who to move on the line ![]() , and we know we have to place the 3-ball in the urn: it’s the one and only solution to the puzzle.
, and we know we have to place the 3-ball in the urn: it’s the one and only solution to the puzzle.
Another textbook case
Let’s consider the following situation:

Omicron: Ball 1 brings success!
Omega: Ball 2 brings success!
Sigma: Ball 3 brings success!
Epsilon: Ball 4 brings failure!
Here, with a little practice, we see that the solution is 4 liars . Indeed, for this number of liars, there is only one possible solution – take the 4 ball. This is the unique solution required. This is enough to solve the riddle, we don’t need to look any further.
However, let’s see what happens with the other numbers of liars. Just to prove that the enigma is coherent, and above all to discover some interesting cases.
0 liar
Not possible: if everyone tells the truth, there are three balls to choose from when only one is needed.
1 liar
Whatever the liar chooses, there are always several balls to choose from. So no solution is possible.
2 liars
What’s happening here is interesting.
If the two liars are Omicron and Omega, ball 3 should be chosen. The answer is coherent and could be a solution.
If the two liars are Omicron and Sigma, choose ball 2. Here again, the answer is coherent, but it’s a new solution for 2 liars.
If the two liars are Omega and Sigma, choose ball 1. Another coherent answer, but this time it’s a third solution for 2 liars.
We found three solutions for two liars. The other answers, involving Epsilon as one of the two liars, all lead to answers with multiple balls.
So we can rule out the case of two liars, because there could be several solutions – and we know that there must be a single solution.
3 liars
If the three liars are Omicron, Omega, and Sigma, we can no longer choose a ball. The answer is therefore rejected.
Therefore, Epsilon must always be included among the liars. As a result, we obtain answers where there are two balls to choose from. This is not possible because a unique solution is required.
Game or training
By default, the software suggests starting the course in several stages. However, you can practice by choosing the number of academics yourself, in the Parameter Set entry.
Logic and reading
As you can see, the player is active in front of his statement. He must transform certain propositions into their opposite, depending on the number of liars; then he must check the overall coherence of his answer, and test, in the most difficult cases, whether it is unique. Logic here offers students a relevant and fun way of working out a statement without doing any calculations. It’s an excellent preparation for reading mathematical statements, and a great way to develop rigor and logic.
