The examples presented in this article are for three-domino bars, which use numbers greater than 100, which allows us to understand carryover passages.

Of course, we can use fewer dominoes to work on addition. If S is the sum of terms a and b :

• S <= 10: two unit domino bars are enough (there is no carryover so the main point is to move from counting to calculation)
• S<=100: two domino bars – tens+units are enough
• S<=1000: take three hundreds-tens-units domino bars

We won’t go over the technique of moving from tens to hundreds with dominoes again. See the article on counting.

Addition

Addition is commutative: a + b = b + a = S. But this does not mean that there is no order in the operation. There is an order – we have a first element a and a second b , but this order does not matter since the operation is commutative.

But since we have two ordered elements, we will put a in the first bar and b in the second.

Let's perform the following calculation: 347 + 264

So we’ll put a in the top bar and b in the bottom bar:

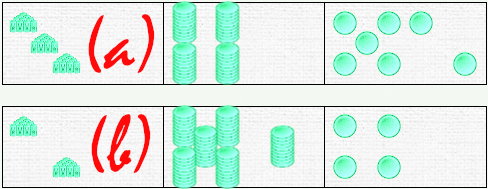
To perform the calculation, all you have to do is pour the contents of one bar into another and rearrange the tokens so that any tens disappear. The result is read from the remaining bar.

Mathematically, this is absolutely correct. But there’s a point to this addition operation. In dominoes, the two initial contents, cardinals a and b, are destroyed in the operation, and the sum S appears on one of the two bars, while the other is emptied. If we wanted to assign a Vergnaud type to the operation, we’d say it’s a transformation operation. But in a transformation, there’s always a direction.

In everyday life, when we perform an addition-transformation, it’s the second element that we add to the first. In a recipe, when you’re asked to add a pinch of salt, you pour it into the pan that already contains the rest of the mixture. Not the other way around. Even if the operation is commutative.

So, we’re going to empty the second bar into the first, and not the other way around, because we want to keep the direction of the operation. The result will therefore be read in the bar that currently contains the value a.

 

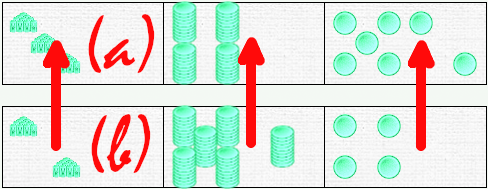
Now let’s look at the hierarchical order of units. Let’s face it: with dominoes, there’s no obligation to use the traditional hierarchical order, i.e. first deal with the units, then the tens, then the hundreds. Give it a try. You’ll see that you can handle the order of the dominoes any way you like. There are just two rules: pour one bar into the other and make the tens crossings.

It couldn’t be simpler. Even so, the domino can be an excellent illustration of addition. I suggest letting students practice as they see fit, so that they can get the hang of it. Be careful: a token is destroyed if placed outside the domino. So aim carefully.

The operations we are used to solving are conventional techniques. In fact, it’s quite possible to change them. Want proof? Here’s an operation performed using a different technique. Here, we could start on the left, the right or in the middle, but the operation would still be the same.

 

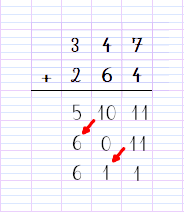
We have indicated the tens’ passages with arrows. Note that this operation cannot be carried out with our dominoes, because 11 cannot appear in the units domino.

Obviously, the “classic” addition operation is taught because it has an advantage over other techniques: it takes up the least space. With two operands, it fits on 4 lines – there’s one line for the carry, two for the operands, and one for the answer.

The column addition with the domino

The column addition is especially useful for numbers greater than 10. For the rest, online calculation and mental calculation are sufficient. The use of dominoes is especially useful for illustrating the classic operating technique with the passage of the carry.

So to begin, let’s be explicit and explain the objective to our students: we are going to learn how to add up, on paper, whith the help of dominoes.

So we’re going to write the addition in columns, following the instructions: put one digit in each box, line up the numbers, leave an empty line above for the carry, and of course a line below for the result. Vocabulary is introduced: “carry”, “result”.

Once the numbers are written on our rough paper, we prepare the domino:

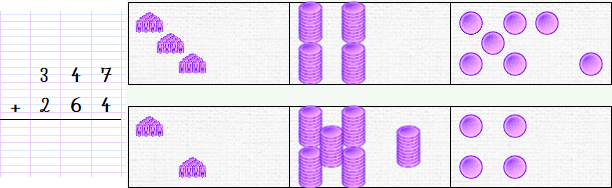
Since we want to learn the conventional technique, we respect the hierarchical order: units, tens, hundreds. So we proceed from right to left.

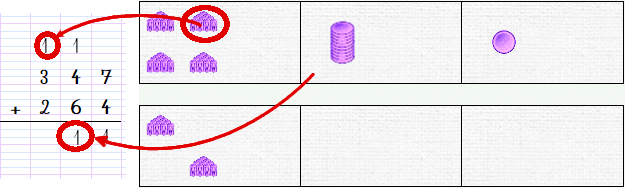
We start by moving the units: we will try to place the 4 tokens from the bottom unit domino into the top unit domino, which already has 7. We can move the first three pieces. When the top domino contains 10 pieces, we can no longer continue. There is one piece left at the bottom.
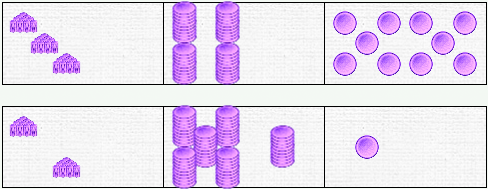If they have already had a little practice, the students already know what to do: the passage! We therefore transfer the 10 pieces from the unit domino to the neighboring domino. Then we move the remaining token from row b to row a :

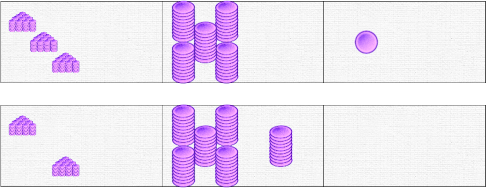
We transfer the operation to paper, indicating the tens added in the carryover line. We indicate the result. This step is important; you should spend a little time explaining it well. Note: the result is read on the top line of the domino, but it is written in the bottom line of our operation.

Let’s start again with the tens. We want to add the bottom tens to the top tens. We can only move 5; that leaves 1.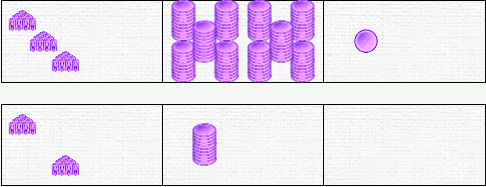

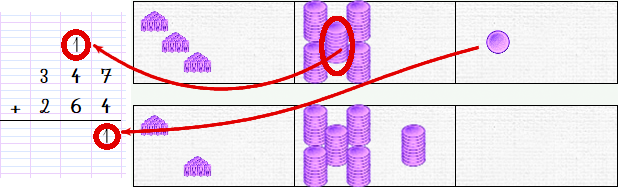
So we make a new transition, from the ten tens to 1 hundred, then we migrate the ten from the bottom to the top. Once this is done, we note the correspondence on our written operation. The hundred is added in the carry line. The number of tens in the top bar is indicated in the second box of the result line.

Finally, we still need to move the remaining two hundreds, and we have the solution: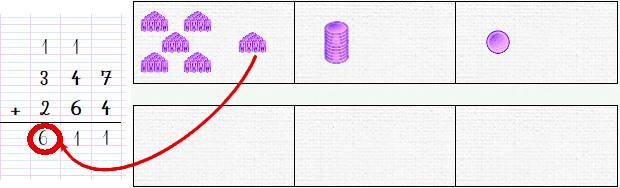

It is important to clearly differentiate between the carry line and the result line: on the carry line, we indicate the number of tens or hundreds that have passed (always 1 if there are two operands) while on the bottom line, the result reflects the contents of the domino.

Why manipulate?

Simply to show that the carry does not come out of a hat. There is nothing magical about it: it is the result of the passage, the transformation of units from the lower hierarchy to the higher hierarchy.

Training

You can train in three steps:

1. initiation : simultaneous work on paper and dominoes, as we have just shown
2. training : first perform the operation on paper, doing the calculations, then check using the dominoes
3. improvement : do without dominoes

Finally, we will address additions with more than two operands, and this necessarily without dominoes.