This post deals only with the “classic” multiplicative bar diagram. Since July 2024, multiplication problems have been enriched by a new model, the Cartesian scheme, which is dealt with in another article.

The multiplication bar diagram allows you to model multiplication and division problems. On Actilud, you’ll find a variety of exercises involving different types of multiplication problems. But before you start solving these problems, a brief introduction to the multiplication “machine” seems necessary.

One possible approach is to repeat the one discussed in my article on the schematization of additive problems. Let’s not forget that the model on the site is not an abstract entity but rather a “virtual machine” that can be easily manipulated.

The multiplicative bar diagram can be used to model multiplication and division problems. On Actilud, you’ll find a wide range of exercises involving different types of multiplicative problems. But before you start solving these problems, you’ll need a little introduction to the multiplicative “machine”.

One possible approach is to take up the one discussed in my article on the diagramming of additive problems. Remember that the model on the site is not an abstract entity, but a “virtual machine” that can be easily manipulated.

 

The ideal, initially, is therefore to present the tool to the students with minimal instructions:

It’s a “problem-solving machine.” Find out how it works.

Why is it called a problem-solving machine?

What kinds of problems can it solve?

Ideally, students will have access to an interactive whiteboard, tablets or computers for their research activities on the site.

Let’s take a closer look at how the machine works.

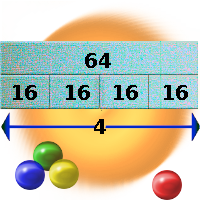
Setting

There are 3 entries in the “Game” menu. The first, “Instructions for use”, is an animated presentation of the machine’s operation – which we’ll cover here, with a few additional pedagogical pointers.

The second entry, “Practice – Problems”, allows you to familiarize yourself with a few simple problems, bearing in mind that a much more complete range of problems can be found in exercise “Multiplication, division with diagrams”.

The third entry, “free use”, is of interest to us here, as it enables us to discover the machine in the first instance, and then work on third-party problems proposed by the teacher.

The “difficulty level” entry, whose content varies according to the game chosen, offers two possibilities, “product up to 100” and “product up to 1000”. These entries allow the user to gauge the difficulty of the calculations and define the limits of the machine. It’s up to the teacher to determine the level of difficulty.

First step: discovery

In our example we will use the 3, 2 configuration. You can use 3, 1 to limit the product to the first hundred.

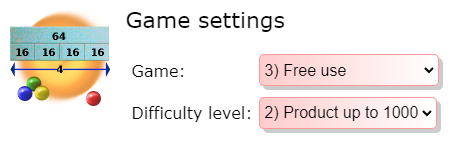
This is what we get on the site: the machine is in its initial state, which corresponds to the operation: 1×1=1 or 1:1=1:

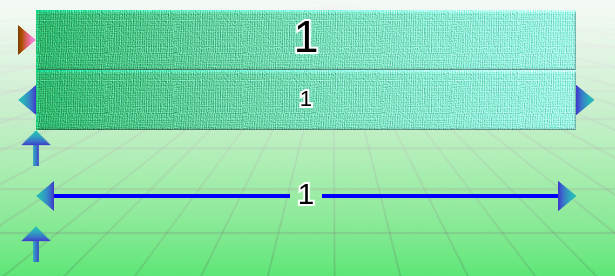
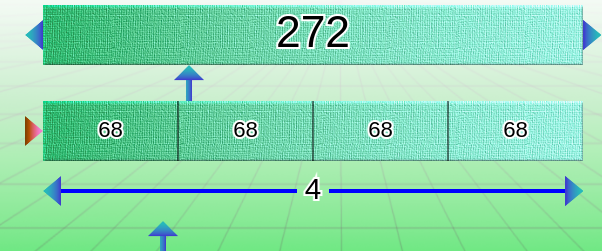
In multiplication, the top bar is the product, the middle bar is the multiplicand, and the bottom bar is the multiplier.
In division, the top bar is the dividend, the middle bar is the integer quotient, and the bottom bar is the divisor.
Of course, these technical terms are for the teacher, not the students—at least not initially!

There are two ways to use the multiplication diagram. This is the role of the red arrow, which we’ll come back to later. To change the numerical value in a bar, click on the arrows at the ends or the move arrow below the bar. Let’s see what this might look like:

 

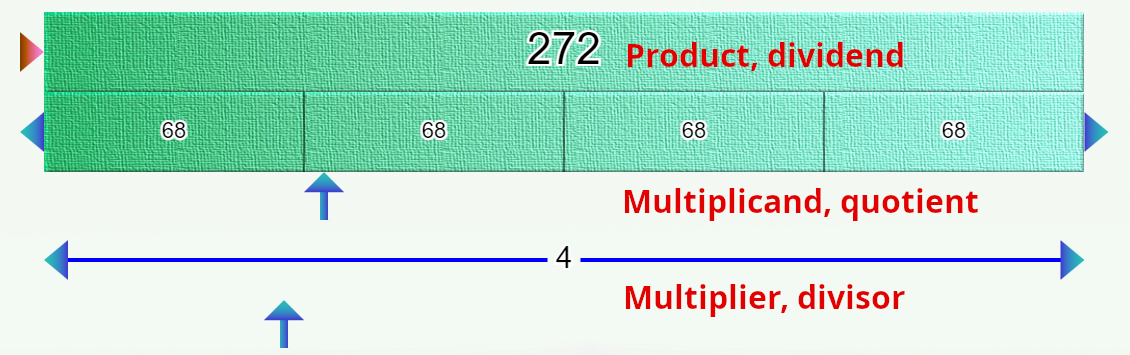
To obtain this result, first use the multiplicand arrows up to value 68: the bottom arrow allows you to move quickly through the bar; the two side arrows allow you to adjust the position to the nearest unit. Do the same with the multiplier bar.

So we have the operation:

272 = 68 x 4 or 68 = 272 : 4 or 4 = 272 : 68 (we use the “:” common in elementary school to signify integer division in a line).

Problematize without delay

To name the bars, technical terms are complicated and risk slowing down the acquisition of an understanding of the model. It’s better to use an analogy; you can start with an example of the distribution of objects in packets of units – take marbles for a concrete example:

The product or dividend bar could become the units bar (number of marbles).
The multiplicand or quotient becomes the size of the packets or the size of the shares
The multiplier or divisor becomes the number of packets or the number of shares

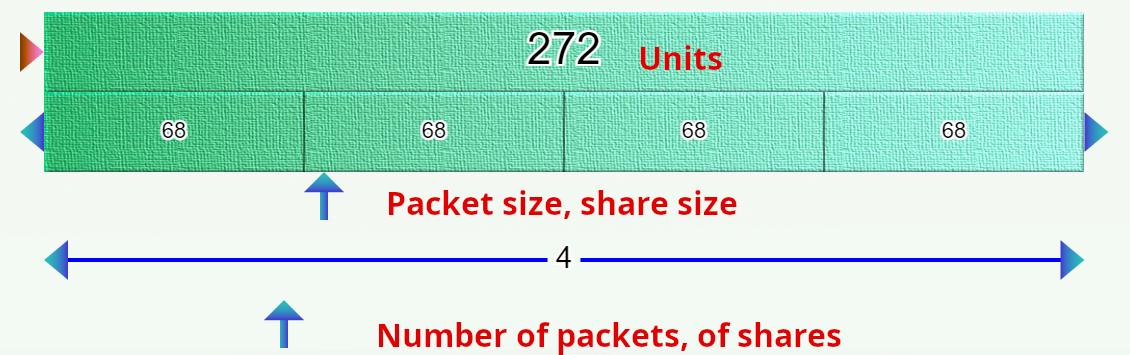
Starting with a given numerical situation, you can ask students to invent situations in which these numbers might be encountered. You can, of course, start with multiplication situations and deal only with those. But thanks to this model, we can quickly invent simple problems involving multiplication or division, based on a single representation:

(a) I have 4 packs of 68 marbles. How many marbles do I have in total?

(b) Alice has 272 marbles. She divides them into 4 equal bundles. How many marbles are in each bundle?

(c) Alice divides her 272 marbles into bundles of 68 marbles. How many bundles does she make?

In case (a) the answer is therefore read on the “number of units” bar. The answer for case (b) is read on the “packet size” bar. Finally, the answer for case (c) is read on the “number of packets” bar.

The question mark to indicate where the answer is

Use the “question mark” label to indicate where the answer bar is located. When you place the label over a bar, the digital display disappears.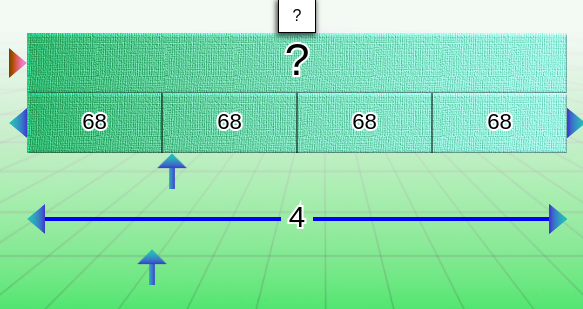

 

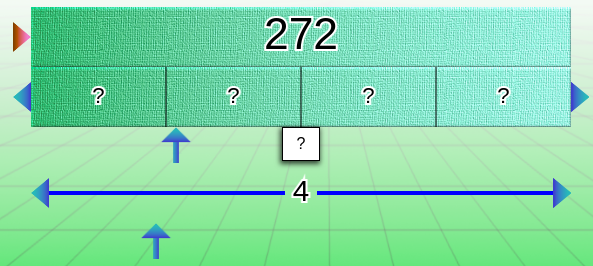
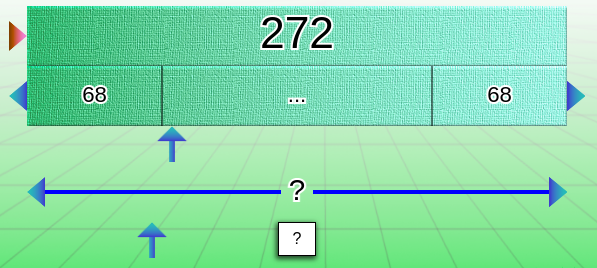
In the latter case, when the question mark is placed on the multiplier/divisor bar, there is an impact on the display of the middle bar, with the appearance of three points “…” (when possible) to prevent students from simply counting the boxes!

The use of the question mark allows students to check that they have understood how the bar works and that they are going to look for the answer in the right place.

Then, by proposing problems with the question mark already positioned on a bar, students will have to find the calculations to be carried out as well as the answer, which will be validated by removing the question mark.

Problems galore

A very stimulating exercise for the students is to leave the machine as we’ve set it up, give them a problem and ask them to model it. Of course, they also have to indicate the bar on which the answer will be read, by positioning the question mark.

In a session, there is a phase of individual research (or in a small group, but be careful to ensure that each pupil manipulates) and a phase of restitution, where the proposed solutions are discussed.

It’s advisable to deal with several problems in one session; don’t dwell on a single statement. Of course, this approach makes more sense if you alternate between problems requiring multiplication and those involving division!

Beware, however, of certain types of statements. Those involving rectangular configurations (such as calculating the area of a rectangle) or Cartesian products (number of combinations, etc.) do not lend themselves well to the semantic interpretation of our bars (number of packets and packet size), since in this case, the data are interchangeable. This type of problem should be avoided in the diagram approach phase.

As you can see, in this mode of operation, you can’t directly enter the product.

A variant for finding divisors and decomposition

That’s the advantage of digital: you can make things a little better. You can also make them more complicated! So it’s up to you to decide whether this option is suitable for your students.

Clicking on the red arrow switches the diagram to a second operating mode, more appropriate when looking for a divisor or a quotient from the dividend.

First, with the up arrow, we indicate the dividend. Then by pressing the down arrow, we can automatically calculate the divisors and quotients (whole numbers obviously).

We arrive at decompositions of the type:

272

= 1 x 272 = 2 x 136 = 4 x 68 = 8 x 34 = 16 x 17

= 17 x 16 = 34 x 8 = 68 x 4 = 136 x 2 = 272 x 1

All this without effort. This allows us to explore the properties of whole numbers, to highlight the commutativity of multiplication since we observe a symmetry in the writings.

Students who are truly comfortable with the model should be given a choice of how it operates.

On-site training

Actilud.com, numeration and basic problems, multiplication, division with diagram

In the settings dialog window you can very finely adjust the difficulty and nature of the work to be done.

Comprehension problems?

If your students have comprehension problems, which is very common, you can focus on a single type of statement. For example, choose “marbles” in the “statement” entry. For this type of statement, you can select multiplication, division quotition or division partition. Once students have solved all three types of operation, you can ask the program to make a random selection, again with the same problem. Obviously, the data will change randomly.

Once you’ve mastered this problem, you can move on to the next.

In the “statements” entry you notice that the problems are followed by a letter, which corresponds to the type of statement:

a: simple multiplication or division problem
b: rectangular configuration (when there is a length and a width)
c: n times more or less
d: Cartesian product

This distinction makes it possible to limit random choices to certain categories in order to improve the progression of learning.

During the training period, you therefore have the opportunity to very finely adapt the learning to each group of students. Since the parameter inputs are always numbered, it is easy to indicate, on the board, the series to be done by their numbers, as we did ourselves in this article:

 

Here the instructions are: H3, 4-3-2-7. Students in this group will only work on the “chocolate” statements, and will have to find and perform the calculations, with products or dividends up to 1000. This is a consolidation phase since the type of problem will be chosen randomly.

Feel free to modify the ideas we’ve outlined here. The Actilud site is not prescriptive, and the proposed exercises can be adapted to your way of working and your class. Take advantage of the site to alternate manipulative research phases with group presentations.