Sudoku allows you to practice spatial organization while respecting the constraint of having unique pieces in each row, column, and region. It’s an excellent exercise in observation, concentration, and logic. It also introduces the concepts of rows and columns, and therefore horizontality and verticality. It’s also a great way to memorize numbers.

Game rules

Sudoku is a square grid containing n x n cells. On Actilud, you can choose between 4×4, 6×6 and 9×9 grids. Each square can contain a sign; on the site, these are either fruits or numbers. The grid is organized into rows, columns and regions, which are rectangular areas containing as many squares as a row or column. A sign can only appear once in each row, column and region. At the start, a certain number of signs are placed in the grid; the task is to complete it, respecting the positional constraint.

A 4×4 Sudoku puzzle with fruit. The fruit in a yellow frame is the puzzle data; it cannot be removed.

Sudokus on Actilud

They are obviously for educational purposes, so they are not particularly difficult! Don’t expect to need advanced techniques to solve them! They are randomly generated by an algorithm that ensures that it is always possible to find a square using the two strategies outlined below.

Concept of candidate

A candidate is the common term for the signs that are likely to be placed in a cell. In the Sudoku above, the bottom right cell has two candidates: the plum and the kiwi. Indeed, these two fruits are not present in the row, column, or region containing this cell. Based on this observation alone, it is not possible to decide for the moment. On the other hand, the cell directly above can only contain one candidate: the strawberry, since the row already contains the other three fruits. The strawberry is therefore the only candidate for this cell: it can be placed.

Two strategies for finding unique candidates

Systematic examination of boxes by counting

This is the basic technique, which I just explained. We observe a box, we look for the signs present in the areas that contain it. If there is only one possible, we place it.

This technique works well on 4×4 or 6×6 grids; but it is quite tedious. It requires observation and a lot of concentration. The more signs there are, the more difficult it is. Paradoxically, it is even more difficult on 9×9 grids with fruit, because when you know the numbers, it is easier to memorize them. If you are a teacher, it might be interesting to test the grids with fruit yourself; you will then be able to better appreciate the difficulty pupils experience when they are asked to use numbers when they barely know them.

The topological technique

It is done by visualizing the areas of their intersection; it gives better results. Students should be encouraged to use it. Let’s take the example above and observe some rows or columns containing the kiwi:

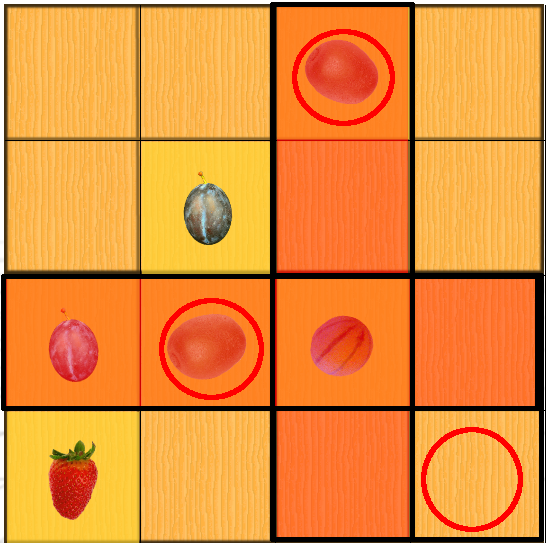
The remaining squares in the row containing the kiwi cannot contain another kiwi; the same goes for the column. In the lower right region, there is only one square left to contain the kiwi: the one marked by an empty circle. Now we can place the kiwi and eliminate the plum, which was a candidate with the previous technique.

The topological technique is therefore based on the intersection between rows, columns, and regions. The minimum, of course, is to use two zones. See what happens with the plum: the intersection of a row and a region is enough to reveal a box:

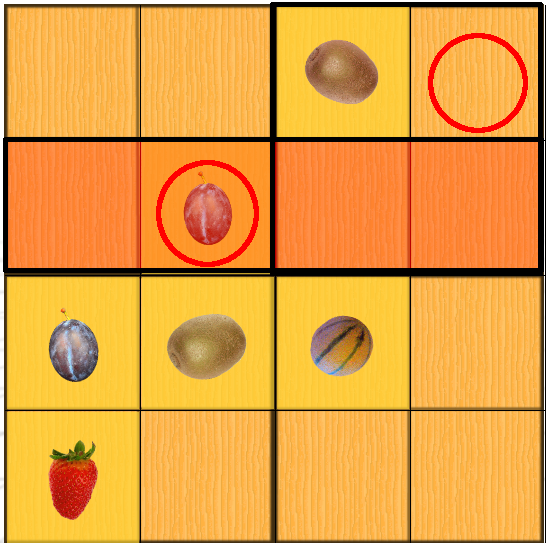Sometimes you need to use multiple rows, columns, or regions to find a square. This is especially true in large grids.

In 9×9 grids, we first look for the most represented signs, as these are the ones with the greatest chance of using our topological technique. To do this, we can count the number of signs and select those that are the most numerous. But we can also rely on our overall perception of the situation. The brain is quite capable of perceiving the most numerous signs without having to count them.

Look at the number 1 in the Sudoku below. We see that two columns, a row and a region form an intersection, highlighting a square that must contain it; whereas if we had used the technique of counting candidates, we would have found two other possible candidates: 4 and 6.

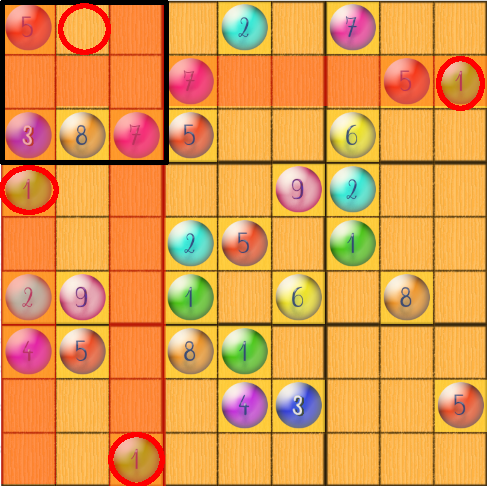In large grids, we start by applying the topological technique; then, if there are still boxes, we use the counting technique – as there are fewer boxes to count, the technique is less tiring!